文章目录
- 131. 分割回文串
- 题目描述
- 回溯代码
131. 分割回文串
题目描述
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2:
输入:s = “a”
输出:[[“a”]]
提示:
- 1 <= s.length <= 16
- s 仅由小写英文字母组成
回溯代码
在此代码片段中,子字符串是通过递归函数 backtracking 来获取的。函数 backtracking 是一个回溯算法的实现,用于找到字符串 s 的所有可能的回文分割。回文分割是指将字符串分割成若干子串,使得每个子串都是回文的。
下面是 backtracking 函数在寻找子串时的详细过程:
-
函数 backtracking 接收原始字符串 s 和一个 startIndex 参数,该参数指示当前考虑的子串的起始位置。
-
在每一层递归中,函数通过循环从 startIndex 遍历到字符串 s 的末尾。
-
在每次迭代中,它通过调用 isPalindrome 函数来检查当前考虑的子串 s[startIndex, i] 是否是回文。
-
如果检测到子串是回文,使用 substr 方法从 s 中提取出回文子串。substr 方法的第一个参数是子串的起始位置,第二个参数是要提取的字符数。这里,提取的字符数计算为 i - startIndex + 1,表示从 startIndex 到 i(包含 i)的子串长度。
-
获取到的回文子串 str 被加入到临时路径 path 中。
-
然后,递归调用 backtracking 函数,在寻找剩余子串的新的回文分割方案,此时 startIndex 更新为 i + 1,因为 i 位置的字符已经包含在了当前找到的回文子串内。
-
递归返回后,执行 path.pop_back(),这是回溯的一部分,它将最后一个添加到 path 中的回文子串移除,以便 path 可以用于下一次循环迭代时的新的分割方案。
-
当 startIndex 大于或等于字符串 s 的长度时,意味着已经到达字符串的末尾,当前 path 中存储的回文子串序列即为 s 的一个有效分割,此时将 path 加入到 result 中。
通过这种方法,代码实现了在递归循环中对字符串进行子串的分割,并确保了每个分割方案中的所有子串都是回文的。
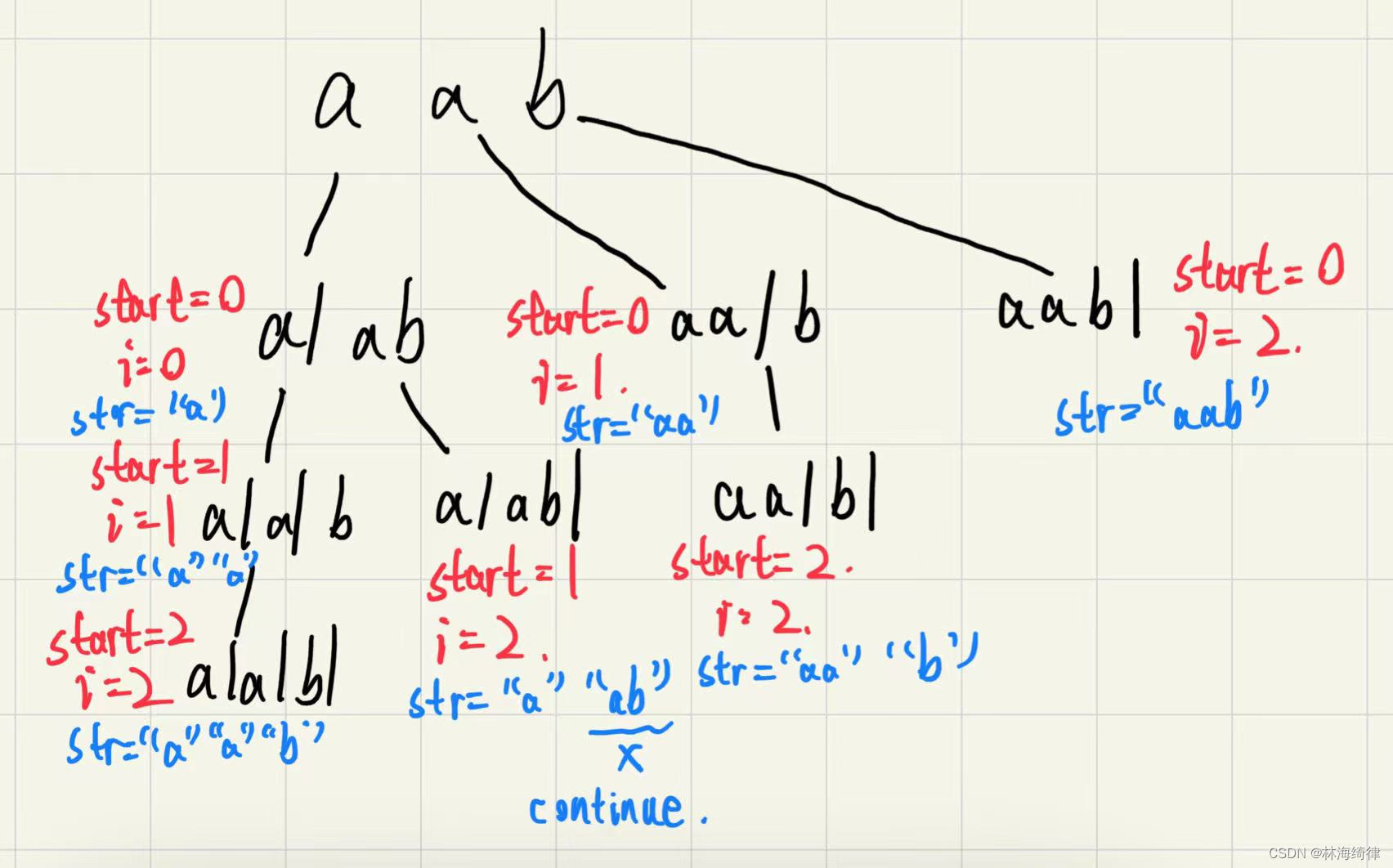
假设我们有一个字符串 s = “aab” 并且我们想要找到所有可能的回文分割方案。下面是 backtracking 函数在这个字符串上操作的示例:
-
初始调用
backtracking("aab", 0),startIndex是 0,意味着我们从字符串的第一个字符开始。 -
第一层递归的循环从
i = 0开始:a. 检查子串
s[0, 0]即"a"是否是回文 — 是,所以path变为["a"]。b. 递归调用
backtracking("aab", 1)查看从第二个字符开始的所有回文分割方案。 -
第二层递归开始,现在考虑的子串是
"ab":a. 循环从
i = 1开始,检查子串s[1, 1]即"a"是否是回文 — 是,所以现在path变为["a", "a"]。b. 递归调用
backtracking("aab", 2)查看从第三个字符开始的所有回文分割方案。 -
第三层递归开始,现在考虑的子串是
"b":a. 循环从
i = 2开始,检查子串s[2, 2]即"b"是否是回文 — 是,所以现在path变为["a", "a", "b"]。b. 递归调用
backtracking("aab", 3),发现startIndex等于字符串长度,意味着找到了完整的一组分割方案。将其添加到result中,result = [["a", "a", "b"]]。c. 回溯发生,
path.pop_back()移除最后一个元素"b",现在path = ["a", "a"]。 -
返回到第二层递归,继续
i的循环,现在i = 2:a. 检查子串
s[1, 2]即"ab"是否是回文 — 不是,所以不改变path。b. 循环结束,开始回溯,
path.pop_back()移除最后一个元素"a",现在path = ["a"]。 -
返回到第一层递归,继续
i的循环,下一次i = 1:a. 检查子串
s[0, 1]即"aa"是否是回文 — 是,所以path变为["aa"]。b. 递归调用
backtracking("aab", 2)查看从第三个字符开始的所有回文分割方案。 -
第四层递归开始,现在考虑的子串是
"b":a. 循环从
i = 2开始,检查子串s[2, 2]即"b"是否是回文 — 是,所以path变为["aa", "b"]。b. 递归调用
backtracking("aab", 3),发现startIndex等于字符串长度,意味着找到了另外一个完整的一组分割方案。将其添加到result中,现在result = [["a", "a", "b"], ["aa", "b"]]。 -
回溯发生,
path.pop_back()移除"b",回到path = ["aa"]。然后第四层递归的循环结束,path.pop_back()再次移除"aa",回到path = []。
最终的 result 包含了所有可能的回文分割方案:[["a", "a", "b"], ["aa", "b"]]。这样,我们就逐步构建了每一个可能的回文分割方案并将有效的方案添加到结果集中。
class Solution {
public:
// 主函数,调用回溯函数并返回结果
vector<vector<string>> partition(string s) {
backstracking(s,0); // 从字符串的第一个字符开始进行回溯
return result; // 返回所有可能的分割方案
}
private:
vector<vector<string>> result; // 存储所有可能的分割方案
vector<string> path; // 用于存储当前的分割方案
// 检查一个子串是否是回文串
bool cheak(string& s,int begin,int end) {
for(int i=begin,j=end;i<j;i++,j--) // 从两头开始向中间检查
if(s[i]!=s[j]) // 如果两头字符不相等,则不是回文
return false; // 返回 false
return true; // 所有字符都相等,返回 true
}
// 回溯函数
void backstracking(string& s,int start) {
if(start==s.size()) { // 如果 start 等于字符串的长度,表示已经处理完毕
result.push_back(path); // 将当前的分割方案添加到结果中
return ; // 返回上一层
}
// 从 start 开始往后查找可能的分割点
for(int i=start;i<s.size();i++) {
if(cheak(s,start,i)) { // 检查从 start 到 i 的子串是否是回文
string str=s.substr(start,i-start+1); // 是,将其作为一个分割
path.push_back(str); // 将子串添加到当前的分割方案中
} else {
continue; // 如果不是回文,跳过当前的字符,继续下一轮循环
}
backstracking(s,i+1); // 递归调用,从下一个字符开始继续分割剩余的字符串
path.pop_back(); // 回溯,移除最后添加的子串,尝试其他可能的分割点
}
}
};