• 🙋‍♂️ 作者：海码007
• 📜 专栏：计算机四大基础专栏
• 📜 其他章节：网络快速入门系列、计网概述、计网应用层详解、计网Web和HTTP、计网FTP、计网EMail、计网DNS、计网P2P
• 💥 标题：【数据结构和算法 二叉树】根据前序、中序、后序来确定一颗二叉树
• ❣️ 寄语：不怕苦，吃苦半辈子。怕吃苦，吃苦一辈子！
• 🎈 最后：文章作者技术和水平有限，如果文中出现错误，希望大家能指正

0 引言

最近在学习数据结构和算法，学习到二叉树。自己找到了如何根据前序、中序、后序来确定一颗二叉树结构的快速方法，今天分享出来。

首先了解一下二叉树的递归特性，一颗二叉树把根节点去掉，然后你又可以得到两颗二叉树。以此类推都是二叉树。

• 前序遍历：首先是输出根节点的数值，然后再是左节点、右节点。所以根据前序遍历可以很容易找到一棵树的根节点，也就是最左侧的数值就是一颗二叉树的根节点。
  • 例如：前序遍历 ABCDEF ，那么可以知道A就是一棵树的跟节点
• 中序遍历：首先输出的是没有左子树的节点，然后再是自己，然后再输出右子树节点。所以根据中序遍历以及一棵树的根节点可以很容易确定其他节点是左子树还是右子树。
  • 例如：还是和上面同一颗树，中序遍历是CBAEDF，那么根据刚才的前序遍历可以知道A是根节点，那么CB是属于左子树的，EDF是属于右子树的。
• 后序遍历：首先输出的是左右子树值都输出过的节点，或者是没有左右子树的节点。类似前序遍历，后序遍历可以很快找到树的根节点，也就是最右侧的数值。

1 确定二叉树结构的方式

1.1 前序和中序

前序：ABCDEF
中序：CBAEDF

1. 根据前序可知 A 为根节点
2. 然后知道根节点后，再根据中序可以知道 CB 属于左子树， EDF属于右子树。
3. 然后我们按照递归的思想，将 CB 看作一颗需要重新确定结构的二叉树， EDF 也看作一颗新的二叉树。
4. 然后根据 BC 的前序顺序可知， B 是树的根节点。然后 根据 CB 的中序顺序可知，C是左子树的节点。
5. 同理根据 DEF 的前序顺序可知，D是树的根节点。然后根据 EDF 的中序顺序可知，E是左子树，F是右子树。

总结：思想就是把一颗二叉树划分开来，然后从最小的二叉树慢慢确定结构，然后再整合成一颗大的二叉树。

1.2 后序和中序

后序：BDCAFGE
中序：ABCDEFG

1. 同理先找到根节点，后序顺序的最右侧就是根节点 E。
2. 然后根据中序顺序将这颗二叉树，划分成左右子树。左子树：ABCD，右子树：FG。
3. 然后找到左子树的根节点，左子树后序顺序是BDCA，那么根节点为 A。然后根据中序顺序ABCD得知，BCD组成了一颗新的右子树。然后同理先根据后序找到根节点，再根据中序判断左右子树。
4. 右子树：FG同理，确定根为G，那么F为G的左子树。

1.3 前序和后序：无法确定结构

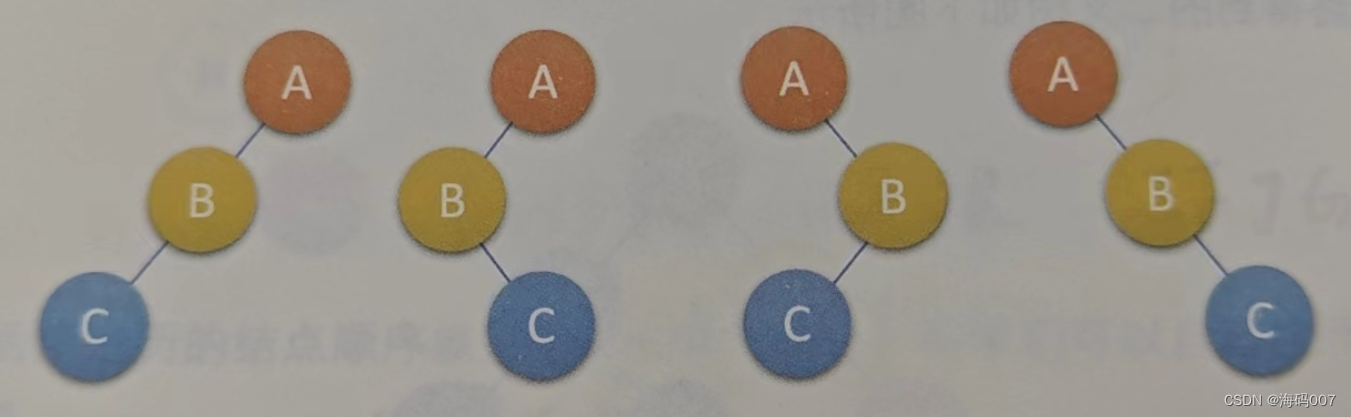
前序：ABC
后序：CBA

根据前序和后序，我们只能确定根节点，但是确定不了左右子树。前序和后序类似。