Multimodal Instruction Tuning with Conditional Mixture of LoRA

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

目录

0. 摘要

3. 任务干扰在多模态指令调优中的 LoRA 应用

3.1 背景：LoRA

3.2 调查多模态指导调优中的任务干扰

4. 条件 LoRA 混合

4.1 动态因子选择

4.1.1 独立因子选择

4.1.2 条件因子选择

4.1.3 动态自适应矩阵的重建

5. 实验

---

0. 摘要

多模态大型语言模型（MLLMs）在不同领域的各种任务中展现了出色的熟练性，越来越关注提高它们在看不见的多模态任务上的 zero-shot 泛化能力。多模态指令调优已成为通过指令在各种多模态任务上对预训练模型进行微调以实现 zero-shot 泛化的成功策略。随着 MLLMs 的复杂性和规模的增加，对于像低秩适应（Low-Rank Adaption，LoRA）这样的参数高效的微调方法的需求变得至关重要，该方法通过使用最小的参数集进行微调。

然而，在多模态指令调优中应用 LoRA 面临任务干扰的挑战，这导致性能下降，尤其是在处理广泛的多模态任务时。为了解决这个问题，本文介绍了一种新方法，将多模态指令调优与条件 LoRA 混合（Mixture-of-LoRA，MixLoRA）相结合。它通过动态构建适应于每个输入实例独特需求的低秩适应矩阵，来减轻任务干扰。对各种多模态评估数据集的实验证明，MixLoRA 不仅在相同或更高秩的情况下胜过传统的 LoRA，展示了其在各种多模态任务中的功效和适应性。

3. 任务干扰在多模态指令调优中的 LoRA 应用

3.1 背景：LoRA

3.2 调查多模态指导调优中的任务干扰

我们的研究深入探讨了在参数高效的多模态指令调优中分析任务对之间梯度方向冲突的任务干扰。对于每一对任务 i 和 j，我们首先估计在根据任务 j 的损失 Lj 优化共享参数 θ 时，任务 i 的损失 Li 的变化，遵循（Zhu等，2022）：

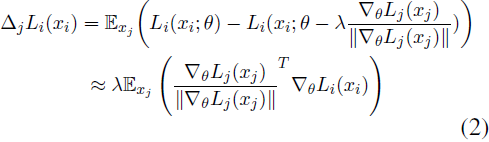
其中，xi 和 xj 是任务 i 和 j 的采样训练 batch，λ 是学习率。然后，任务 j 对任务 i 的干扰被量化如下：

在这里，正的 I_(i,j)​ 表明任务 i 和 j 之间的梯度方向是对齐的，而负值意味着梯度方向是分离的，表明任务 j 对任务 i 产生不利影响。

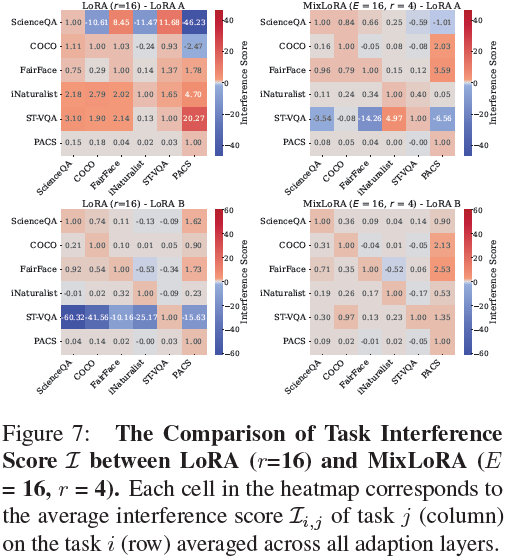
我们在使用 LoRA 和秩为 4 进行微调的 LLaVa（Liu等，2023）模型上进行实验，计算来自 Vision-Flan（Xu等，2023a）的六个不同任务之间的任务干扰，包括 “ScienceQA”（Lu等，2022）（用于“复杂推理”），“COCO”（Lin等，2014）（用于“粗粒度感知”），“Fair-Face”（Karkkainen和Joo，2021）（用于“细粒度感知”），“iNaturalist”（Van Horn等，2018）（用于“知识密集型”），“STVQA”（Biten等，2019）（用于“OCR”），以及 “PACS”（Li等，2017）（用于“领域特定”）。

我们基于涉及 LoRA A 和 B 的梯度计算任务干扰矩阵 I 的平均值，跨越各个层次。图 2 显示了 MLP（图 2a） 和 Self-Attention（图 2b） 在第 5 层和第 25 层 Transformer 层的 LoRA A 和 B 的任务干扰分数。

我们的结果显示，对于 LoRA A 和 B，无论在浅层还是深层 Transformer 层，都存在显著的任务干扰。例如，如图 2b 所示，在第 5 层的 LoRA A 中，领域特定的分类任务 “PACS” 对粗粒度感知任务 “COCO” 产生负面影响，负干扰分数为 -7.3。与此同时，还观察到了正面的影响。例如，图 2a 显示，在 LoRA B 的第 5 层，“PACS” 对 OCR 任务 “ST-VQA” 产生积极影响。正面和负面干扰的存在表明指导任务之间存在复杂的动态：正分数（红色）表明一个任务的学习可以增强另一个任务的性能，而负分数（蓝色）则意味着一个任务的学习可能会妨碍另一个任务。这些发现突显了在参数高效的多模态指导调优中存在显著的任务干扰，并强调了需要有效的适应方法来确保在各种多模态任务中具有强大和多功能的性能。

4. 条件 LoRA 混合

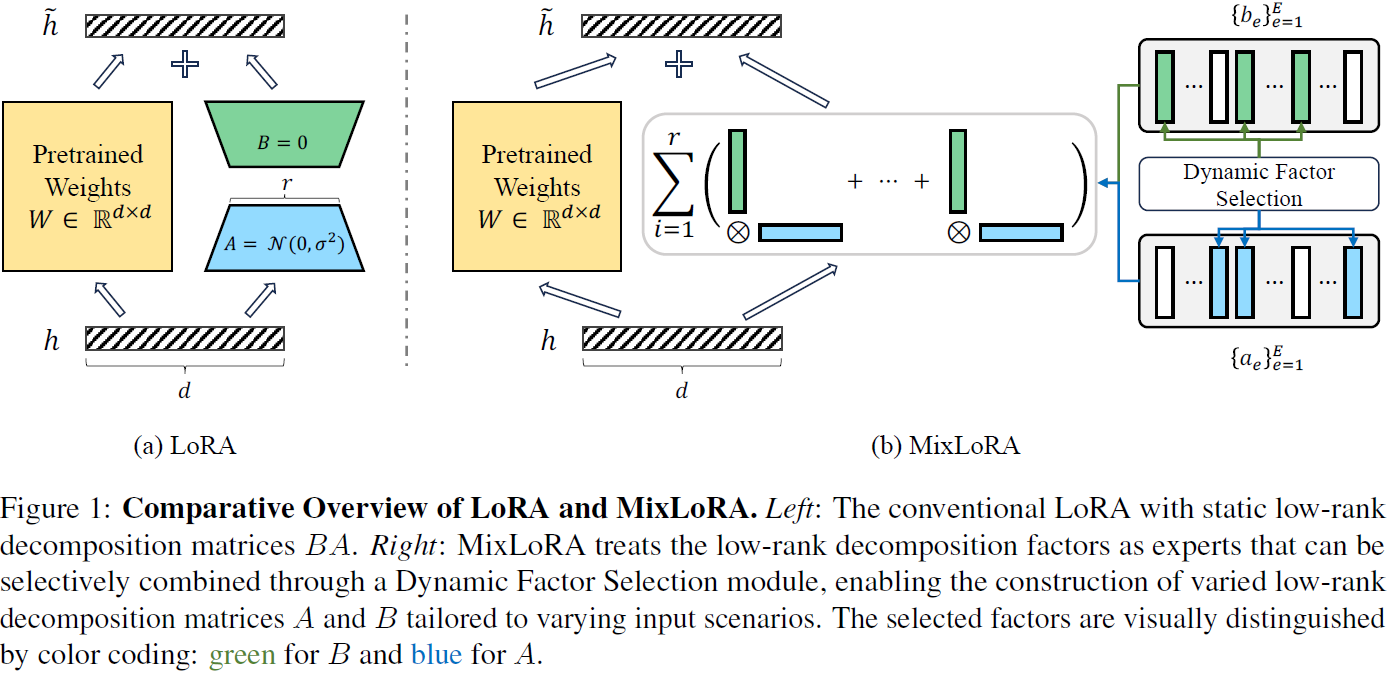
受到 “专家混合” 概念的启发（Shazeer等，2016），我们提出了条件 LoRA 混合（MixLoRA），它利用低秩分解因子（low-rank decomposition factors）作为动态选择的专家，构建针对特定输入实例的定制分解矩阵 A 和 B。MixLoRA 促进了对不同输入实例的动态处理路径，从而增强了处理各种复杂多模态指导任务的效力。

条件LoRA混合的核心在于通过张量分解表示权重调整矩阵 ΔW：

其中 {ai, bi} 是 ΔW 的秩 r 分解因子，ai ∈ R^(d_in × 1)，bi ∈ R^(d_out × 1)。

利用 ΔW 可以表示为低秩分解因子 ai 和 bi 外积之和的概念，MixLoRA 引入了一个动态因子选择（Dynamic Factor Selection）模块。该模块通过从扩展的分解因子池

中选择 r 个适当的因子，动态构建特定输入的唯一 ΔW，如图 1（b）所示。

4.1 动态因子选择

动态因子选择模块使用两个主要组件来动态构建 LoRA A 和 B。首先，两个独立因子选择（Independent Factor Selection，IFS）路由器（第 4.1.1 节）分别选择 r 个相关因子，形成适应矩阵 LoRA A 和 B，确保精确、针对实例的自适应。其次，一个条件因子选择（Conditional Factor Selection，CFS）路由器（第 4.1.2 节）通过在选择 LoRA B 时将选择 B 的因子以选择 LoRA A 的因子为条件，推动了一致的自适应过程。

4.1.1 独立因子选择

MixLoRA 采用两个独立因子选择（IFS）路由器，

分别选择 LoRA A 和 B 的 r 个相关因子，如图 3 所示。

IFS 路由器采用基于实例的路由方法，相对于基于传统输入 token 的路由，这更具内存效率，用于选择 r 个分解因子。路由策略可以表示为：

其中 Avg(·) 对前一层的隐藏状态 h ∈ R^(seq × d_in) 在序列维度上进行平均。

因子选择过程涉及计算向量 gA∈R^E 和 gB∈R^E，以选择从集合 {a_e​}^E_(e=1​) 和 {a_e​}^E_(e=1​)​ 中的特定子集，分别用于 LoRA A 和 B。为了计算 gA，输入

通过具有权重 W_A ∈ R_(E × d_in) 的稠密层（dense layer）进行处理，然后进行 softmax 归一化和 top-r 选择：

该过程确保选择 LoRA A 的 r 个因子，其中 g_A[i] = 1 表示选择因子 i。相同的过程应用于确定 LoRA B 的 gB。

4.1.2 条件因子选择

尽管到目前为止 LoRA A 和 B 的因子是独立选择的，但我们假设 LoRA A 和 B 的选择之间存在相互依赖关系，可以利用这种关系提高模型的整体适应性和性能。为了利用这种关系，我们提出了一种条件因子选择（Conditional Factor Selection，CFS）策略，其中 LoRA B 投影上权重的因子选择也受到了为 LoRA A 投影下权重选择的因子的影响。

通过 IFS 路由器，LoRA A 从选择的分解因子中组装而成，表示为 A = [a1, · · · , ar]ᵀ，其中 A ∈ ℝ^(r x d_in)。在这之后，CFS 路由器采用权重张量 W_AB ∈ ℝ^(r x d_in x E)，将 A 中的每个因子 A[i] ∈ ℝ^(r x d_in) 映射到专家维度 𝔼。对于每个因子 A[i]，通过 softmax 归一化并在 r 个因子上聚合的映射过程如下：

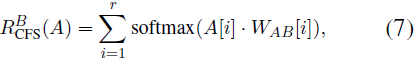
其中 W_AB[i] ∈ ℝ^(d_in x E) 是与 A[i] 相关的映射矩阵。

LoRA B 的因子选择集成了 IFS RB IFS(·) 和 CFS RB CFS(·) 路由器的输出，通过后融合（late fusion）策略形成选择向量 gB，具体如下：

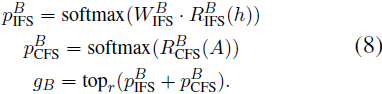
最终选择向量 gB 由来自 IFS 和 CFS 路由器的概率分布 p^B_IFS 和 p^B_CFS 组合而成。这种 CFS 策略使得 LoRA B 的选择能够受到为 LoRA A 选择的因子的启发，促使一个更具连贯性的选择过程。

4.1.3 动态自适应矩阵的重建

最后，MixLoRA 通过利用因子选择向量 gA 和 gB，收集已选因子 aₖ、bₖ ∈ 𝕂，|𝕂| = r，以组装 LoRA A 和 B 的最终矩阵，从而构建动态自适应矩阵。因此，在每次前向传递中，基于这些已选择的因子动态计算权重调整矩阵 ΔW ∈ ℝᵈₒᵤₜ×ᵈᵢₙ，表示为：

5. 实验