前言
在本系列的上两篇文章分别介绍了两种O(n2)的排序算法——选择排序和冒泡排序,今天是第三种O(n2)的排序算法:插入排序。
插入排序
核心思想
它的基本思想是将一个记录插入到已经排好序的有序表中,从而产生一个新的、记录数增 1 的有序表。
在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
换句话说,插入排序是从最少元素的有序数列开始,将新的元素插入到该有序数列中某个位置,使插入后的数列依然保持有序。
这里,最少元素的有序数列其实指的就是只包含一个元素的数列,也就是 arr[0]。
知道这个概念后,再去理解插入排序的思想就容易多了。
假设要对数组 arr[8] = {7,6,9,3,1,5,2,4} 排序,使排序后保持升序有序,那么插入排序的做法是首先划定第一个有序子序列,也就是arr[0~0];
- i = 0, 此时只有一个元素arr[0],已经有序,故当前有序子序列为 arr[0~0]
- i = 1,有序子序列为 arr[0~0],此时将 arr[1] 插入到该子序列中,并保持升序有序,所以arr[1] 被插入到 arr[0] 的前面;此时有序子序列为 arr[0~1] = {6, 7}
- i = 2, 有序子序列为 arr[0~1],此时将 arr[2] 插入该子序列中,并保持升序有序,所以 arr[2] 被插入到 arr[1] 的后面(也就是不做操作)。此时有有序子序列为 arr[0~2] = {6, 7, 9}
- … 中间的过程都是类似的,这里省略
- i = 7 时,有序子序列为 arr[0~6] = {1,2,3,5,6,7,9},此时将 arr[7] 插入该子序列中,并保持升序有序,arr[7] 的新位置应该是当前 arr[3] = 5 的位置,所以这一步要将 arr[7] 正确放到 arr[3]的位置,这个步骤是插入排序中的插入,接下来要详细说明如何将 arr[7] 正确放到 arr[3] 的位置,然后使新的子序列升序有序。
将 arr[7] 正确的插入到有序子序列 {1,2,3,5,6,7,9} 中,总共分为找到插入位置 + 执行插入操作两步。
- 找到插入位置
遍历当前子序列,找到比arr[7]大的第一个元素,该元素的位置就是arr[7]要插入的位置,这里插入位置是arr[3]。 - 执行插入操作
首先用tmp记录arr[7]的元素值,然后将arr[6 ~ 3]依次向右移动一个位置,也就是arr[6 ~ 3] --> arr[7 ~ 4];最后将tmp的值放入arr[3]就完成了插入操作。
/* 插入一个元素到有序子序列 */
// i 的位置是当前要加入有序子序列的元素所在位置
for (int j = 0; j < i; ++j) { // 遍历有序子序列
if (arr[j] >= arr[i]) { // 找到插入位置,第一个 >= arr[i] 的元素,插入位置为 j
// 执行插入操作
int tmp = arr[i]; // 暂存 arr[i] 的值
for (int k = i-1; k >= j; --k) { // 移动 arr[i-1 ~ j] 的元素 --> arr[i, j+1]
arr[k] = arr[k-1];
}
arr[k] = tmp; // 将暂存的原 arr[i] 的值插入到目标位置
}
}
图例
- 第一轮:从第二位置的 6 开始比较,比前面 7 小,交换位置。
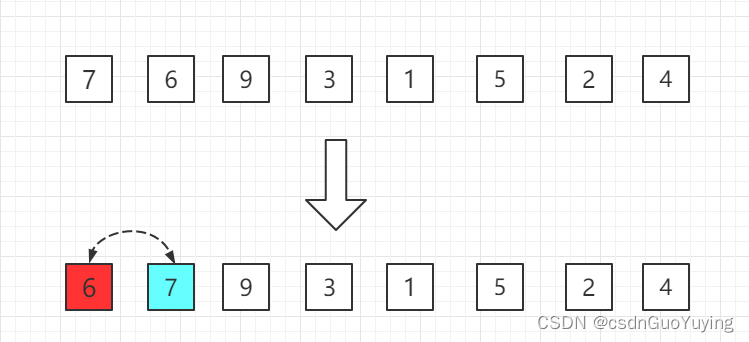
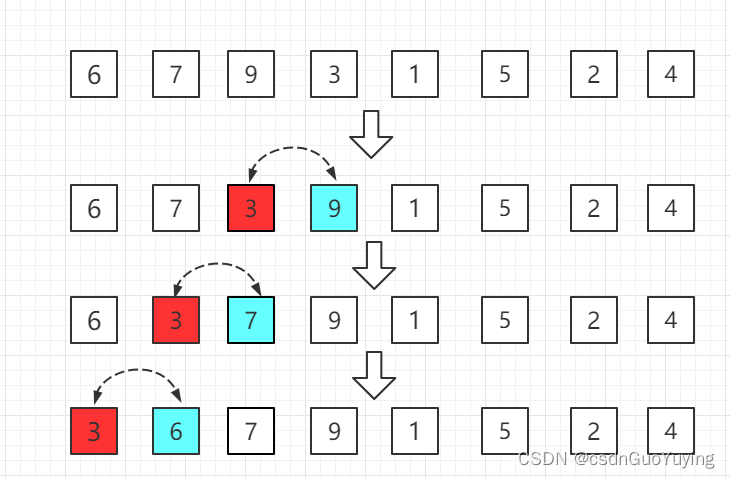
- 第二轮:第三位置的 9 比前一位置的 7 大,无需交换位置。

- 第三轮:第四位置的 3 比前一位置的 9 小交换位置,依次往前比较。
- 第四轮:第五位置的 1 比前一位置的 9 小,交换位置,再依次往前比较。
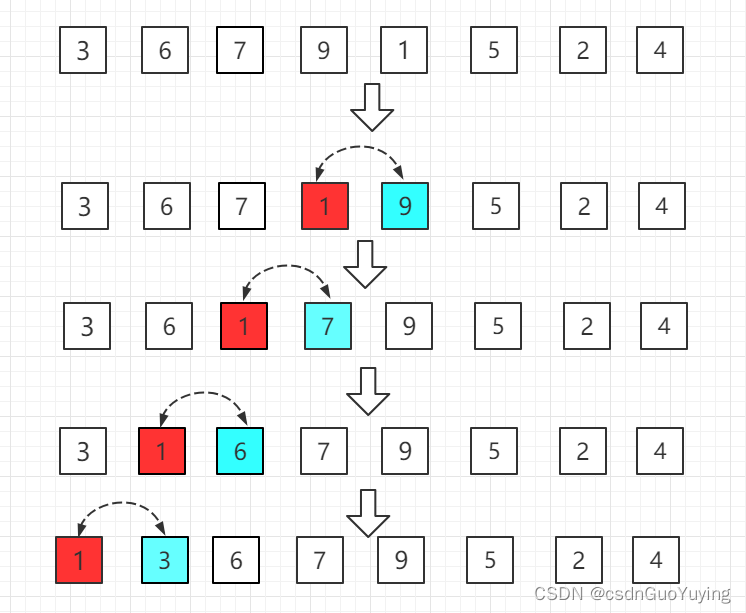
…
就这样依次比较到最后一个元素。
代码
/* 插入排序 */
void insertionSort(int arr[], int len){
for (int i = 1; i < len; i++){
int key = arr[i];
int j = i-1;
while((j >= 0) && (arr[j] > key)) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}
这里演示了插入的另一种实现。思路还是找位置 + 插入。
但之前实现的代码,插入的操作就是一个两层的循环,如果再加上外层的遍历一共需要三层循环,想想看,如何能将两层循环的插入操作合并为一层呢?
直接使 k = i-1, 从 arr[j] 开始,依次执行 arr[j] = arr[j-1] ,直到 arr[j] > arr[i] 即可。