引子

贺新郎·读史
人猿相揖别。只几个石头磨过⑴，小儿时节。铜铁炉中翻火焰⑵，为问何时猜得？不过几千寒热⑶。人世难逢开口笑⑷，上疆场彼此弯弓月。流遍了，郊原血。
一篇读罢头飞雪，但记得斑斑点点，几行陈迹。五帝三皇神圣事⑸，骗了无涯过客。有多少风流人物？盗跖庄屩流誉后⑹，更陈王奋起挥黄钺。歌未竟，东方白。

一部数学发展史，既是英雄人物的灵感迸发史，也是劳动人民艰难的求索史、采矿史。
通往数学顶峰的路崎岖坎坷，无数艰难险阻横亘其间，只有极少数攀登者能登顶，从而领略数学大山的全貌。大部分人因为枯燥的教学，不合适的学习路径而早早放弃了攀登。

数学本来很有趣味，是数学老师把它讲糟了! 但能不讲糟的老师又有几人呢？

代数，几何与分析

代数、几何和分析，成为数学的三大分支。当然还有很多划分法和叫法。

代数和几何都是研究各种数学构造，例如代数里的四元数，几何里的黎曼面，都是经典的数学构造。

代数是什么？代数是研究数的各种运算，这个数，可以是具体的整数、有理数无理数，也可以是矩阵和张量，甚至是更抽象的东西，这种抽象的东西我们就直接用字母替代具体的数，所以叫代数。只要它们符合相同的运算规律，具备相同的结构，我们就可以把它们统一成同一种代数结构。主要的代数结构有：群、环、体、域、模。现代代数的两大主题是结构和表示论。

几何又是什么呢？在初等数学里，它是研究点、线、面、体形状和位置关系的学问，但这可能没有揭示它的本质。按照F.Klein的Erlangen纲领的观点，几何学研究的对象是空间在某个变换群作用之下的不变性质。

微积分，已经渗透到数学的各个领域。可以说”无微积，不数学“。任何一门数学分支，一旦披上微积分的面纱，就变得庄严肃穆，凛然高大起来。微积分，就是拿着放大镜，去研究各种数学构造的微观部分。微分，就是求无穷小量，积分，就是对无穷小进行求和。要求和，就得定义无穷小的度量，有了各种度量，就有了各种曲率。

而要想精确的描述各种数学概念，就先得有集合这门语言，集合是构建整个数学大厦的基础材料。集合上定义距离，就有了邻域，有了拓扑空间，有了流形和纤维丛；集合上定义运算，就有了群，有了变换。集合和集合之间定义映射，就有了同态、同构、同胚。

加法是平移，乘法是伸缩，两者叠加就成了线性变换。矩阵，就是用来表示运动和变换的工具。线性变换就是从一个线性空间到另一个线性空间的、且保持运算的映射。

我们看到的世界，往往只是数学一般规律中的一个特例，或者说，只是偏微分方程的一个特解。例如，连续一定可微吗？可微一定可积吗？连续可微和连续不可微，哪个更普遍？幂、指、对、三角以及它们的复合都是初等函数，也是我们平常多见的函数，但谁能想到，非初等函数才是常态呢？

代数和几何的融合成为代数几何学，它与其他许多学科都有着密切的联系，如拓扑学，微分几何，复几何，分析，代数，数论等，并且在现代理论物理中也有重要的应用，被Atiyah（阿蒂亚）称为 21世纪的三大数学理论的算术几何更是与代数几何息息相关，抽象代数几何学必将在21世纪得到更进一步的发展，继续成为21世纪的主流数学领域。

数学之美

数学原本是美的，是老师和教材让它变枯燥了。老师不激发学生兴趣，不讲问题背景，不讲数学家思考过程，不讲来龙去脉。教材只是抄袭和东拼西凑，或者只浓缩数学家的结果，不交代物理背景，把本来有趣的数学发现变成了干瘪的条条框框，营养成分都被破坏掉了。其实，教学最重要的是引导，而不是灌输。学生感兴趣了，自然会自己求索，自己去找资料，弄明白问题的答案。

数学之美，在于抽象。数学问题是对实际问题的抽象和提炼，是对实际的建模和升华。
不能为了抽象而抽象，而是需要有具体的问题背景做依托，以此为出发点的抽象才是有意义的抽象，才有成效性，才能用来解决更加困难的问题。能解决具体问题的抽象才是好的抽象，才是有意义的，为抽象而抽象的工作最终将被人们遗弃。

数学之美，在于深刻。一个偏微分方程，胜过千言万语。

数学之美，在于严谨。为何《几何原本》至今都保持着无与伦比的魅力？不就是因为数学的血液里一直流淌着无可挑剔的逻辑严密性么？《几何原本》教你怎么从5个显而易见的公理出发，通过严密的逻辑一步步推导出400多个多定理，即便这些定理并不显而易见。

数学之美，在于形式。符号系统，对称性。牛顿力学方程、麦克斯韦的电磁学方程、薛定谔方程，这些大师们通过优雅的数学符号，简洁明晰地留下他们的思想后飘然而去，只让后人一阵惊叹。

什么是好的数学？一个数学家的品味能分辨出哪些是数学，哪些不是。

微积分形式的统一之美

微积分的“顶峰”和“终点”——三维空间的斯托克斯公式。

维度	积分区域	区域的边界	定理
1	线段	端点	微积分基本定理
2	平面	曲线	格林定理
3	曲面	曲线	斯托克斯定理
3	体	曲面	高斯定理

伽罗华群论的深刻之美

1832年5月28号，一个21岁的法国青年在和情敌的决斗中去世。他的名字叫伽罗华，他流传下来的思想叫伽罗华群论。就是靠着这个群论，他一举解决了根式求解和古希腊尺规作图领域三大难题(三等分角、化圆为方、倍立方)。根式求解是说五次及五次以上代数方程不存在求根公式。这项成就，使得伽罗华跻身人类历史有史以来最伟大的25位数学家的行列。
群论是数学中典型的通过理论创造解决实际难题的典型范例，它抓住了事物的本质，深邃，富有独创精神。可以说，伽罗华群论是数学中最美妙的华章。

几何的形体之美

几何里很多形体，自然界中是不存在的，或许我们可以通过三维打印人造出来。但是，高维空间的物体就只能靠想象了。

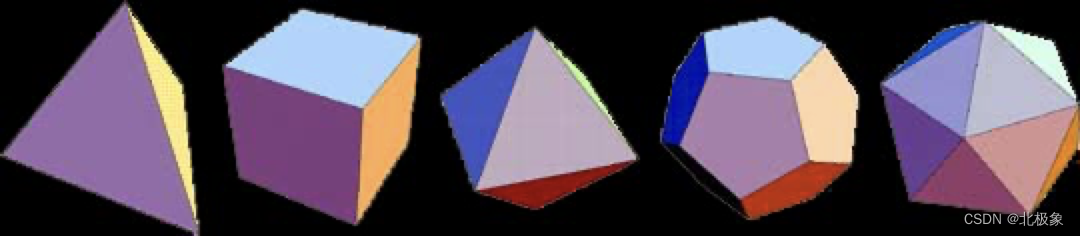
凸多面体(柏拉图多面体)仅有五种：正四面体，立方体，正八面体，正十二面体，正二十面体。估计只有正方体在自然界里天然存在，其它都是人类的构造。
宇宙那么大，我想去看看。怎么看？把它映射到一个空间来，用几何手段。

公理与定理

公理是显而易见的，大家公认的东西，定理是不显而易见，需要从公理和其它定理出发、进行证明的东西。

集合论的公理

集合论中其中一套由Skolem最后整理的公理系统，称为Zermelo-Fraenkel集合论（ZF）。实际上，这个名称通常不包括历史上远比今天具争议性的选择公理，当包括了选择公理，这套系统被称为ZFC。

• 外延公理：（Axiom of extensionality）两个集合相同，当且仅当它们拥有相同的元素。
• 分类公理：（Axiom schema of specification / axiom schema of separation / axiom schema of restricted comprehension）或称子集公理，给出任何集合及命题P(x)，存在着一个原来集合的子集包含而且只包含使P(x)成立的元素。
• 配对公理：（Axiom of pairing）假如x, y为集合，那就有另一个集合{x,y}包含x与y作为它的仅有元素。
• 并集公理：（Axiom of union）每一个集合也有一个并集。也就是说，对于每一个集合x，也总存在着另一个集合y，而y的元素也就是而且只会是x的元素的元素。
• 空集公理：存在着一个不包含任何元素的集合，我们记这个空集合为{ }。可由分类公理得出。
• 无穷公理：（Axiom of infinity）存在着一个集合x，空集{ }为其元素之一，且对于任何x中的元素y，y ∪ {y}也是x的元素。
• 替代公理：（Axiom schema of replacement）
• 幂集公理：（Axiom of power set）每一个集合也有其幂集。那就是，对于任何的x，存在着一个集合y，使y的元素是而且只会是x的子集。
• 正规公理：（Axiom of regularity / Axiom of foundation）每一个非空集合x，总包含着一元素y，使x与y为不交集。
• 选择公理：（Axiom of choice，Zermelo’s version）给出一个集合x，其元素皆为互不相交的非空集，那总存在着一个集合y（x的一个选择集合），包含x每一个元素的仅仅一个元素。

欧几里得几何公理

算术公理

意大利数学家朱塞佩·皮亚诺提出的关于自然数的五条公理系统。根据这五条公理可以建立起一阶算术系统，也称皮亚诺算术系统。

• 0是自然数；
• 每一个确定的自然数a，都有一个确定的后继数a’ ，a’ 也是自然数；
• 对于每个自然数b、c，b=c当且仅当b的后继数=c的后继数；
• 0不是任何自然数的后继数；
• 任意关于自然数的命题，如果证明：它对自然数0是真的，且假定它对自然数a为真时，可以证明对a’ 也真。那么，命题对所有自然数都真。

实数系的公理系统

设R是一个集合，若它满足下列四组公理，则称为实数系，它的元素称为实数:
(I) 域公理
(II) 序公理
(III) 连续公理
(III)(1) 阿基米德公理（也称阿基米德性质，它并不是严格意义上的公理，可以由完备性公理证明。在欧几里得的几何书中，它仅被描述为一个命题）。
阿基米德公理：对任意， 存在正整数，使。
(III)(2) 完备性公理（连续性公理）
如果与是的非空子集，满足对每个,，都有，则存在，使对任何,，都有。
称满足公理组I的集为域；满足公理组I与II的集为有序域；满足公理组I，II与(III)(1)的集为阿基米德有序域；满足公理组I～III的集为完备阿基米德有序域或完备有序域。这样，实数系就是完备阿基米德有序域。所有有理数的集合就是阿基米德有序域，但它不满足完备性公理。根据域公理，可以定义实数的减法和除法，并证明四则运算的所有性质。序公理的1与2表明关系“”是的全序。
用域公理和序公理可以定义正数、负数、不等式、绝对值，并证明它们具有通常的运算性质。加上阿基米德公理与完备性公理，可以证明实数的其他性质以及幂、方根、对数等的存在性。实数公理有多种不同的提法，常见的另一种提法是把公理组III换成
(III)’完备性公理（连续性公理）（戴德金定理）
若是的非空子集且，又对任意的及任意的恒有，则有最大元或有最小元。

关于实数的完备性，注意完备性公理中出现的“完备性”，以及关于实数完备性最常见的描述中，所谓“完备性”是对集合（有序域）性质的一种描述。
满足这些公理的任何集合，都可被认为是实数集的具体实现，或称为实数模型。 [2] 需要说明的是，实数公理下的系统是相容的，范畴的（即上述第二个意义下的完备）。

从另外一个角度来想，希尔伯特实数公理是自上而下建立数系的，用公理规定实数，然后再定义整数、正整数直至自然数。那么反过来行不行呢，实数的这些公理能不能从其他的假设中推出来呢，事实上，这就是实数的构造理论所做的事了，在菲赫金哥尔茨的《微积分学教程》的绪论中，就展示了用戴德金分割的方法从有理数定义无理数的过程，从而建立了实数，而有理数是依赖于先建立整数的，整数又是依赖于先建立自然数的，当集合论发展起来之后，自然数又依靠集合来定义了（即皮亚诺公理），集合是最原始的概念，无法再定义的概念，整个自下而上的过程可以参见兰道的《分析基础》。因此无论是从上至下还是从下至上，整个数学的基础都建立在了集合论之上，数学再也不能排除掉集合这一概念了，当英国数学家罗素发现了集合中的罗素悖论之后，引发了第三次数学危机，促使集合论又不得不加以改进，致使朴素集合论发展为近代集合论，现代的数学基础终于建立在了公理集合论的基础之上（ZFC公理系统）。

数学攀登的路径

登山有捷径，合适的学习路径能让我们更快领略到数学之美。但是，不合适的路径让我们还没看到多少风景时，就毕业了。

本人草拟的登山路径：集合论->群->矩阵和张量和变换->拓扑空间->函数论->…->数论
当然，看各人的定位，如果只是以实用为主，则线性代数，张量分析，黎曼几何和复变函数足够了。(TODO)

学习抽象的东西困难？脑子里放一个例子就行。整环不好理解，你就记住整数是它的一个典型例子。多记住几个例子，抽象也就变成具体了。

数学的符号系统

希腊字母表

序号	大写	小写	英文	汉字注音	英语音标注音
1	Α	α	alpha	阿尔法	/'ælfə/
2	Β	β	beta	贝塔	/'bi:tə/或/'beɪtə/
3	Γ	γ	gamma	格玛	/'gæmə/
4	Δ	δ	delta	德尔塔	/'deltə/
5	Ε	ε	epsilon	埃普西龙	/'epsɪlɒn/
6	Ζ	ζ	zeta	泽塔	/'zi:tə/
7	Η	η	eta	艾塔	/'i:tə/
8	Θ	θ	theta	西塔	/'θi:tə/
9	Ι	ι	iota	埃欧塔	/aɪ’əʊtə/
10	Κ	κ	kappa	堪帕	/'kæpə/
11	∧	λ	lambda	兰姆达	/'læmdə/
12	Μ	μ	mu	谬/穆	/mju:/
13	Ν	ν	nu	拗/奴	/nju:/
14	Ξ	ξ	xi	克西	/ˈzaɪ/
15	Ο	ο	omicron	欧米可戎	/əuˈmaikrən/或 /ˈɑmɪˌkrɑn/
16	∏	π	pi	派	/paɪ/
17	Ρ	ρ	rho	若	/rəʊ/
18	∑	σ	sigma	西格马	/'sɪɡmə/
19	Τ	τ	tau	套	/tɔ:/或 /taʊ/
20	Υ	υ	upsilon	宇普西龙	/ˈipsɪlon/或 /ˈʌpsɪlɒn/
21	Φ	φ	phi	弗爱	/faɪ/
22	Χ	χ	chi	凯/柯义	/kaɪ/
23	Ψ	ψ	psi	普赛	/psaɪ/
24	Ω	ω	omega	欧米嘎	/'əʊmɪɡə/或 /oʊ’meɡə/

物理与数学

物理是数学问题的源泉，给数学提供源源不断的素材；数学又是物理的工具和语言。

杨振宁1940大三时，陈省身出了一道题：如何证明每一个二维曲面保角等价于平面? 我知道如何把度量张量化成
$$A^{2}du+B^{2}d{u}^2$$
的形式，杨振宁想了很久都想不出怎样使 𝐴=𝐵。有一天，陈先生告诉他要用复变量，并写下：
$$Cdz=Adu+iBdv$$

到了 20 世纪 60 年代末期，我开始用不可积相因子的方法重新建立规范场论。有一个学期，我正在讲授广义相对论，突然注意到规范场论中的公式

Font metrics not found for font: .
与黎曼几何中的曲率公式

$$Rlijk=\partial \Gamma lij\partial xj-\partial \Gamma lij\partial xk+\Gamma mik\Gamma lmj+\Gamma mij\Gamma lmk(3)$$
不仅十分相似，而且如果把二者的符号正确地等同起来，这两个公式乃是完全一样的。当我理解到这一点时，我内心的震撼是难以形容的。
意识到规范场论与微分几何之间有密切联系。

杨振宁和吴大峻写了一篇著名的论文：《不可积相因子的概念与规范场的整体表述》[9]。在这篇论文里，他们分析了电磁场的内蕴含义，特别强调了它的整体拓扑性质。他们讨论了 Aharonov-Bohm 实验和狄拉克磁单极的量子化条件的数学意义。他们还展示了如下的一个字典 (后来被称为 “吴–杨字典”)：

推荐的数学读物

• 龚昇的《简明微积分》，《话说微积分》、《微积分五讲》、《微积分杂谈》、《线性代数五讲》，还有齐民友的《重温微积分》
• 龚昇的《简明复分析》，提纲挈领，要言不烦
• 《现代数学应用手册》五卷，华中科大2000年左右出版的，现在已经绝版了。但价值非常高，让你对整个数学大厦有直观地了解
• 《解析数论基础》，潘承洞、潘承彪兄弟写的，部分内容虽然有些过时，但仍然十分经典，我这边特意加上了书签

参考链接

• 杨振宁和当代数学