一、题目描述

输入一个奇数 n，输出一个由 * 构成的 n 阶实心菱形

输入格式：一个奇数 n。

输出格式：输出一个由 * 构成的 n 阶实心菱形。

输入样例：5

输出样例：
  *  
 *** 
*****
 *** 
  *

二、普通解法

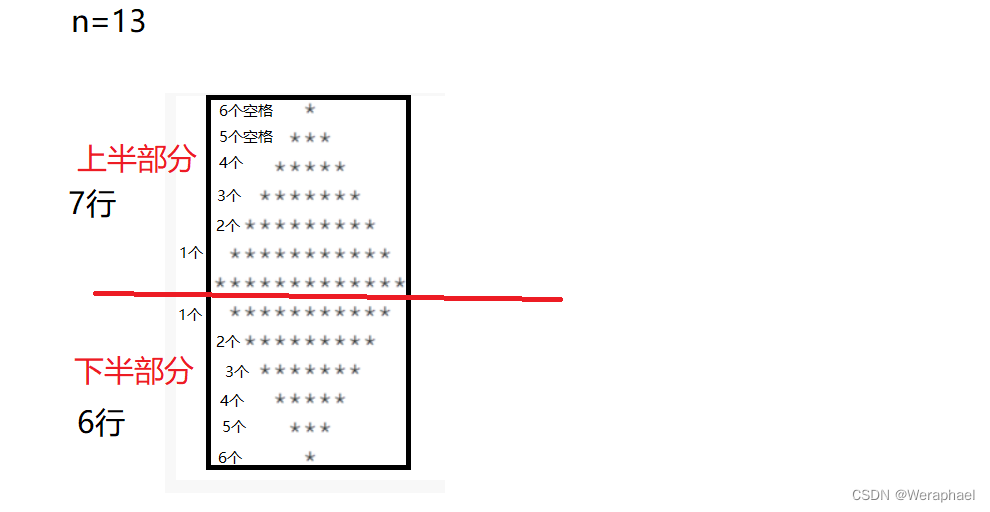
思路：若要打印第一星，首先就要先打印前6个空格，下面部分也是如此。所以，为了方便打印，我们可以分成上半部分和下半部分，上半部分空格个数由多变少，星个数由少变多；下半部分空格个数逐渐变多，星星个数逐渐变少。

因此假设n = 13，下半部分就是6行，和n的关系也就是n / 2，则上半部分就是 n - 下半部分。然后通过循环来遍历空格和星号就可以了。

对于上半部分的代码如下：

解析都在代码里了

#include <stdio.h>
int main()
{
	int n = 0;
	//输入一个奇数
	scanf("%d", &n);
	int down = n / 2; //上半部分的行数
	int up = n - down; //下半部分的行数

	//打印上半部分
	for (int i = 0; i < up; i++) //控制行
	{
		//打印空格
		//通过规律可以发现是up - 1 - i
		for (int j = 0; j < up - 1 - i; j++)
		{
			printf(" ");
		}

		//打印 *
		//因为*是奇数且递增的，所以也不难发现是2 * i + 1
		for (int j = 0; j < 2 * i + 1; j++)
		{
			printf("*");
		}
		//切记每打完一行都要换行
		printf("\n");
	}

	return 0;
}

我们可以先看看效果：

非常好！！！

接下来弄下半部分

下半部分和上半部分思路一样，关键在于找规律

#include <stdio.h>
int main()
{
	int n = 0;
	//输入一个奇数
	scanf("%d", &n);
	int down = n / 2; //上半部分的行数
	int up = n - down; //下半部分的行数

	

	//打印下半部分
	for (int i = 0; i < down; i++) //控制下半部分的行
	{
		//打印空格
		//空格的个数恰好就是下半部分的行数
		for (int j = 0; j <= i; j++)
		{
			printf(" ");
		}

		//打印 *
		//这个规律也不难发现。它是奇数且递减
		for (int j = 0; j < 2 * (down - i) - 1; j++)
		{
			printf("*");
		}
		//打印完一行别忘记换行
		printf("\n");
	}

	return 0;
}

看看下半部分结果如何

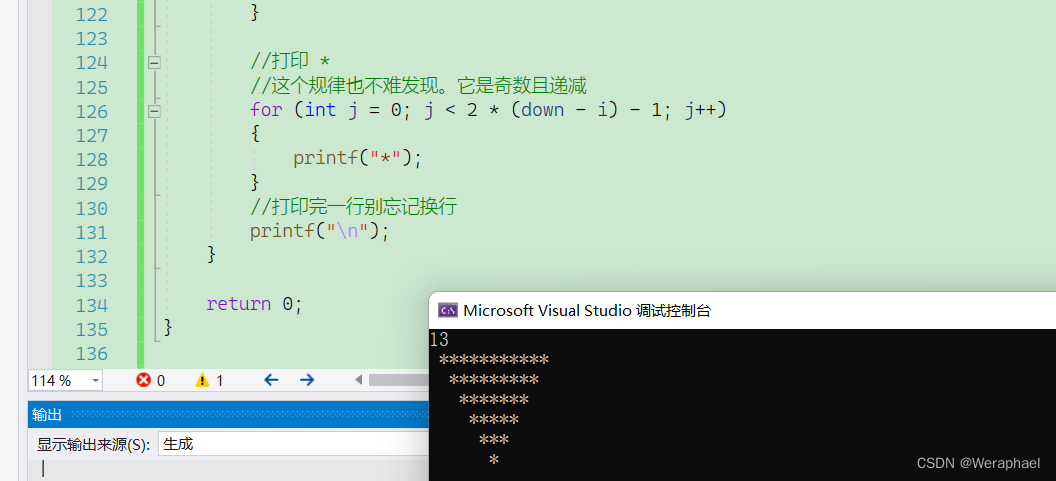
ok，也是非常的beautiful！！！

最后再把上下部分的代码结合起来

#include <stdio.h>
int main()
{
	int n = 0;
	//输入一个奇数
	scanf("%d", &n);
	int down = n / 2; //上半部分的行数
	int up = n - down; //下半部分的行数

    //打印上半部分
	for (int i = 0; i < up; i++) //控制行
	{
		//打印空格
		//通过规律可以发现是up - 1 - i
		for (int j = 0; j < up - 1 - i; j++)
		{
			printf(" ");
		}

		//打印 *
		//因为*是奇数且递增的，所以也不难发现是2 * i + 1
		for (int j = 0; j < 2 * i + 1; j++)
		{
			printf("*");
		}
		//切记每打完一行都要换行
		printf("\n");
	}

	//打印下半部分
	for (int i = 0; i < down; i++) //控制下半部分的行
	{
		//打印空格
		//空格的个数恰好就是下半部分的行数
		for (int j = 0; j <= i; j++)
		{
			printf(" ");
		}

		//打印 *
		//这个规律也不难发现。它是奇数且递减
		for (int j = 0; j < 2 * (down - i) - 1; j++)
		{
			printf("*");
		}
		//打印完一行别忘记换行
		printf("\n");
	}

	return 0;
}

程序运行结果：

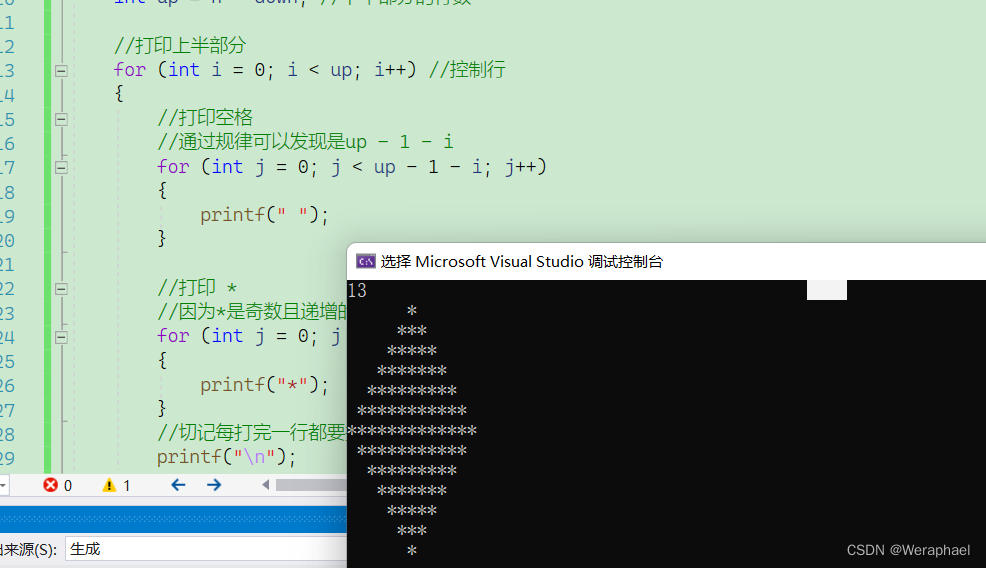
显然非常符号我们的预期！！！

三、曼哈顿距离解法

什么是曼哈顿距离呢？

一个点到中心单元的距离被称为曼哈顿距离
在二维空间中 i, j 两点的曼哈顿距离可以表示为 d(i,j)=|xi−xj|+|yi−yj|（横、纵坐标差值的绝对值之和）。

什么意思呢？接下来我举一个例子

假设我要打印一个n = 5的菱形

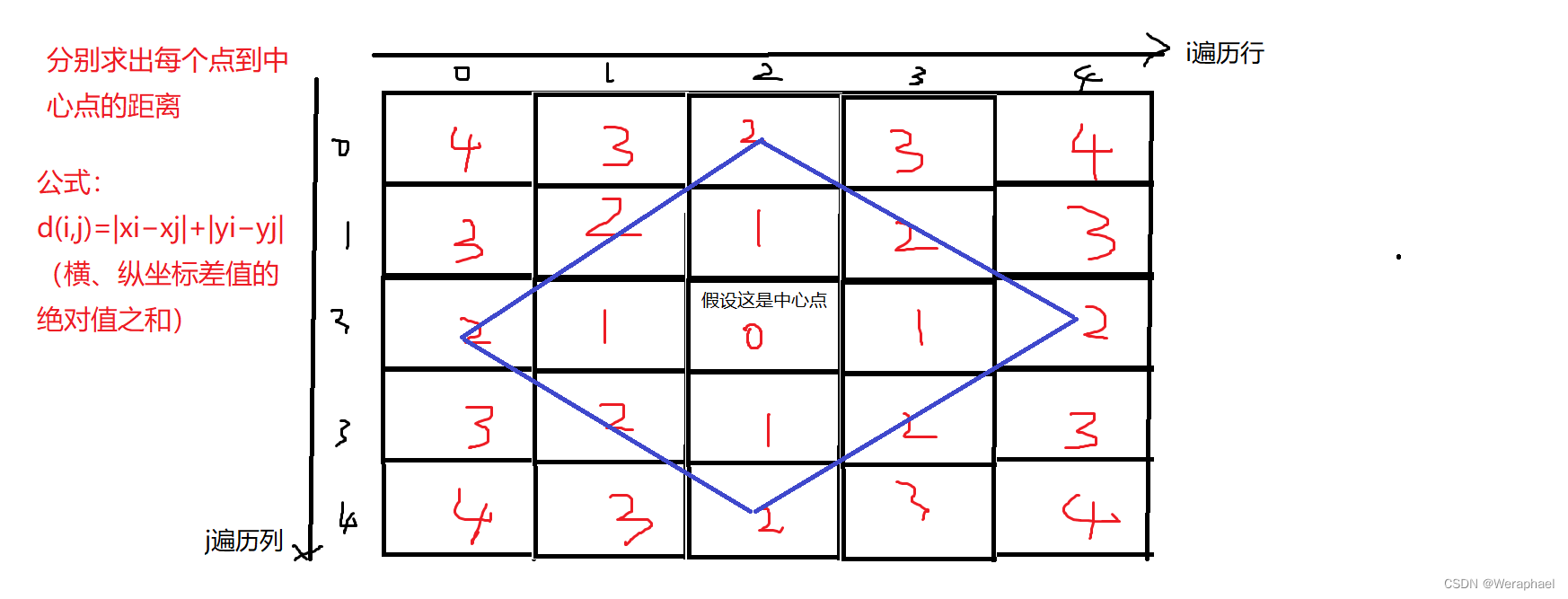
眼尖的同学已经发现，只要曼哈顿距离小于等于2的就是星星，大于2的就是空格！

接下来我们就要找n和它们的关系

中心坐标的坐标是（2,2），也就是center_x = n / 2，center_y = n / 2

同样的，只要曼哈顿距离小于等于2的就是星星，也就是只要距离是小于等于n / 2的就是星星，否则就是空格

代码实现：

#include <stdio.h>
int main()
{
	int n = 0;
	//输入一个奇数
	scanf("%d", &n);
	
	//求出中心点的坐标
	int center_x = n / 2;
	int center_y = n / 2;

	//其实就是n行n列的二维数组
	for (int i = 0; i < n; i++) //遍历行
	{
		for (int j = 0; j < n; j++) //遍历列
		{
			//abs函数返回的是两个数的绝对值
			if (abs(i - center_x) + abs(j - center_y) <= n / 2)
			{
				printf("*");
			}
			else
			{
				printf(" ");
			}
		}
		//打印完一行别忘了换行
		printf("\n");
	}
	return 0;
}

程序结果：