基础知识

二分图

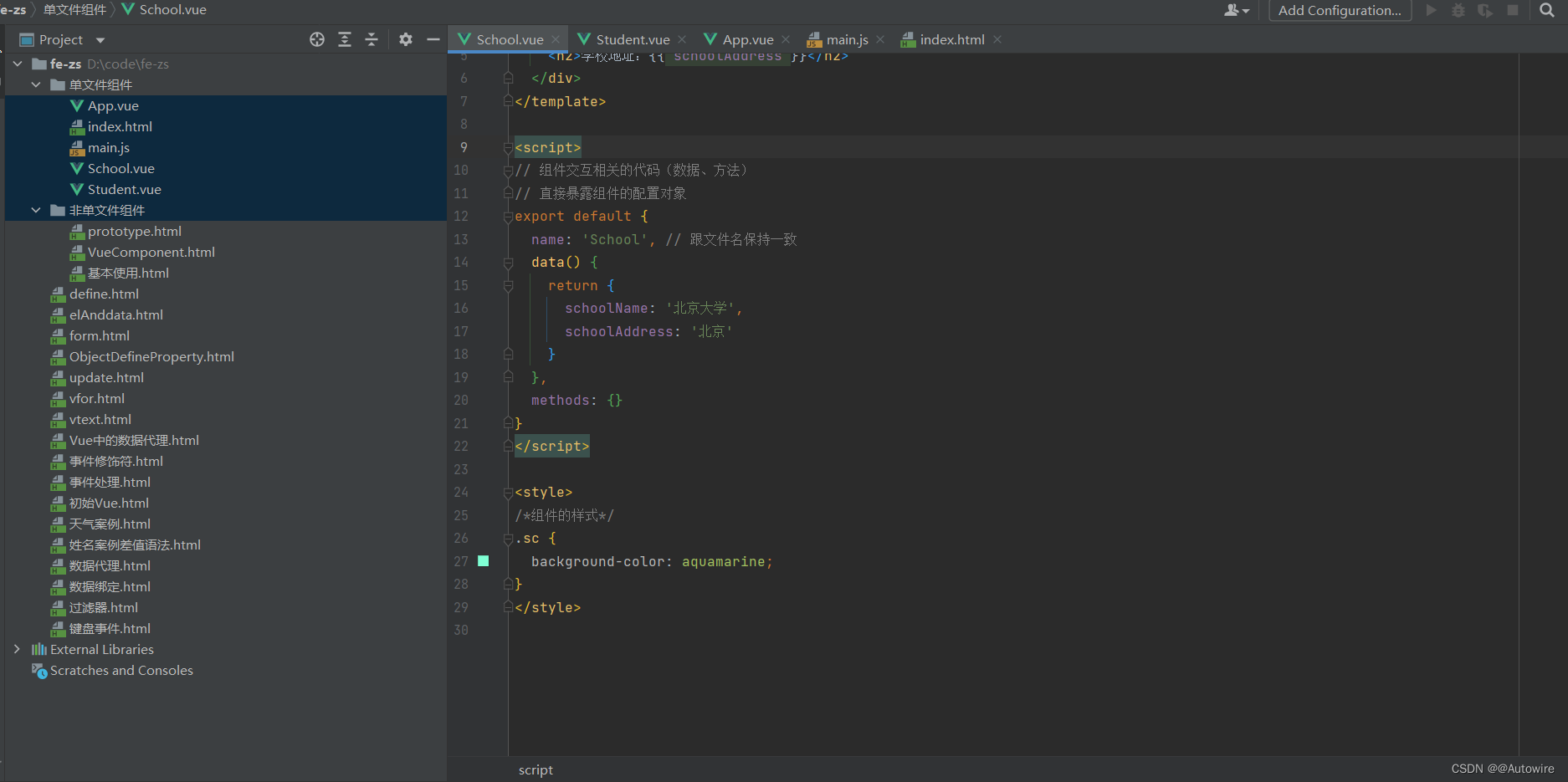
【定义】图论中的一种特殊模型。若能将无向图G=(V,E)的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为一个为二分图。

【解释】一张图要是二分图，需要满足以下几个要求：

（1） 无向图。意思就是没有方向，一旦AB俩人有连线，就说明俩人相互喜欢，配对成功，不存在A单方面喜欢B的情况。

（2） 交集为空。意思就是男的是一个集合，女的是一个集合。不存在男生集合里混入女生的情况。

（3） 任意边的两个端点分属于两个集合。意思就是，男的只能和女的配对。任何男的不能和男的配对，任何女的不能和女的配对。

满足上述条件就是二分图。

以下情况分别是非二分图和二分图。

匹配

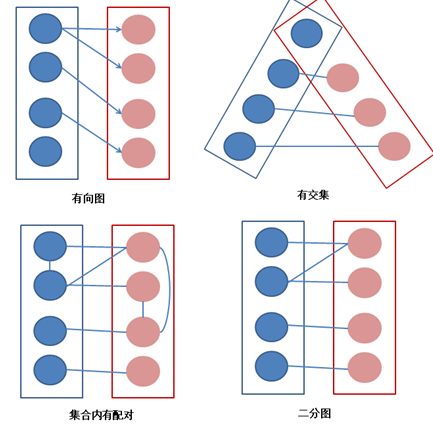
【定义】在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

【解释】结合情侣配对问题，男生女生之间互生情愫的有很多，甚至有的人对多个人都有意向，因此潜在的情侣组合方式有很多种。所谓的“任意两条边都不依附于同一个顶点”，意思就是只要我们撮合的时候，不要给某个人安排两个对象就行。作为牵线人，我们可以撮合一对，也可以撮合两对，这样每一种撮合方式，都叫一个匹配。撮合成功的这些情侣就是所谓的子图M。

最大匹配

按照上面的撮合方式，我们既不能把没有意向的两个人撮合在一起，有的人又对多个人有意向，因此可以花一点心思，尽可能地协调一下大家的意向，做到多撮合成功几对。这样，成功撮合的情侣最多的这种撮合方式，就叫最大匹配。即匹配成功数目最多的匹配方案。

最优匹配/完美匹配

解释：如果非常幸运，在我们的安排下，每个人都找到了自己心仪的对象。这种撮合方式，叫做最优匹配或完美匹配。即两边集合的所有端点都完成了匹配。

交替路和增广路

交替路和增广路是用来解决新配对的时候发生冲突的问题。这里要结合具体问题解释才能更清楚。那么我们来结合具体问题，看看这个交替路和增广路有啥用处。

考虑一个下面这个二分图，怎么找到最大的匹配呢？

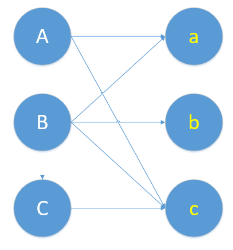
一个自然的思路是，一个一个的配对。首先给A配对。一看A和a有意向，那就先把他俩撮合到一起。

现在效果就变成这样了。

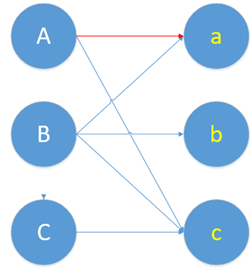
蓝色的是他们本身有意向的情况，就是原始二分图，要记得蓝线连一块并不叫“匹配边”，而是“非匹配边”。红色的是我们给他们配对了，红线才叫“匹配边”。

好了，A的问题暂时性解决了，轮到B了。结果b也想和a配对。

这时候，谁才能和a在一起呢？交替路和增广路就是解决这个冲突的。

这时候，我们要找一条交替路，就是依次经过非匹配边（蓝线）、匹配边（红线）。那么我们从B出发，开始找交替路了。我们找到了

（非匹配边） (匹配边) (非匹配边)

B--------------a----------------A-----------------c

B和c都是没有被匹配过的点，而它又是这条交替路的起点和终点。这条交替路就是增广路。增广路是交替路的特例

现在我们要做一个取反操作，怎么取呢，就是将上面这条增广路的匹配边变成不匹配边，不匹配边变成匹配边。

（匹配边） (非匹配边) (匹配边)

B--------------a----------------A-----------------c

还是用红色表示匹配边，蓝色表示非匹配边。画在图上，现在的匹配变成这样。

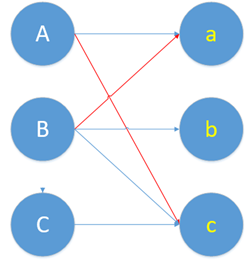
然后，我们发现，刚刚的冲突问题解决了。由B和a在一起，A和c在一块。

回过头来，再想一下增广路是怎么解决冲突问题的。增广路的核心特点就是“起点终点都是非匹配点”，这样就导致非匹配边比匹配边多了一条。增广路建立连接时，必须建立在两者有意向的基础上。这样我们取反，也就是交换匹配和非匹配边的身份。我们就多得到了一条匹配边。这个取反的过程，就是把原本匹配上的两个人拆散，给第三个人腾位置。就是那篇很火的博客里所说的，核心思想就是“腾位置”。

最后，我们把上图的配对问题彻底解决完。

AB的问题都解决了，轮到C了。C要和c配对，又发生冲突了。于是，又要使用增广路来增加一个匹配了。

（非）（匹）（非）（匹）（非）

C--------c-----------A----------a----------B---------b

取个反得到：

（匹）（非）（匹）（非）（匹）

C--------c-----------A----------a----------B---------b

画成图长这样

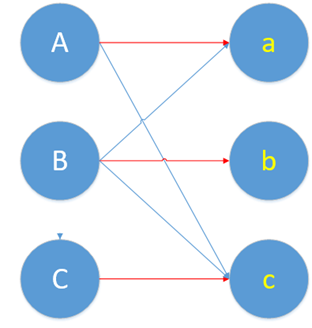
现在，ABC的配对都解决了。我们找到了最大匹配。由于A\B\C\a\b\c都找到了自己的心仪对象。因此，这个最大匹配也是完美匹配。

下面这个链接里的二分图，就没能找到完美匹配。

匈牙利算法（二分图） - 神犇(shenben) - 博客园www.cnblogs.com

深度优先和广度优先

上述是深度优先匈牙利算法。就是冲突了立刻用增广路来解决。

另外一种是广度优先匈牙利算法。思路是，冲突了就换一个心仪对象，看另一个心仪对象是不是也配对了，要是都配对了，再用增广路来解决。

广度优先的流程是这样的：

（1）A和a连上。

（2）B也想连a，但是a被连了，就找下一个心仪对象b。

（3）b没有被连上，B和b就连在一起。

（4）轮到C的时候，C找心仪对象c。

（5）c也没被连上，所以C和c连一起。

匈牙利算法

上述利用增广路找最大匹配的算法，就叫做匈牙利算法。

总结一下匈牙利算法：

每个点从另一个集合里挑对象，没冲突的话就先安排上，要是冲突了就用增广路径重新匹配。重复上述思路，直到所有的点都找到对象，或者找不到对象也找不到增广路。

下面为详细的流程介绍：

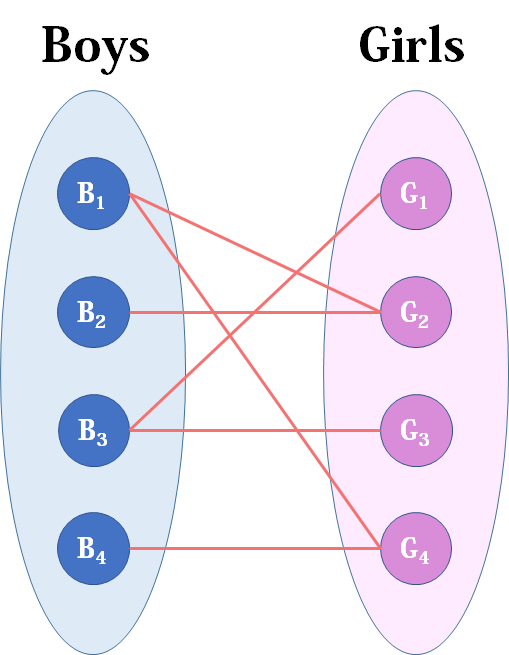
现在Boys和Girls分别是两个点集，里面的点分别是男生和女生，边表示他们之间存在“暧昧关系"。最大匹配问题相当于，假如你是红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？（数学表述：在二分图中最多能找到多少条没有公共端点的边）

现在我们来看看匈牙利算法是怎么运作的：

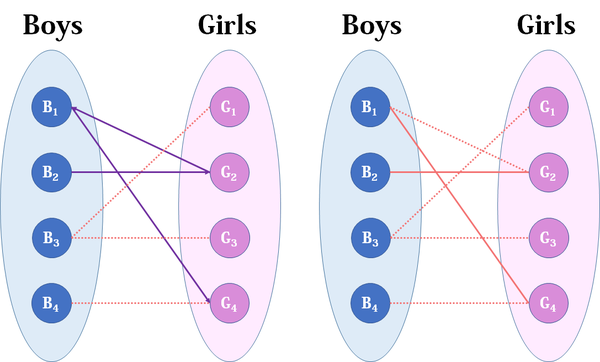
我们从B1看起（男女平等，从女生这边看起也是可以的），他与G2有暧昧，那我们就先暂时把他与G2连接（注意这时只是你作为一个红娘在纸上构想，你没有真正行动，此时的安排都是暂时的）。

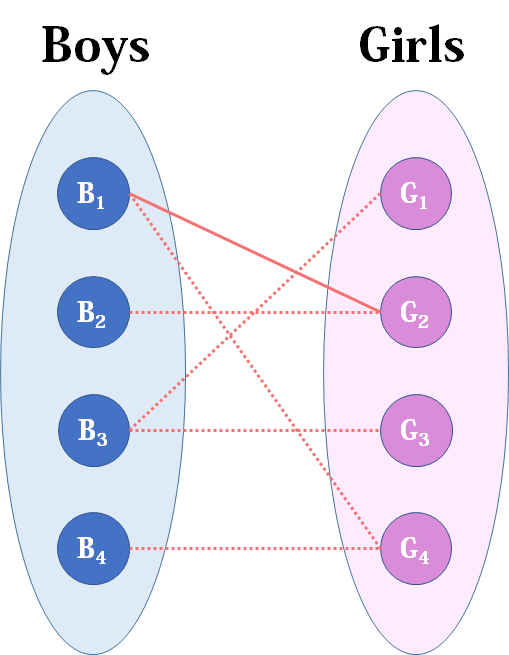
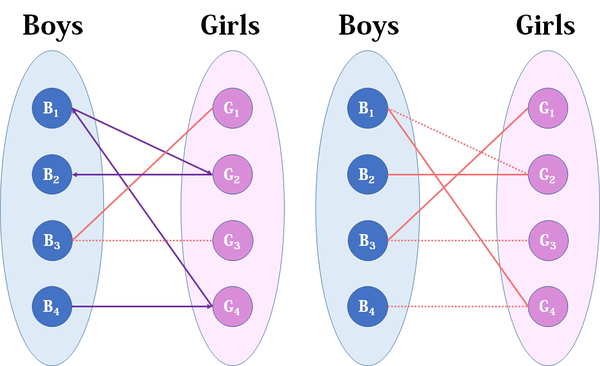
来看B2，B2也喜欢G2，这时G2已经“名花有主”了（虽然只是我们设想的），那怎么办呢？我们倒回去看G2目前被安排的男友，是B1，B1有没有别的选项呢？有，G4，G4还没有被安排，那我们就给B1安排上G4。

然后B3，B3直接配上G1就好了，这没什么问题。至于B4，他只钟情于G4，G4目前配的是B1。B1除了G4还可以选G2，但是呢，如果B1选了G2，G2的原配B2就没得选了。我们绕了一大圈，发现B4只能注定单身了，可怜。（其实从来没被考虑过的G3更可怜）

这就是匈牙利算法的流程，至于具体实现，我们来看看代码：

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}

其实流程跟我们上面描述的是一致的。注意这里使用了一个递归的技巧，我们不断往下递归，尝试寻找合适的匹配。

KM算法（Kuhn-Munkres Algorithm）

KM算法解决的是带权二分图的最优匹配问题。

还是用上面的图来举例子，这次给每条连接关系加入了权重，也就是我们算法中其他模块给出的置信度分值。

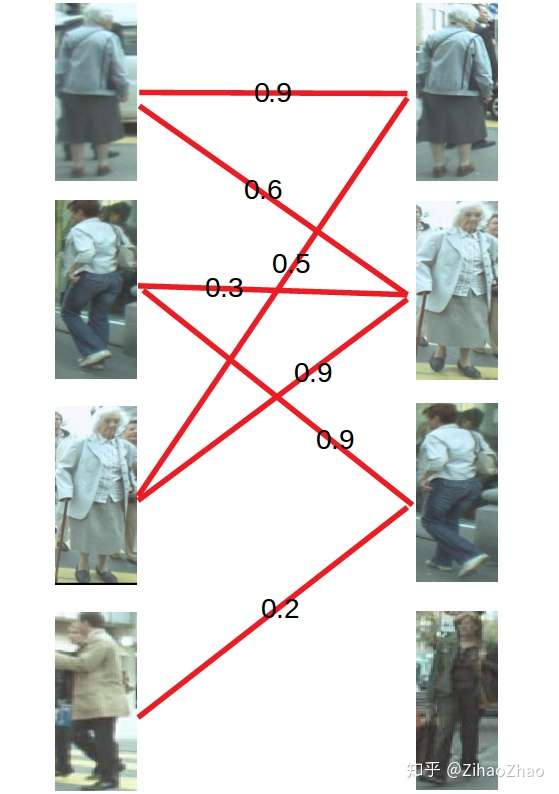
KM算法解决问题的步骤是这样的。

第一步

首先对每个顶点赋值，称为顶标，将左边的顶点赋值为与其相连的边的最大权重，右边的顶点赋值为0。

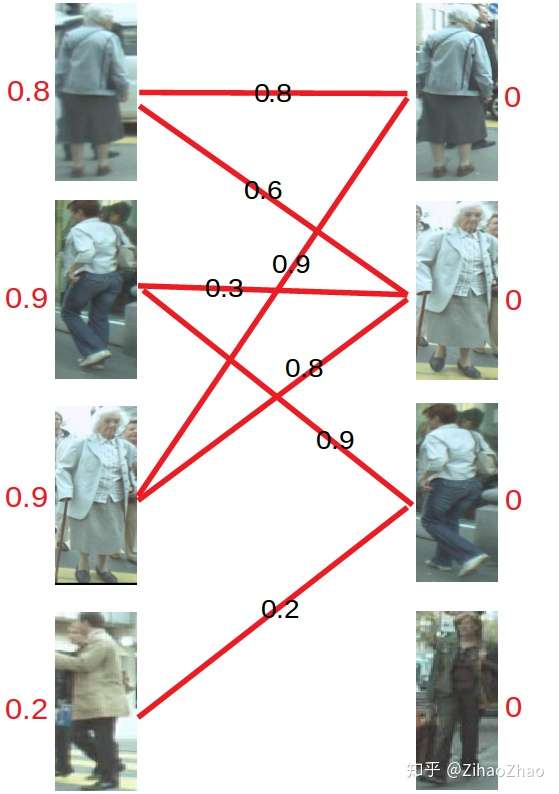
第二步，开始匹配

匹配的原则是只和权重与左边分数（顶标）相同的边进行匹配，若找不到边匹配，对此条路径的所有左边顶点的顶标减d，所有右边顶点的顶标加d。参数d我们在这里取值为0.1。

对于左1，与顶标分值相同的边先标蓝。

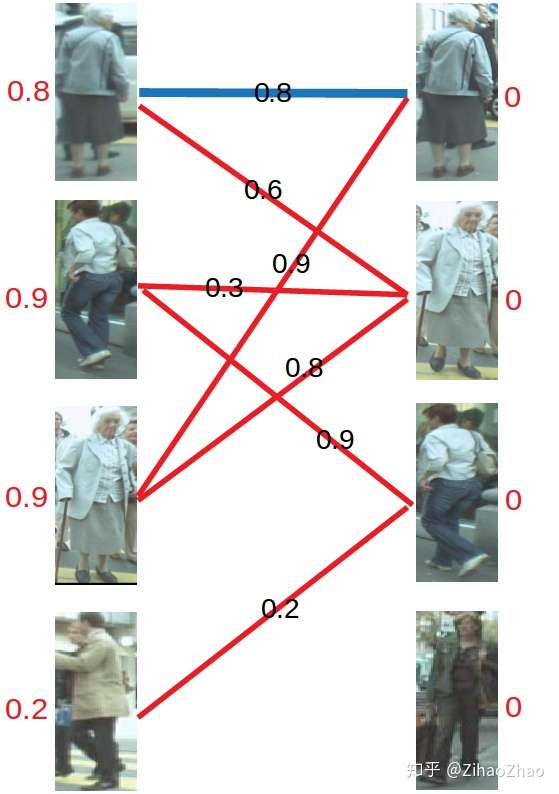
然后是左2，与顶标分值相同的边标蓝。

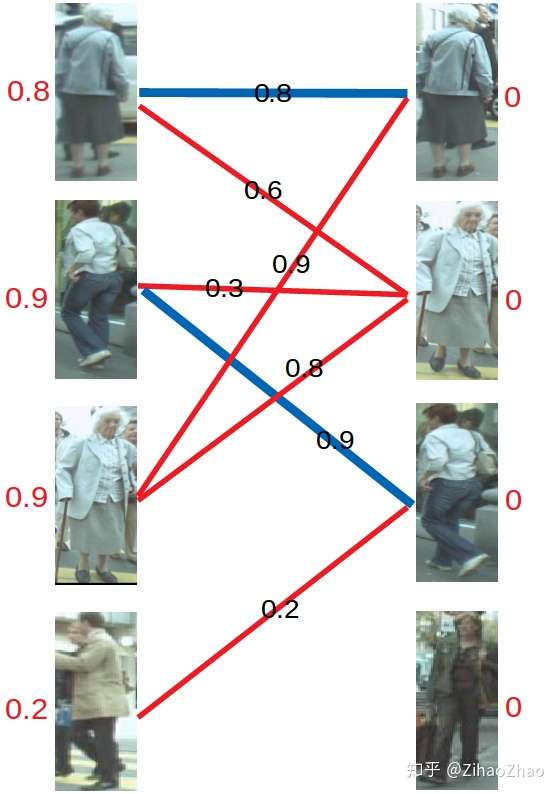
然后是左3，发现与右1已经与左1配对。首先想到让左3更换匹配对象，然而根据匹配原则，只有权值大于等于0.9+0=0.9（左顶标加右顶标）的边能满足要求。于是左3无法换边。那左1能不能换边呢？对于左1来说，只有权值大于等于0.8+0=0.8的边能满足要求，无法换边。此时根据KM算法，应对所有冲突的边的顶点做加减操作，令左边顶点值减0.1，右边顶点值加0.1。结果如下图所示。

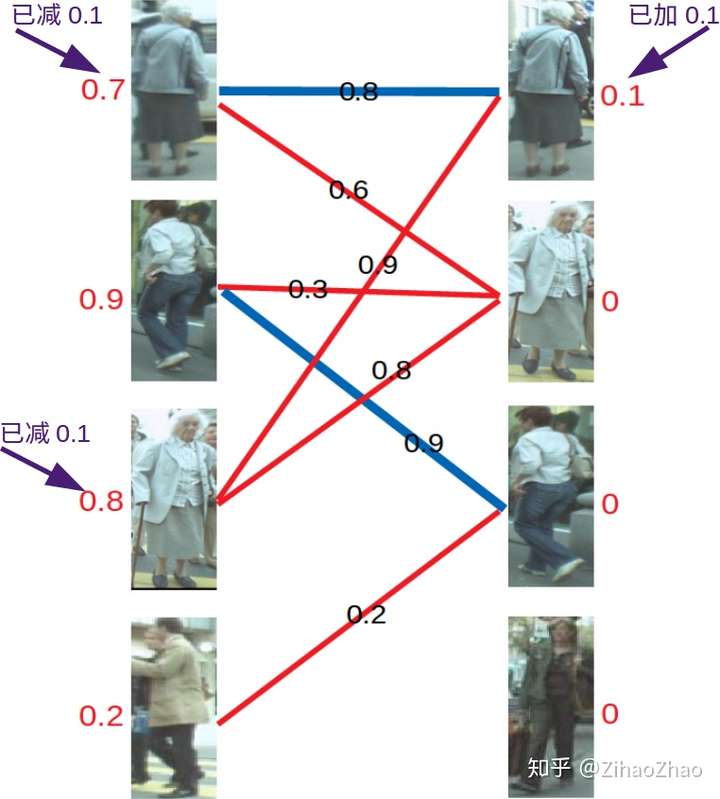
再进行匹配操作，发现左3多了一条可匹配的边，因为此时左3对右2的匹配要求只需权重大于等于0.8+0即可，所以左3与右2匹配！

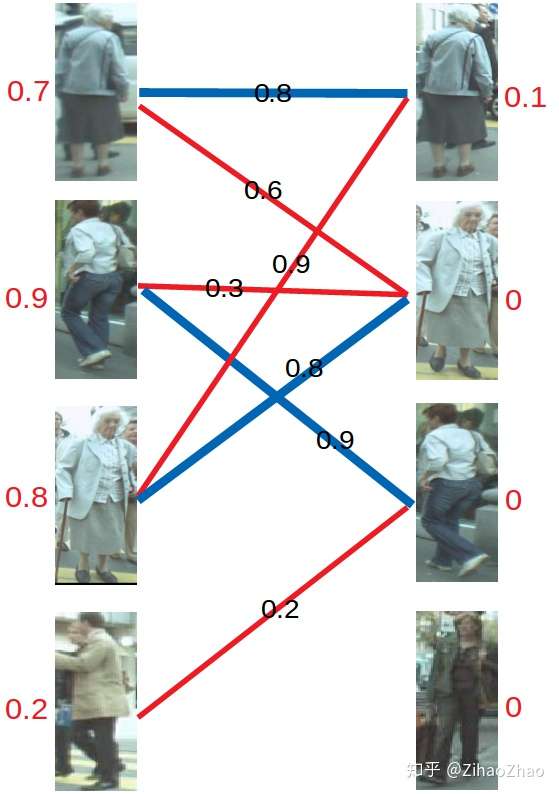
最后进行左4的匹配，由于左4唯一的匹配对象右3已被左2匹配，发生冲突。进行一轮加减d操作，再匹配，左四还是匹配失败。两轮以后左4期望值降为0，放弃匹配左4。

至此KM算法流程结束，三对目标成功匹配，甚至在左三目标预测不够准确的情况下也进行了正确匹配。可见在引入了权重之后，匹配成功率大大提高。

最后还有一点值得注意，匈牙利算法得到的最大匹配并不是唯一的，预设匹配边、或者匹配顺序不同等，都可能会导致有多种最大匹配情况，所以有一种替代KM算法的想法是，我们只需要用匈牙利算法找到所有的最大匹配，比较每个最大匹配的权重，再选出最大权重的最优匹配即可得到更贴近真实情况的匹配结果。但这种方法时间复杂度较高，会随着目标数越来越多，消耗的时间大大增加，实际使用中并不推荐。