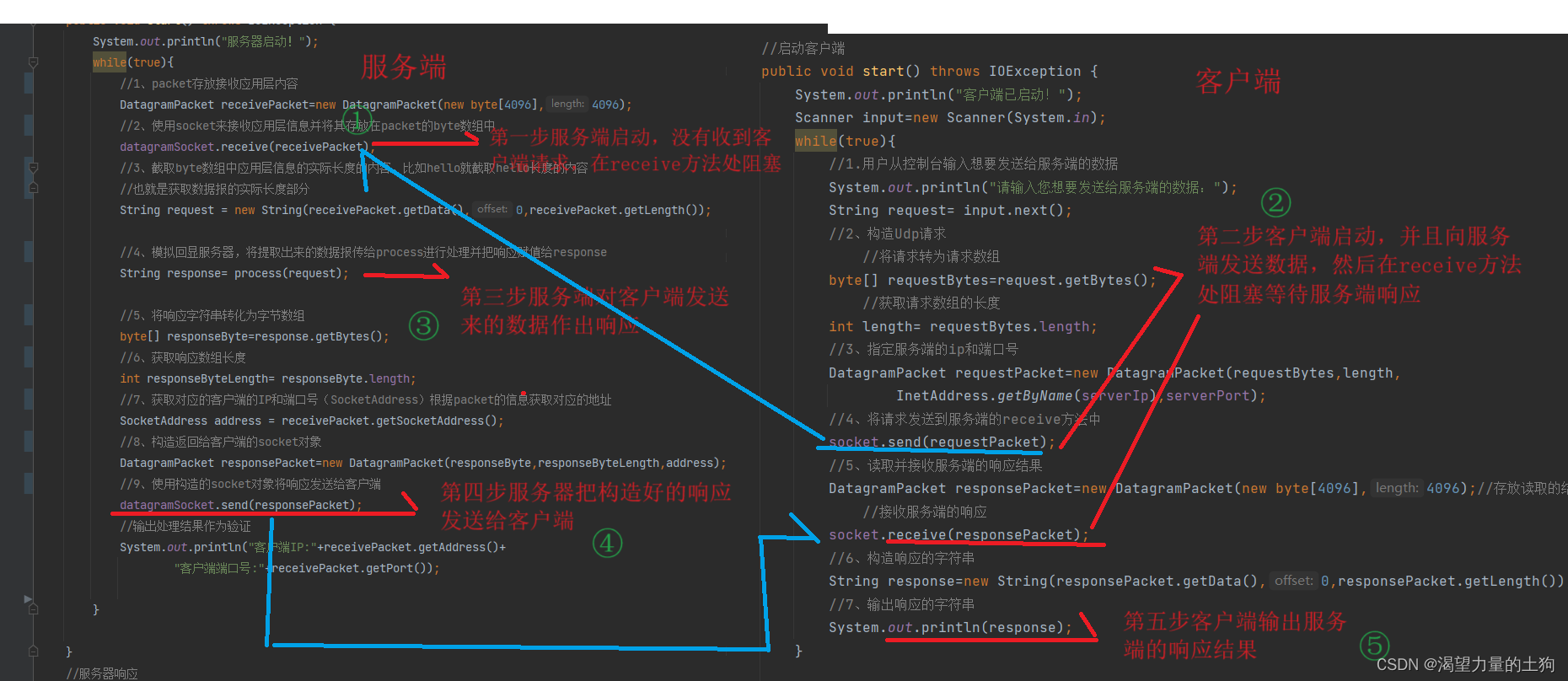
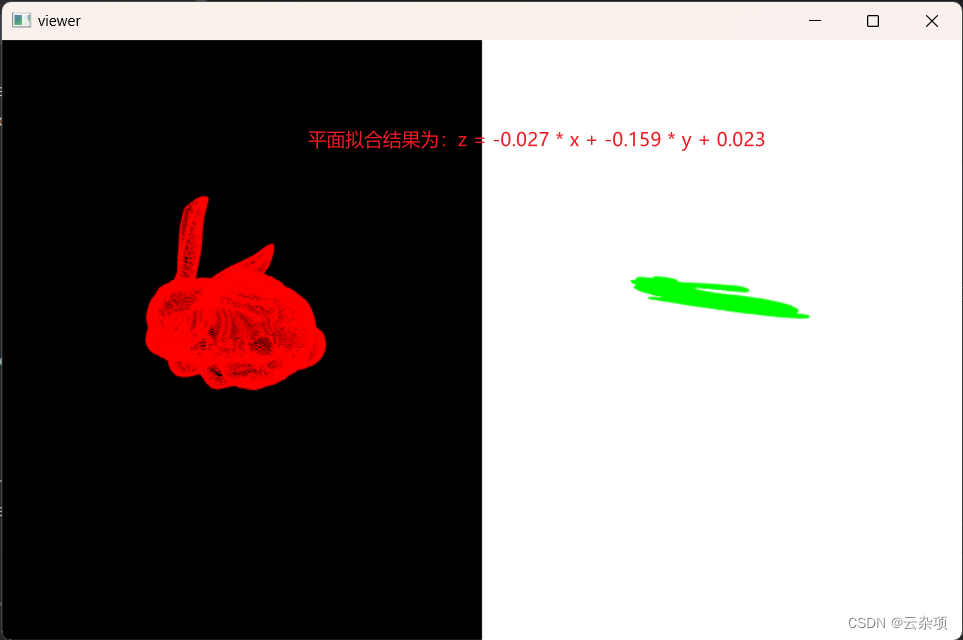
1、内容简介
略
46-可以交流、咨询、答疑
2、内容说明
略
4 取标段的分析
取标装置是贴标机的核心部件之一,是影响贴标质量和贴标精度的重要因素,取标段是通过取标板与标签的相切运动使得涂有胶水的取标板从标签盒中粘取标签纸[4],理论上取标过程中取标板与标签应即无相对滑动又无法向相对位移,但研究表明上述两个条件无法同时满足[5]。当取标板与标签有相对滑动时会导致粘在取标板上的标签出现褶皱、不平整以及搓标签;当取标板与标签有法向相对位置时,取标板与标签不能保持相切,这都能导致取标失败。为保证有效取标,通常以取标板与标签无相对滑动为设计条件,然后通过安装弹簧式标签盒消除取标板与标签法向相对位移的影响,从而保证整个取标过程中取标板与标签保持良好接触[6]。
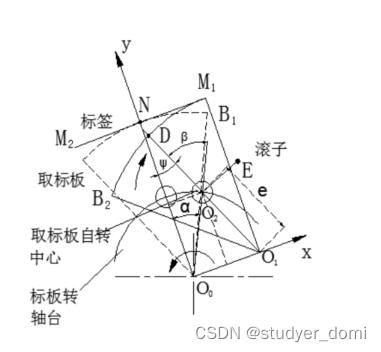

取标段滚子运动分析如图5所示。标板转轴台绕O0匀速转动,取标板自转中心为O2,曲率中心为O1,曲率半径为Rb。取标板在绕O2自转的同时绕O0公转,公转半径为R0。取标板的偏心距为e,D为取标板上弧线中点,标签M1M2的长度为L,中点为N。转盘转角α为O0O2与y轴的夹角,取标板的摆角β为O0O2与O1O2的夹角,取标板的自转角Ψ为O1O2与y轴的夹角。点E为滚子中心,固定在与取标板自转中心相连接的连杆上,滚子放在槽形凸轮中。

图5 取标段的分析
当标板转轴台逆时针方向转动时,取标板顺时针方向摆动。当B1与M1接触时开始取标,当B2与M2接触时完成取标,取标板走过的弧长与标签长度相等。取标板在取标签时的摆动关于y轴对称[7]。当D与N接触时α=β=Ψ=0,切点D的坐标为(0,Rb)。
当转盘转角为α时,D与N相切。取标板摆过的弧长等于它粘取到的标签的长度[8],即SB1D=M1N,则:

(1)
同时,β=

+α,其中

≤L/2Rb (2)
联立(1)和(2)可得:

(3)
对于给定的α通过式(3)就可以计算出相应的取标板摆角β。
当开始取标时,取标板的初始自转角为

,代入式(1)得:

(4)
则取标板初始摆角为:

(5)
在△O0O2E中,根据余玄定理得:

(6)

(7)
由图5可知:

; (8)
而

;

为固定值,

,

为固定值;
所以

在△O0O2E中,

(9)
联立式(3)(9),通过对方程组求解,可以得到E点的运动轨迹即为取标工位滚子的理论运动轨迹,也就是凸轮的理论运动轨迹。
3、仿真分析
略
clc;close all;clear
%% ---------------基本参数----------------
r0=124; % 取标板公转半径
r=130; % 凸轮基圆半径
R=11; % 滚柱半径
o2e=54; % 传动力臂
o0o2=r0;
rb=240.6; % 取标板曲率半径
e=124; % 取标板偏心距
o1o2e=83.89; % 传动夹角
l=170; % 标签长度
alpha0=asin(l/2/r0-e/r0*sin(l/2/rb))*180/pi;
alpha0=19.8;
fai0=l/2/rb;% 弧度
alpha=alpha0:1:alpha0+67; % 转盘转角
%% ------------计算取标板摆角---------
syms beta xx y
for i=1:length(alpha)
f1=solve(y*rb*pi/180==r0*sin(alpha(i)*pi/180)+e*sin(y/180*pi),y); % y角度
xx(i)=f1+alpha(i);
end
for i=1:length(alpha)
x(i)=double(xx(1,i)); % x角度
end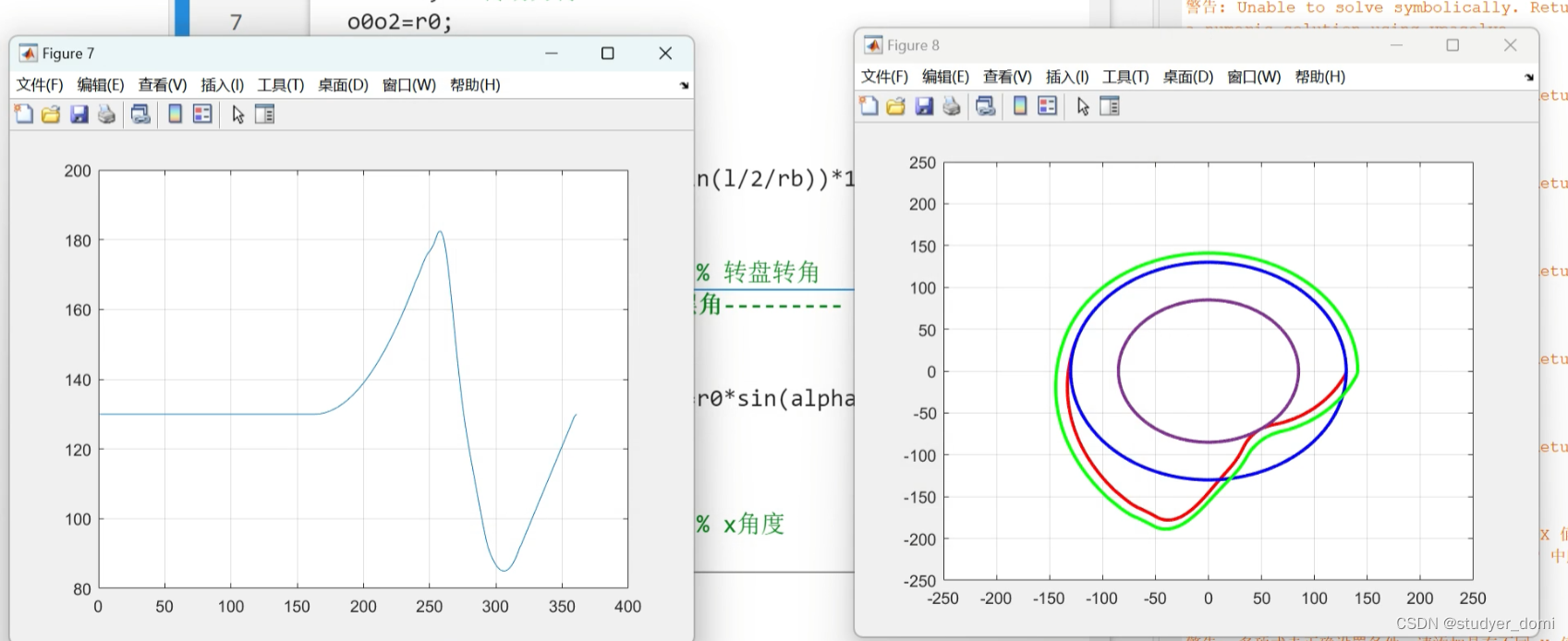
4、参考论文
略