一、算法原理

平面方程的一般表达式为：
$$Ax+By+Cz+D=0(C\ne 0)$$
即：
$$Z=-\frac{A}{C}x-\frac{B}{C}y-\frac{D}{C}$$
记：
$$a_0=-\frac{A}{C},a_1=-\frac{B}{C},a_2=-\frac{D}{C}$$
所以：
$$Z=a_{0}x+a_{1}y+a_2$$
要用该 n 个点拟合平面方程，即使：
$$\sum _{n=1}^N(a_{0}x+a_{1}y+a_2{)}^2->min$$
要使S最小，对a,b,c求偏导

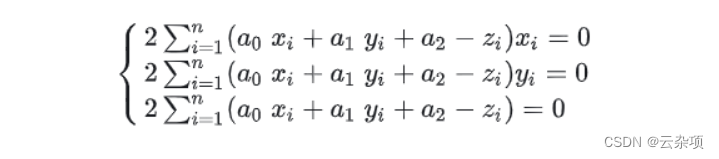
改写成矩阵的形式为：

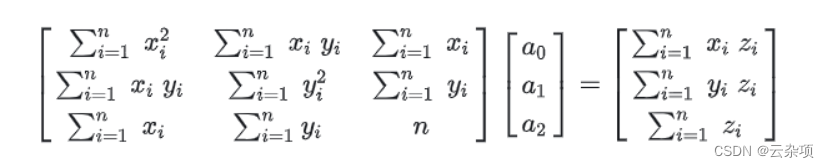
二、代码

from pclpy import pcl
import numpy as np


def CloudShow(cloud1, cloud2):
    """
    Args:在一个窗口可视化多个点云
        cloud1: 点云数据1
        cloud2: 点云数据2
    """
    viewer = pcl.visualization.PCLVisualizer("viewer")  # 建立可刷窗口对象 窗口名 viewer
    v0 = 1  # 设置标签名（0, 1标记第一个窗口）
    viewer.createViewPort(0.0, 0.0, 0.5, 1.0, v0)  # 创建一个可视化的窗口
    viewer.setBackgroundColor(0.0, 0.0, 0.0, v0)  # 设置窗口背景为黑色
    single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud1, 255.0, 0, 0.0)  # 将点云设置为红色
    viewer.addPointCloud(cloud1,  # 要添加到窗口的点云数据。
                         single_color,  # 指定点云的颜色
                         "sample cloud1",  # 添加的点云命名
                         v0)  # 点云添加到的视图

    v1 = 2  # 设置标签名（2代表第二个窗口）
    viewer.createViewPort(0.5, 0.0, 1.0, 1.0, v1)  # 创建一个可视化的窗口
    viewer.setBackgroundColor(255.0, 255.0, 255.0, v1)  # 设置窗口背景为白色
    single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud2, 0.0, 255.0, 0.0)  # 将点云设置为绿色
    viewer.addPointCloud(cloud2,  # 要添加到窗口的点云数据。
                         single_color,  # 指定点云的颜色
                         "sample cloud2",  # 添加的点云命名
                         v1)  # 点云添加到的视图

    # 设置点云窗口（可移除对点云可视化没有影响）
    viewer.setPointCloudRenderingProperties(0,  # 设置点云点的大小
                                            1,  # 点云像素
                                            "sample cloud1",  # 识别特定点云
                                            v0)  # 在那个窗口可视化
    viewer.setPointCloudRenderingProperties(0,  # 设置点云点的大小
                                            1,  # 点云像素
                                            "sample cloud2",  # 识别特定点云
                                            v1)  # 在那个窗口可视化
    # viewer.addCoordinateSystem(1.0)  # 设置坐标轴 坐标轴的长度为1.0
    # 窗口建立
    while not viewer.wasStopped():
        viewer.spinOnce(10)


def plane(cloud, normal_vector):
    coeffs = pcl.ModelCoefficients()  # 创建了一个模型系数对象
    coeffs.values.append(normal_vector[0])  # a = 0.0
    coeffs.values.append(normal_vector[1])  # b = 0.0
    coeffs.values.append(normal_vector[2])  # c = 1.0
    coeffs.values.append(normal_vector[3])  # d = 0.0

    # 创建滤波器
    proj = pcl.filters.ProjectInliers.PointXYZ()  # 过滤器对象 proj，用于将点云投影到一个模型上。
    proj.setModelType(0)  # 模型类型被设为 0，代表使用平面模型。
    proj.setInputCloud(cloud)  # 将cloud点云数据进行处理
    proj.setModelCoefficients(coeffs)  # 处理参数coeffs
    cloud_projected = pcl.PointCloud.PointXYZ()  # 建立保存点云
    proj.filter(cloud_projected)  # 将投影结果保存

    return cloud_projected

if __name__ == '__main__':
    cloud1 = pcl.PointCloud.PointXYZ()
    reader = pcl.io.PCDReader()  # 设置读取对象
    reader.read('res/bunny.pcd', cloud1)  # 读取点云保存在cloud中

    # 调用函数，生成离散点
    x, y, z = cloud1.x, cloud1.y, cloud1.z
    N =  cloud1.size()
    # ------------------------构建系数矩阵-----------------------------
    A = np.array([[sum(x ** 2), sum(x * y), sum(x)],
                  [sum(x * y), sum(y ** 2), sum(y)],
                  [sum(x), sum(y), N]])

    B = np.array([[sum(x * z), sum(y * z), sum(z)]])

    # 求解
    X = np.linalg.solve(A, B.T)
    print('平面拟合结果为：z = %.3f * x + %.3f * y + %.3f' % (X[0], X[1], X[2]))
    a, b, c, d = X[0], X[1], -1, X[2]
    plane_cloud = plane(cloud1, [a, b, c, d])  # 获得投影后的点云数据

    # ------------------ 可视化点云 -----------------
    CloudShow(cloud1, plane_cloud) 

三、结果

1.左边原点云、右边最小二乘法拟合平面后点云投影

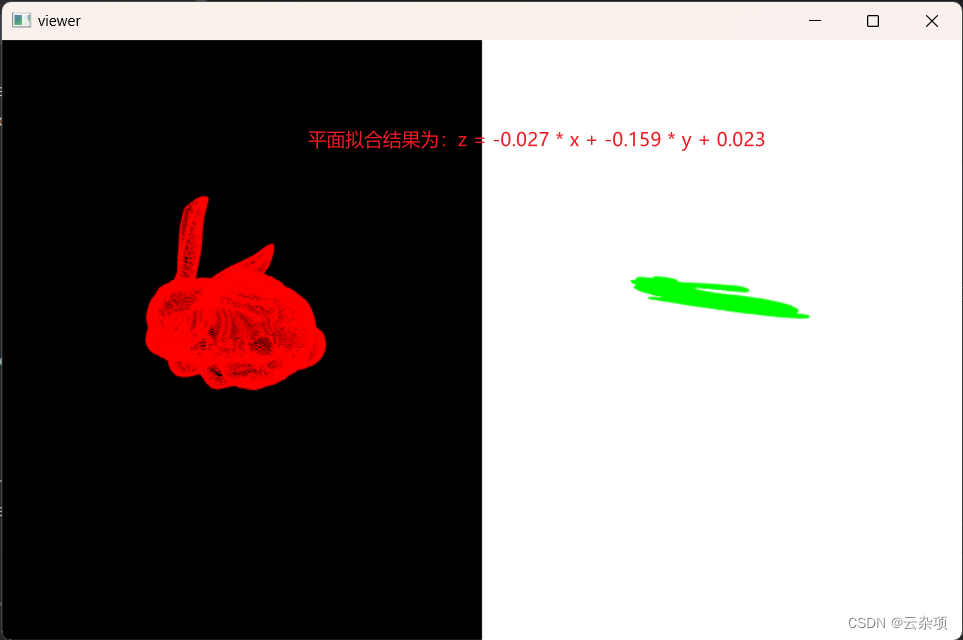
四、相关数据

最小二乘法拟合参考链接：最小二乘拟合平面(python/C++版) - 知乎 (zhihu.com)