一、5种多目标优化算法简介
多目标优化算法是用于解决具有多个目标函数的优化问题的一类算法。其求解流程通常包括以下几个步骤:
1. 定义问题:首先需要明确问题的目标函数和约束条件。多目标优化问题通常涉及多个目标函数,这些目标函数可能存在冲突,需要在不同目标之间进行权衡。
2. 生成初始解集:通过随机生成或者其他混沌映射生成一组初始解集。这些初始解集通常是在可行解空间内随机分布的。
3. 评估解集:对初始解集中的每个解进行评估,计算其在各个目标函数上的值。这些值可以用来衡量解的优劣程度。
4. 更新解集:根据一定的策略,从当前解集中选择一部分解作为父代,通过种群更新策略生成新的解作为子代。然后将父代和子代合并形成新的解集。
5. 重复迭代:重复执行步骤3和步骤4,直到满足停止准则。停止准则可以是达到一定的迭代次数、达到一定的收敛程度或者其他条件。
6. 输出结果:最终得到的解集即为多目标优化问题的近似最优解集。这些解集通常构成了问题的帕累托前沿,表示了在不同目标之间的权衡关系。
1.1多目标萤火虫算法MOFA

1.2非支配排序鲸鱼优化算法NSWOA

1.3多目标水母搜索算法MOJS

1.4多目标人工蜂鸟算法MOAHA

1.5多目标粒子群优化算法MOPSO

二、5种多目标优化算法性能对比
为了测试5种算法的性能将其求解9个多目标测试函数(zdt1、zdt2 、zdt3、 zdt4、 zdt6 、Schaffer、 Kursawe 、Viennet2、 Viennet3),其中Viennet2 与Viennet3的目标数为3,其余测试函数的目标数为2,并采用6种评价指标(IGD、GD、HV、Coverage、Spread、Spacing)进行评价对比
2.1部分代码
close all;
clear ;
clc;
addpath('./MOJS/')%添加算法路径
addpath('./MOFA/')%添加算法路径
addpath('./NSWOA/')%添加算法路径
addpath('./MOPSO/')%添加算法路径
addpath('./MOAHA/')%添加算法路径
%%
% TestProblem测试问题说明:
%一共9个多目标测试函数1-9分别是: zdt1 zdt2 zdt3 zdt4 zdt6 Schaffer Kursawe Viennet2 Viennet3
%%
TestProblem=3;%测试函数1-9
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100; % Population size 种群大小
params.Nr = 100; % Repository size 外部存档
params.maxgen=50; % Maximum number of generations 最大迭代次数
numOfObj=MultiObj.numOfObj;%目标函数个数
%% 算法求解,分别得到paretoPOS和paretoPOF
[Xbest1,Fbest1] = NSWOA(params,MultiObj);
[Xbest2,Fbest2] = MOJS(params,MultiObj);
[Xbest3,Fbest3] = MOAHA(params,MultiObj);
[Xbest4,Fbest4] = MOPSO(params,MultiObj);
[Xbest5,Fbest5] = MOFA(params,MultiObj);
FbestData(1).data=Fbest1;
FbestData(2).data=Fbest2;
FbestData(3).data=Fbest3;
FbestData(4).data=Fbest4;
FbestData(5).data=Fbest5;
%% 获取测试函数的真实pareto前沿
True_Pareto=MultiObj.truePF;
%% 计算每个算法的评价指标
% ResultData的值分别是IGD、GD、HV、Coverage、Spread、Spacing
for i=1:5
Fbest=FbestData(i).data;
ResultData(i,:)=[IGD(Fbest,True_Pareto),GD(Fbest,True_Pareto),HV(Fbest,True_Pareto),Coverage(Fbest,True_Pareto),Spread(Fbest,True_Pareto),Spacing(Fbest,True_Pareto)];
end
%% 画图
PlotFigure;
2.2部分结果
(1)以zdt3为例:


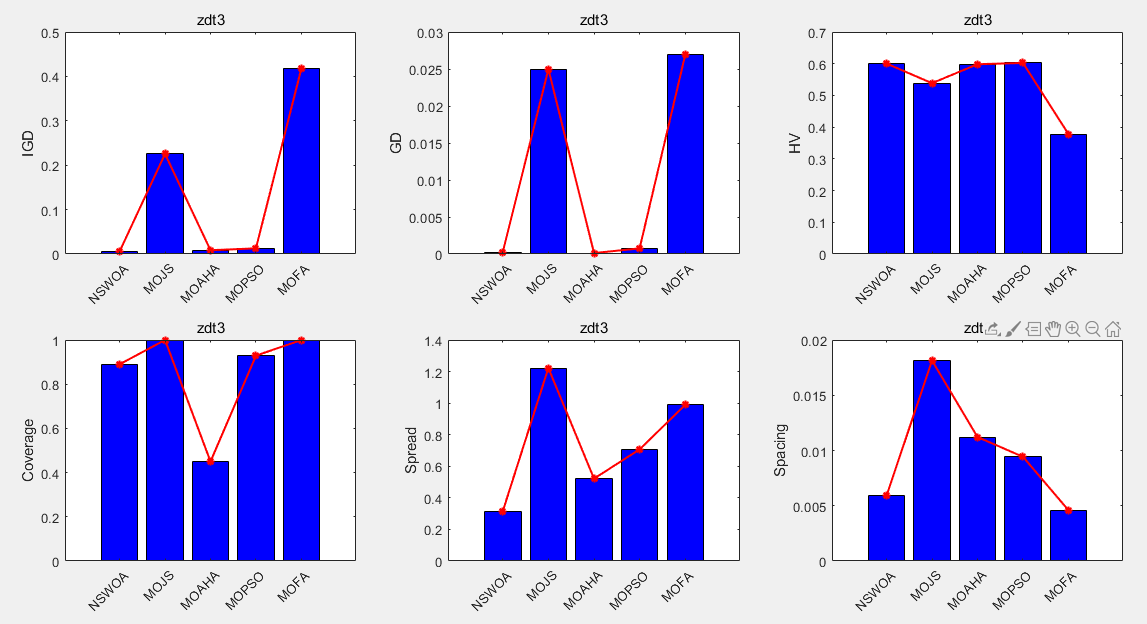
(2)以Viennet2为例: