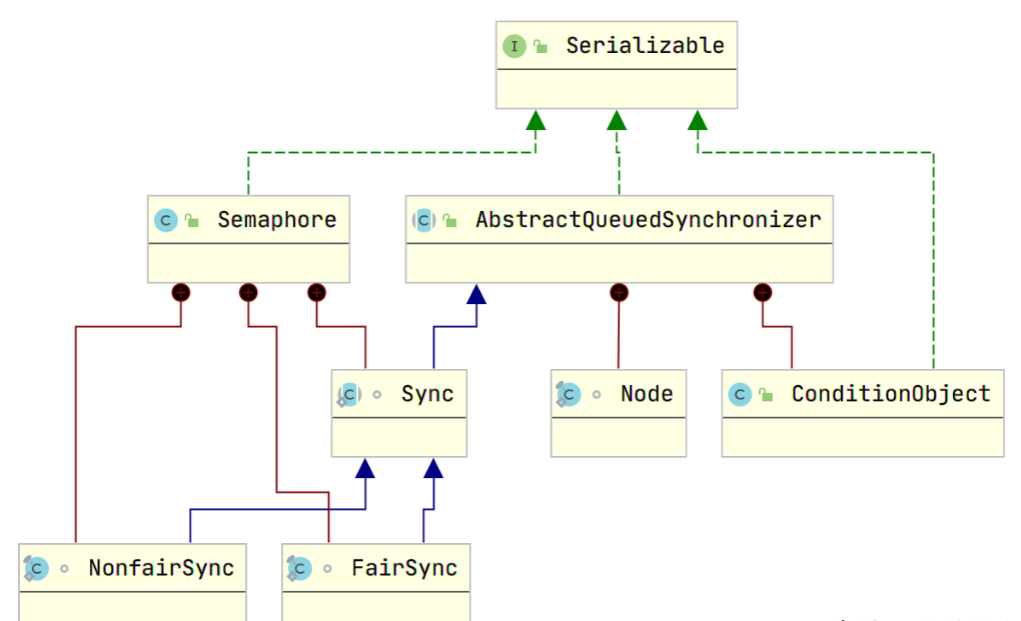
回文子串

这道题主要难在dp数组的定义以及递推关系的构建。如果直接用 dp[i] 表示[0,i]子串中包含的回文串的数目，是无法找到递推关系的。通过回文串的性质可以构造这样的递推关系：对于判断[i,j]是否是回文串，如果s[i] == s[j]，只需要考察[i+1,j-1]是否回文串；如果s[i] != s[j]，一定不是回文串。因此构建 dp[i][j] 表示下标范围是[i,j]的子串是否是回文串。
由于初始没有进行匹配，都初始化为false即可。
对于遍历顺序，[i+1,j-1]推导[i,j]。所以i应该从大到小，j从小到大。

class Solution {
public:
	int countSubstrings(string s) {
		vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
		int result = 0;
		for(int i = s.size() - 1; i >= 0; i--) {
			for(int j = i; j < s.size(); j++) {  // 直接从i开始即可，j是终止下标
				if(s[i] == s[j]) {
					if(j - i <= 1) {
						// 如果子串只有一个或两个字符，没法用递推公式推
						dp[i][j] = true;
						result++;
					}
					else if(dp[i + 1][j - 1]) {
						dp[i][j] = true;
						result++;
					}
				}
			}
		}
		return result;
	}
};

双指针法

分为一个中心元素和两个中心元素两种情况。用每个元素作为中心累加回文串的数目。

class Solution {
public:
	int countSubstrings(string s) {
		int result = 0;
		for(int i = 0; i < s.size(); i++) {
			result += extend(s, i, i, s.size());
			result += extend(s, i, i+1, s.size());
		}
		return result;
	}
	int extend(const string& s, int i, int j, int n) {
		int res = 0;
		while(i >= 0 && j < n && s[i] == s[j]) {
			i--;
			j++;
			res++;
		}
		return res;
	}
};

最长回文子序列

这道题可以直接定义 dp[i][j] 为下标 [i,j] 部分子串的最长回文子序列长度。
递推公式：如果s[i] == s[j]，则 dp[i][j] = dp[i + 1][j - 1] + 2。如果不相等，则[i,j]部分子串的结果取决于[i+1,j]和[i, j-1]两个子串结果的最大值，也就是取考虑s[i]和考虑s[j]的最大值。
初始化与遍历顺序这两点和上一道题是一样的。

class Solution {
public:
	int longestPalindromeSubseq(string s) {
		vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
		for(int i = s.size() - 1; i >= 0; i--) {
			for(int j = i; j < s.size(); j++) {
				if(s[i] == s[j]) {
					if(j - i <= 1) {
						dp[i][j] = j - i + 1;
					}
					else {
						dp[i][j] = dp[i + 1][j - 1] + 2;
					}
				}
				else {
					dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
				}
			}
		}
		return dp[0][s.size() - 1];
	}
};