2.2 时间复杂度

• 什么是时间复杂度？

  评估算法时间开销

  $$T(n)=O(f(n))$$

  在实际求解中，只留表达式中最高阶的部分，丢弃其他部分。

• 如何求解？

  • 求解步骤

    1.找到一个最深层的基本操作；

    2.分析该操作执行次数x与问题规模n的关系**$x=f(n)$**；

    3.x的数量级$O(x)$就是时间复杂度$T(n)$；

  • 求解原则

    1.顺序执行的代码只会影响常数项，可忽略。

    2.只需挑一个基本操作分析它的执行次数与n的关系即可。

    3.如果有多层嵌套循环，只需关注最深层循环了几次。

• 规则

  • 1.加法规则

    $T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))$

  • 2.乘法规则

    $T(n)=T_1(n)\ast T_2(n)=O(f(n))\ast O(g(n))=O(f(n)\ast g(n))$

• 常见渐近时间复杂度

  $O(1)<O(lo{g}_{2}n)<O(n)<O(nlo{g}_{2}n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$

• 时间复杂度分类

  最坏时间复杂度、平均时间复杂度、最好时间复杂度

  只考虑最坏时间复杂度。

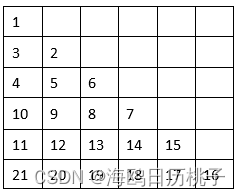
• 循环时间复杂度总结