核实后将予以处理。 感谢您为社区和谐做出的贡献。
一般来说,大多数台式电脑的功率在250W左右,也就是每4小时耗一度电。 一般有每小时100W左右的低功耗计算机,也有每小时1000W左右的高功耗计算机。 对于笔记本电脑来说,每小时约为 35W 至 120W。 即每24小时至9小时发电1度电。
这取决于计算机配置。 配置越高,功率越大。 你可以自己下载鲁大师。 里面有功耗预估,不过这是最大功耗。 待机,我不知道你的意思是电脑已打开但未运行程序,还是电脑处于睡眠状态。 状态下,一般电脑睡眠状态的功耗基本为0
通常,一般笔记本的功率在65W左右。 (电源适配器(即充电器)的额定输出电压为19V,额定输出电流为3.42A,因此额定功率为64.98W。)现在按额定功率65W、1000W来计算。 小时/65W=约15小时,即1度电约15小时用完。 一小时用电量约为0.07千瓦时,也就是说一天为1.68千瓦时。 当然,这是理论值。 这取决于您的电源的实际功率。 例如,如果你玩游戏、听音乐、在线看电影、聊天,将笔记本电脑的亮度调到最亮,你的实际功率绝对不仅仅是65W。
台式电脑的功耗是多少瓦? ●这取决于台式计算机的配置。 配置的高低与功耗有关。 而且,台式机的功耗也有比较大的动态范围,根据启用多少运行内存,功耗也会有所不同。 见下图。 上班后,我把电脑主机和显示器一起打开,没有打开任何正在运行的软件。 我用钳形表测量了它的电流值,为0.398A。 计算功率为220V×0.398A=87.56w。 简单来说,台式电脑的功耗一般都不是很大。 主机内的配件,如CPU、主板、硬盘、光驱、显卡等,功耗为150W。 如果液晶显示器是17英寸,则消耗40W。 每小时总耗电量为190W。 190×1=190瓦时,也就是0.19千瓦时的电,也就是说这台电脑使用4-5小时大约用1千瓦时的电。 这是最大功耗。 事实上,并非所有硬件都能以最大功率工作。 ,楼主可以按照80%左右来计算。 以上是个人实际使用测得的功率。 仅供提问者参考。知足常乐上海2019.12.11
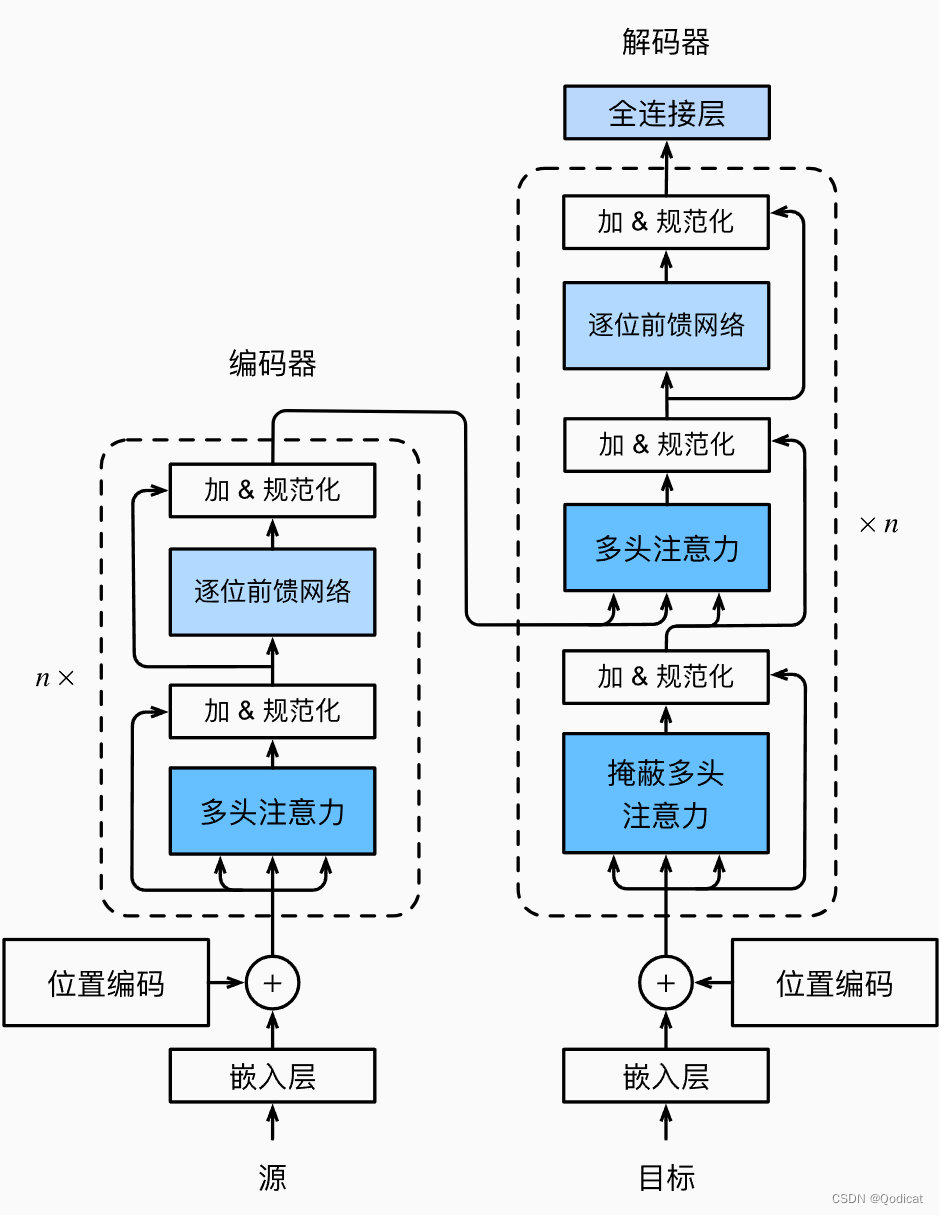

![[嵌入式系统-33]:RT-Thread -18- 新手指南:三种不同的版本、三阶段学习路径](https://img-blog.csdnimg.cn/direct/8f13e2ae00a346afaf1720ea4c921455.png)
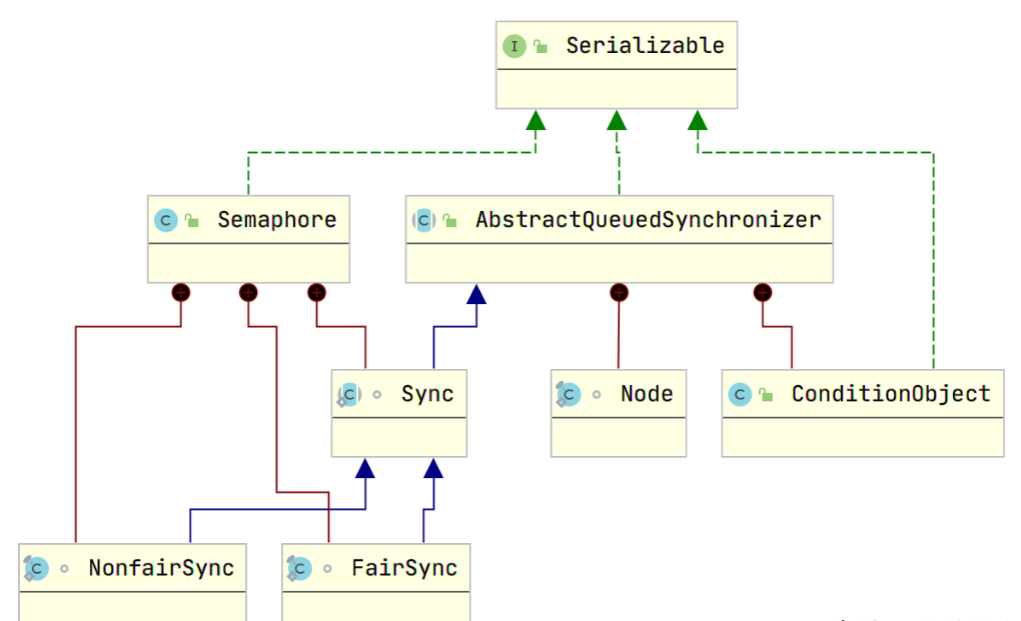


![Python算法题集_实现 Trie [前缀树]](https://img-blog.csdnimg.cn/direct/5a897d6e99aa4f639286febc56714d68.png#pic_left)