参考:《百面机器学习》
PR曲线
TP( True Positive):真正例
FP( False Positive):假正例
FN(False Negative):假反例
TN(True Negative):真反例
精确率(Precision): P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
召回率(Recall): R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
精确率(Y),也称为查准率,衡量的是分类正确的正样本个数占分类器判定为正样本的样本个数的比例。
召回率(X),也称为查全率,衡量的是分类正确的正样本个数占真正的正样本个数的比例。
F1-score
F1 score是分类问题中常用的评价指标,定义为精确率(Precision)和召回率(Recall)的调和平均数。
F
1
=
2
1
P
r
e
c
i
s
i
o
n
+
1
R
e
c
a
l
l
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
F1=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}=\frac{2×Precision×Recall}{Precision+Recall}
F1=Precision1+Recall12=Precision+Recall2×Precision×Recall
F1 score 综合考虑了精确率和召回率,其结果更偏向于 Precision 和 Recall 中较小的那个。可以更好地反映模型的性能好坏,而不是像算术平均值直接平均模糊化了 Precision 和 Recall 各自对模型的影响。
补充另外两种评价方法:
加权调和平均:
上面的 F1 score 中, Precision 和 Recall 是同等重要的,而有的时候可能希望我们的模型更关注其中的某一个指标,这时可以使用加权调和平均:
F
β
=
(
1
+
β
2
)
1
1
P
r
e
c
i
s
i
o
n
+
β
2
×
1
R
e
c
a
l
l
=
(
1
+
β
2
)
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
β
2
×
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
F_{\beta}=(1+\beta^{2})\frac{1}{\frac{1}{Precision}+\beta^{2}×\frac{1}{Recall}}=(1+\beta^{2})\frac{Precision×Recall}{\beta^{2}×Precision+Recall}
Fβ=(1+β2)Precision1+β2×Recall11=(1+β2)β2×Precision+RecallPrecision×Recall
当
β
>
1
\beta > 1
β>1 时召回率有更大影响,
β
<
1
\beta < 1
β<1 时精确率有更大影响,
β
=
1
\beta = 1
β=1 时退化为 F1 score。
即F2,召回率权重更高,F0.5,精确率权重更高。
(根据式子可以看出
β
\beta
β越大,P就可以小一些,也就是不重要)
几何平均数:
G
=
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
G=\sqrt{Precision×Recall}
G=Precision×Recall
ROC曲线
真阳性率(True Positive Rate): T P R = T P P = T P T P + F N TPR =\frac{TP}{P}=\frac{TP}{TP+FN} TPR=PTP=TP+FNTP
假阳性率(False Positive Rate,FPR): F P R = F P N = F P F P + T N FPR =\frac{FP}{N}=\frac{FP}{FP+TN} FPR=NFP=FP+TNFP
真阳性率(Y),也称为灵敏度,衡量的是分类正确的正样本个数占真正的正样本个数的比例。
假阳性率(X),也称为特异度,衡量的是错误识别为正例的负样本个数占真正的负样本个数的比例。
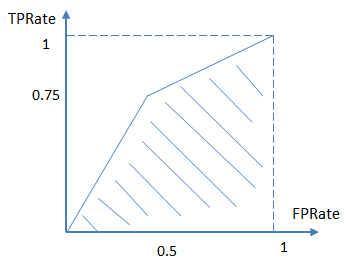
AUC
参考链接:AUC的计算方法及相关总结
A
U
C
=
∑
i
∈
positiveclass
rank
i
−
M
(
1
+
M
)
2
M
×
N
A U C=\frac{\sum_{i \in \text { positiveclass }} \operatorname{rank}_{i}-\frac{M(1+M)}{2}}{M \times N}
AUC=M×N∑i∈ positiveclass ranki−2M(1+M)
AUC指的是ROC曲线下的面积大小,该值能够反映基于ROC曲线衡量出的模型性能。AUC越大,说明分类器越可能把真正的正样本排在前面,分类性能越好。
参考链接
如何理解机器学习和统计中的AUC?
PR和ROC对比
-
当正负样本的分布发生变化时,ROC曲线的形状能够基本保持不变,而P-R曲线的形状一般会发生较剧烈的变化。
ROC曲线能够尽量降低不同测试集带来的干扰,在正负样本不平衡时,更能反映模型本身的特性。
-
如果研究者希望更多地看到模型在特定数据集上的表现,P-R曲线则能够更直观地反映其性能。