机器学习笔记之前馈神经网络——非线性问题
- 引言
- 回顾:关于非线性问题
- 解决非线性问题的三种方式
引言
上一节介绍了从机器学习到深度学习的过渡,并介绍了深度学习的发展过程。本节将主要介绍如何使用神经网络处理非线性问题
回顾:关于非线性问题
关于非线性问题,我们并不陌生,例如在核方法思想与核函数介绍中提到的最简单的非线性问题——亦或分类问题:
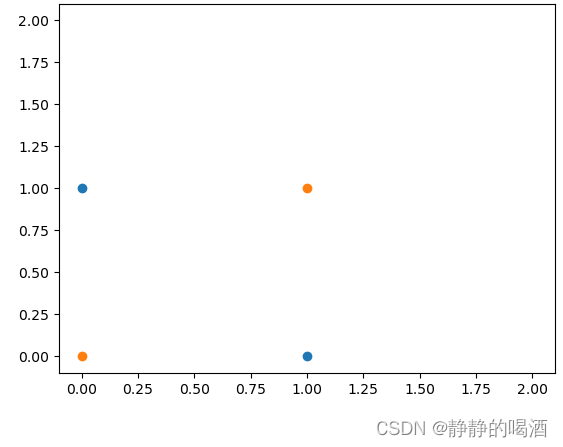
针对二维特征无法将亦或问题线性可分的情况,通过添加一维新特征的方法,使其在三维特征空间中实现分类:
x
(
i
)
=
[
x
1
(
i
)
,
x
2
(
i
)
,
(
x
1
(
i
)
,
−
x
2
(
i
)
)
]
i
=
1
,
2
,
3
,
4
x^{(i)} = \left[x_1^{(i)},x_2^{(i)}, \left(x_1^{(i)}, - x_2^{(i)}\right)\right] \quad i=1,2,3,4
x(i)=[x1(i),x2(i),(x1(i),−x2(i))]i=1,2,3,4
对应的分类效果表示如下:
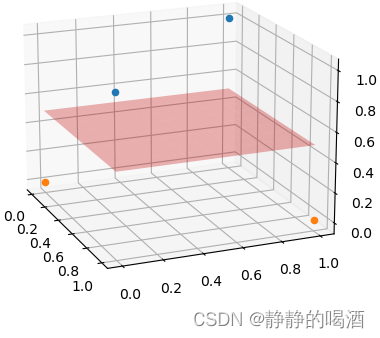
虽然这个例子比较简单,但可以观测到关于非线性分类问题的处理思想——通过高维特征转换将非线性问题转化为高维线性问题。这也是核方法的主要思想。
当然,非线性问题不仅存在于分类任务中,回归任务中同样也存在非线性问题。例如介绍过的高斯过程回归,从权重空间角度观察,其核心思想就是将贝叶斯线性回归与核技巧相结合:
- 将样本特征空间 X \mathcal X X经过高维特征转化得到 ϕ ( X ) \phi(\mathcal X) ϕ(X),从而引发模型参数 W \mathcal W W的高维转换;
- 再使用贝叶斯线性回归的两步走推断:
- 求解高维转换后
W
\mathcal W
W的后验概率分布
P
(
W
∣
D
a
t
a
)
\mathcal P(\mathcal W \mid Data)
P(W∣Data):
P ( W ∣ D a t a ) ∼ N ( μ W , Σ W ) { μ W = 1 σ 2 ( A − 1 X T Y ) Σ W = A − 1 A = [ 1 σ 2 X T X + Σ p r i o r − 1 ] \begin{aligned} \mathcal P(\mathcal W \mid Data) \sim \mathcal N(\mu_{\mathcal W},\Sigma_{\mathcal W}) \\ \begin{cases} \mu_{\mathcal W} = \frac{1}{\sigma^2}(\mathcal A^{-1} \mathcal X^T \mathcal Y) \\ \Sigma_{\mathcal W} = \mathcal A^{-1} \\ \mathcal A = \left[\frac{1}{\sigma^2} \mathcal X^T\mathcal X + \Sigma_{prior}^{-1}\right] \end{cases} \end{aligned} P(W∣Data)∼N(μW,ΣW)⎩ ⎨ ⎧μW=σ21(A−1XTY)ΣW=A−1A=[σ21XTX+Σprior−1] - 基于
P
(
W
∣
D
a
t
a
)
\mathcal P(\mathcal W \mid Data)
P(W∣Data),给定未知样本
x
^
\hat x
x^,求解对应的标签信息
y
^
\hat y
y^的后验概率分布
P
(
y
^
∣
D
a
t
a
,
x
^
)
\mathcal P(\hat y \mid Data,\hat x)
P(y^∣Data,x^):
P ( y ^ ∣ D a t a , x ^ ) = ∫ W ∣ D a t a P ( W ∣ D a t a ) ⋅ P ( y ^ ∣ W , D a t a , x ^ ) d W = E W ∣ D a t a [ P ( y ^ ∣ W , D a t a , x ^ ) ] ∼ N ( x ^ T μ W , x ^ T ⋅ Σ W ⋅ x ^ + σ 2 ) \begin{aligned} \mathcal P(\hat y \mid Data,\hat x) & = \int_{\mathcal W \mid Data} \mathcal P(\mathcal W \mid Data) \cdot \mathcal P(\hat y \mid \mathcal W,Data,\hat x) d\mathcal W \\ & = \mathbb E_{\mathcal W \mid Data} \left[\mathcal P(\hat y \mid \mathcal W,Data,\hat x)\right] \\ & \sim \mathcal N \left(\hat x^T \mu_{\mathcal W} ,\hat x^T \cdot \Sigma_{\mathcal W} \cdot \hat x + \sigma^2\right) \end{aligned} P(y^∣Data,x^)=∫W∣DataP(W∣Data)⋅P(y^∣W,Data,x^)dW=EW∣Data[P(y^∣W,Data,x^)]∼N(x^TμW,x^T⋅ΣW⋅x^+σ2)
- 求解高维转换后
W
\mathcal W
W的后验概率分布
P
(
W
∣
D
a
t
a
)
\mathcal P(\mathcal W \mid Data)
P(W∣Data):
解决非线性问题的三种方式
上一节介绍,马文·明斯基认为感知机算法无法解决非线性问题,从而导致后续接近10年的神经网络方向的没落。关于非线性问题,传统的解决方法存在三种:
-
非线性转换(Non-Transformation)。其主要思想是:通过非线性转换,将原始的样本特征空间 X \mathcal X X转化为新的特征空间 Z \mathcal Z Z,转换的目标是在特征空间 Z \mathcal Z Z中将非线性问题转化为线性问题:
这里需要再次提到Cover定理:高维特征相较于低维特征更易线性可分。
ϕ : X ⇒ Z \phi:\mathcal X \Rightarrow \mathcal Z ϕ:X⇒Z -
核方法(Kernal Method):核方法本身和非线性转换方法是分不开的。根据 Cover \text{Cover} Cover定理,新的特征空间 Z \mathcal Z Z往往要高于原始的特征空间 X \mathcal X X。
但非线性转换在实践过程中往往存在一些弊端:- 非线性转换
ϕ
:
X
⇒
Z
\phi:\mathcal X \Rightarrow \mathcal Z
ϕ:X⇒Z的过程中,本身的计算可能是极为复杂的;
新特征空间Z \mathcal Z Z的产生需要极大的计算量。 - 假设已经得到了新特征空间 Z \mathcal Z Z,他的维度可能是极高的,甚至是无限维。这个计算代价同样是负担不起的;
- 同样是新特征空间 Z \mathcal Z Z的高维度,在特征维度增高的条件下,样本数量可能因维度扩张的脚步而出现维数灾难的情况发生。
而核方法的核心在于核技巧(Kernal Trick),其核心目的在于:通过核函数(Kernal Function)替代新特征 Z \mathcal Z Z的内积运算,从而减少了大量的运算过程。
- 假设
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)是特征空间
X
\mathcal X
X内的点,对应经过非线性转换得到对应点
z
(
i
)
,
z
(
j
)
z^{(i)},z^{(j)}
z(i),z(j):
x ( i ) , x ( j ) ∈ X z ( i ) = ϕ ( x ( i ) ) z ( j ) = ϕ ( x ( j ) ) x^{(i)},x^{(j)} \in \mathcal X \\ z^{(i)} = \phi(x^{(i)})\quad z^{(j)} = \phi(x^{(j)}) x(i),x(j)∈Xz(i)=ϕ(x(i))z(j)=ϕ(x(j)) - 构建核函数
κ
(
x
(
i
)
,
x
(
j
)
)
=
⟨
z
(
i
)
,
z
(
j
)
⟩
=
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
(
j
)
)
\kappa(x^{(i)},x^{(j)}) = \left\langle z^{(i)},z^{(j)}\right\rangle = \left[\phi(x^{(i)})\right]^T\phi(x^{(j)})
κ(x(i),x(j))=⟨z(i),z(j)⟩=[ϕ(x(i))]Tϕ(x(j)),如果该函数构建出来,可以通过原始特征空间直接得到转换后空间的内积结果,这种方式隐藏了非线性变换的复杂运算过程,并且也省掉了内积计算的运算过程,节省了大量运算。
对比以下‘非线性转换’和‘核方法’,它们的本意是相同的,均是通过将低维样本空间映射到高维,从而实现非线性问题的求解。不同点在于,非线性转换‘真的做了转换’,如何转换需要人为手动设计;
而核方法本身没有做转换,而是构建核函数,使其成为原始样本为输入,非线性转换后样本的内积作为结果。
- 非线性转换
ϕ
:
X
⇒
Z
\phi:\mathcal X \Rightarrow \mathcal Z
ϕ:X⇒Z的过程中,本身的计算可能是极为复杂的;
-
神经网络(Neural Network)。它的核心是通用逼近定理。这里依然以亦或分类问题为例:
在离散数学中,与( ∧ \land ∧),或( ∨ \vee ∨),非( ¬ \neg ¬)三种运算被称为基本运算;而亦或运算被称为复合运算。亦或运算使用基本运算表达结果如下:
x 1 ⊕ x 2 = ( ¬ x 1 ∧ x 2 ) ∨ ( x 1 ∧ ¬ x 2 ) x_1 \oplus x_2 = (\neg x_1 \land x_2) \vee (x_1 \land \neg x_2) x1⊕x2=(¬x1∧x2)∨(x1∧¬x2)
上述复合运算可以表示成如下步骤:
x 1 ⊕ x 2 = ( ¬ x 1 ∧ x 2 ) ⏟ s t e p − 1 ∨ ( x 1 ∧ ¬ x 2 ) ⏟ s t e p − 2 ⏟ s t e p − 3 x_1 \oplus x_2 = \underbrace{\underbrace{(\neg x_1 \land x_2)}_{step-1} \vee\underbrace{(x_1 \land \neg x_2)}_{step-2}}_{step-3} x1⊕x2=step−3 step−1 (¬x1∧x2)∨step−2 (x1∧¬x2)
假设使用有向图的形式去描述这个过程:
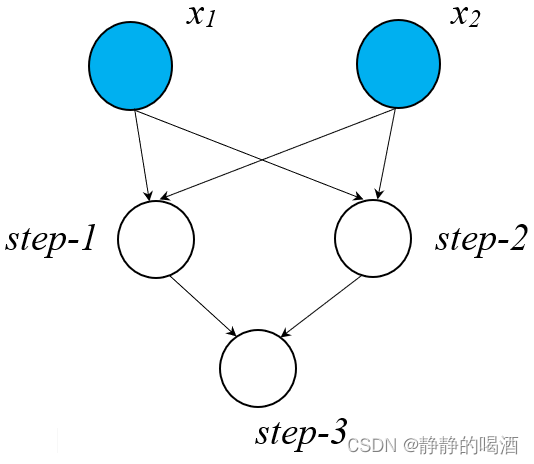
这明显是一个有向无环图,并且 step-1 , step-2 , step-3 \text{step-1},\text{step-2},\text{step-3} step-1,step-2,step-3
的主体运算均是基本运算,完全可以使用感知机算法进行线性可分。
step-1 \text{step-1} step-1在感知机算法中的激活函数表示如下:
step-1 = { 1 if x 1 = 0 , x 2 = 1 0 otherwise \text{step-1} = \begin{cases} 1 \quad \text{if } x_1 = 0,x_2 = 1 \\ 0 \quad \text{otherwise} \end{cases} step-1={1if x1=0,x2=10otherwise
同理, step-2 , step-3 \text{step-2},\text{step-3} step-2,step-3对应的激活函数分别表示为:
step-3 \text{step-3} step-3本身就是基本运算中的‘或’运算。
step-2 = { 1 if x 1 = 1 , x 2 = 0 0 otherwise step-3 = { 0 if x 1 = 0 , x 2 = 0 1 otherwise \text{step-2} = \begin{cases} 1 \quad \text{if } x_1 = 1,x_2 = 0 \\ 0 \quad \text{otherwise} \end{cases} \quad \text{step-3} = \begin{cases} 0 \quad \text{if } x_1 = 0,x_2 = 0 \\ 1 \quad \text{otherwise} \end{cases} step-2={1if x1=1,x2=00otherwisestep-3={0if x1=0,x2=01otherwise
并且从图中能够明显看出,亦或问题被表示成了一个嵌套的、复合函数。并且它的计算过程包含顺序,而这个顺序被图中的层级顺序所代替。
将上式进行归纳,构建一个神经网络,关于亦或问题表示如下:
-
x
1
,
x
2
x_1,x_2
x1,x2只能取
0
,
1
0,1
0,1两种条件,而求解目标是抑或问题:
x 1 ⊕ x 2 = { 1 x 1 ≠ x 2 0 x 1 = x 2 x_1 \oplus x_2 = \begin{cases} 1 \quad x_1 \neq x_2 \\ 0 \quad x_1 = x_2 \end{cases} x1⊕x2={1x1=x20x1=x2 - 将亦或问题分解为基本运算,并给予权重信息:包含非运算的元素赋权值
−
1
-1
−1;不包含非运算的元素赋权值
1
1
1;偏置项统一赋值
−
0.5
-0.5
−0.5。而激活函数依然使用符号函数:
sign ( a ) = { 1 if a > 0 0 otherwise \text{sign}(a) = \begin{cases} 1 \quad \text{if } a > 0 \\ 0 \quad \text{otherwise} \end{cases} sign(a)={1if a>00otherwise
示例:当 x 1 = 1 , x 2 = 0 x_1 =1,x_2 = 0 x1=1,x2=0时,验证以下这个前馈神经网络的最终结果:
step-1 : sign [ 1 × 1 + 0 × ( − 1 ) − 0.5 ] = 1 ( 0.5 > 0 ) step-2 : sign [ 1 × ( − 1 ) + 0 × 1 − 0.5 ] = 0 ( − 1.5 < 0 ) step-3 : sign [ 1 × 1 + 0 × 1 − 0.5 ] = 1 ( 0.5 > 0 ) \begin{aligned} \text{step-1 : }\text{sign} \left[1 \times 1 + 0 \times (-1) - 0.5\right] = 1 \quad (0.5 > 0) \\ \text{step-2 : }\text{sign} \left[1 \times (-1) + 0 \times 1 - 0.5\right] = 0 \quad (-1.5 < 0) \\ \text{step-3 : } \text{sign} \left[1 \times 1 + 0 \times 1 - 0.5\right] = 1 \quad (0.5 > 0) \end{aligned} step-1 : sign[1×1+0×(−1)−0.5]=1(0.5>0)step-2 : sign[1×(−1)+0×1−0.5]=0(−1.5<0)step-3 : sign[1×1+0×1−0.5]=1(0.5>0)
这完全满足亦或函数的描述,那么这样的模型结构以及对应的模型参数(权值、偏置项)就可以表示亦或分类问题。
其他的情况也可以试验,这里就不多赘述了。
上述针对亦或分类问题构建了一个完整的前馈神经网络:

该图相比于上面的计算过程存在一些差别。
- 首先出现了一个新的结点:偏置。
- 中间的白色点也不在表示与或非产生的运算步骤,取而代之的是包含权重信息、偏置项信息的线性运算,经过激活函数后产生的结果。
也就是说,相比于计算过程图,白色结点不再具有实际的逻辑意义,只有包含抽象意义的计算过程。
这个就是机器学习中层次化的体现。这种网络结构也称为多层感知机,名字也很朴素,就是由若干个感知机堆叠在一起产生的模型结构。也称为前馈神经网络(Feedforward Neural Network)。
从这个点也能看出,前馈神经网络依然是‘频率派’的代表模型。
因为在整个模型结构的构建以及模型参数的赋予(这里的模型参数的试出来的,不是学习出来的,仅是一个简单的例子)和概率没有关联关系。并且这里的模型参数(权重信息、偏置项)被假设为一个未知的常量。而不是通过后验概率的方式进行求解。个人认为最有说服力的特征就是h 1 , h 2 , h 3 h_1,h_2,h_3 h1,h2,h3所表示的三个结点均不是随机变量。在之前介绍的很多模型。如Sigmoid信念网络、受限玻尔兹曼机中所有的结点,无论是观测变量还是隐变量,它们均是随机变量。
因而区别于概率图,通常称层次化的神经网络图,如
MLP,CNN,RNN
\text{MLP,CNN,RNN}
MLP,CNN,RNN等称为计算图(
Computational Graph
\text{Computational Graph}
Computational Graph)
相关参考:
马文·明斯基——百度百科
非线性问题的三种解决方法







![LeetCode[1046]最后一块石头的重量](https://img-blog.csdnimg.cn/img_convert/ee9d1d25f27a29710e5b58444b087993.png)