目录
一.移位操作符
1.左移操作符
2.右移操作符
二.位操作符
1.位运算基本知识
2.位运算的巧妙运用
三.其他操作符
1.算术操作符
2.单目操作符
3.关于逻辑操作符
四.表达式求值
隐式类型转换
(1)整形提升(短整型家族数据的二进制序列补位转换)
(2).算术转换
一.移位操作符
<< 左移操作符
>> 右移操作符
注:移位操作符的操作数只能是整数。
1.左移操作符
移位规则:
左边抛弃、右边补0.
2.右移操作符
移位规则:
首先右移运算分两种:
(1). 逻辑移位
左边用0填充,右边丢弃
(2). 算术移位
左边用原该值的符号位填充,右边丢弃
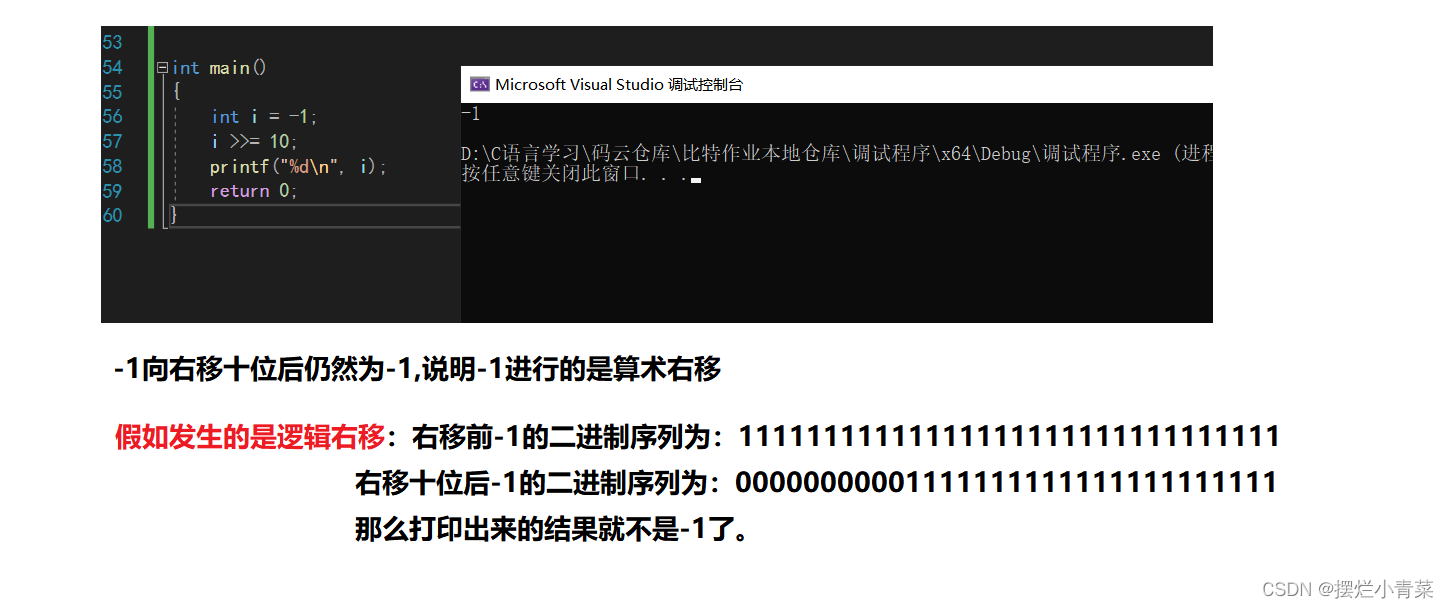
在vs2022编译器中,整形数据的右移操作执行的是算术右移,即移动后,左边的二进制位用原数据的符号位来填充。
二.位操作符
1.位运算基本知识
&
|
^按位与
按位或
按位异或注:他们的操作数必须是整数。
按位与&:两个整数对应的二进制位如果同为1则该位的运算结果为1,否则为0
按位或|:两个整数对应的二进制位只要有一个1则该位的运算结果为1,否则为0
按位异或^:两个整数对应的二进制位不同则该位的运算结果为1,否则为0
位运算按位与,按位或,按位异或都满足交换律和结合律。位运算的交换律和结合律有十分巧妙的运用。
2.位运算的巧妙运用
leetcode645. 错误的集合问题描述:
leetcode链接:645. 错误的集合 - 力扣(Leetcode)
集合
s包含从1到n的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合丢失了一个数字 并且 有一个数字重复 。给定一个数组
nums代表了集合S发生错误后的结果。请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
题解函数接口定义:int* findErrorNums(int* nums, int numsSize, int* returnSize)
nums是给定的数组的首地址
numsSize是数组的元素个数
returnSize是记录返回的数组(需要动态内存分配函数来开辟)的元素个数的变量的地址
注意给定的数组是乱序的
本题的其中的一个求解办法就是用位运算:
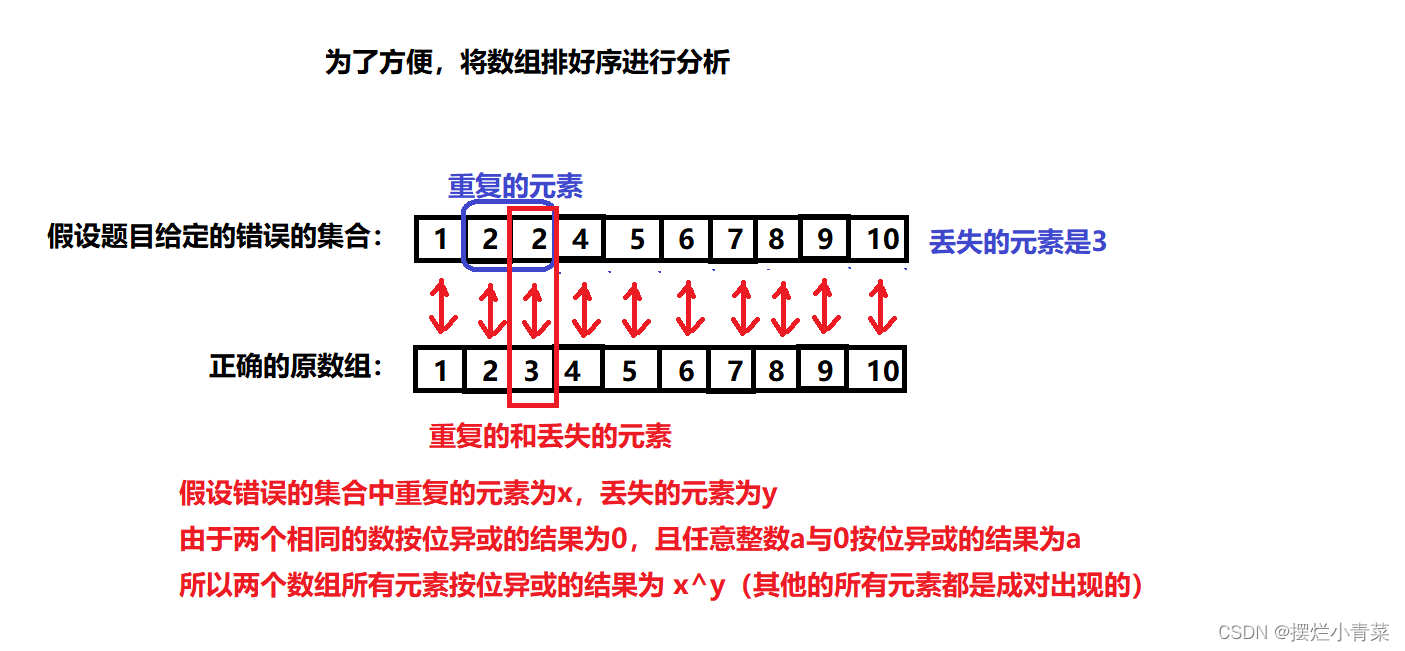
第一步:利用按位异或运算的可交换性和可结合性可以得到丢失的数字和重复的数字两个数字的按位异或的结果。
我们将题目给定的错误的数组和正确的原数组两个数组中的所有元素进行按位异或的运算。
int Norsum = 0;
int i = 0;
for (i = 0; i < numsSize; i++)
{
Norsum ^= nums[i];
Norsum ^= (i + 1);
}Norsum中便记录了数组中重复的数字和丢失的数字按位异或的结果
Norsum的二进制序列相当于记录了重复的数字和丢失的数字的二进制序列的不同位
第二步:
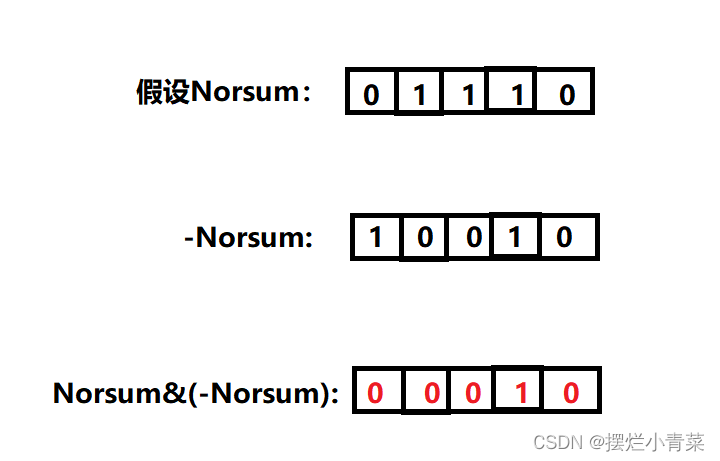
取出Norsum中的最低位的1记录在lowbit变量中:
int Norsum = 0; int i = 0; for (i = 0; i < numsSize; i++) { Norsum ^= nums[i]; Norsum ^= (i + 1); } int lowbit = Norsum &(-Norsum);此时lowbit就记录了重复的数字和丢失的数字两个正整数二进制序列最低的不同位。
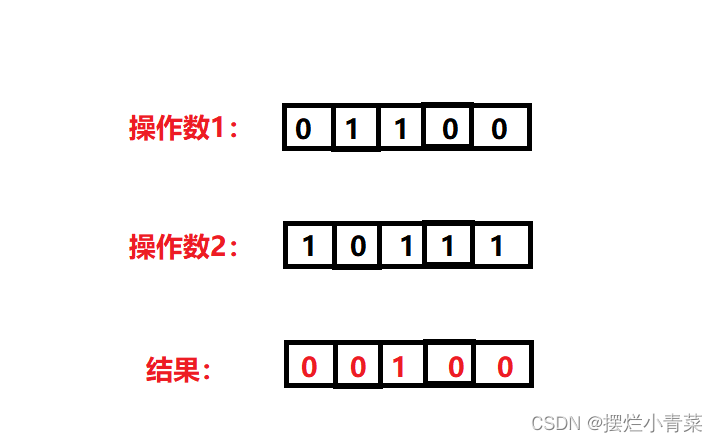
第三步:将题目给定的数组和正确的原数组的所有元素逐一与lowbit进行按位&运算,由于lowbit的二进制序列只有一位为1,所以每次按位与运算的结果要么为0要么等于lowbit。
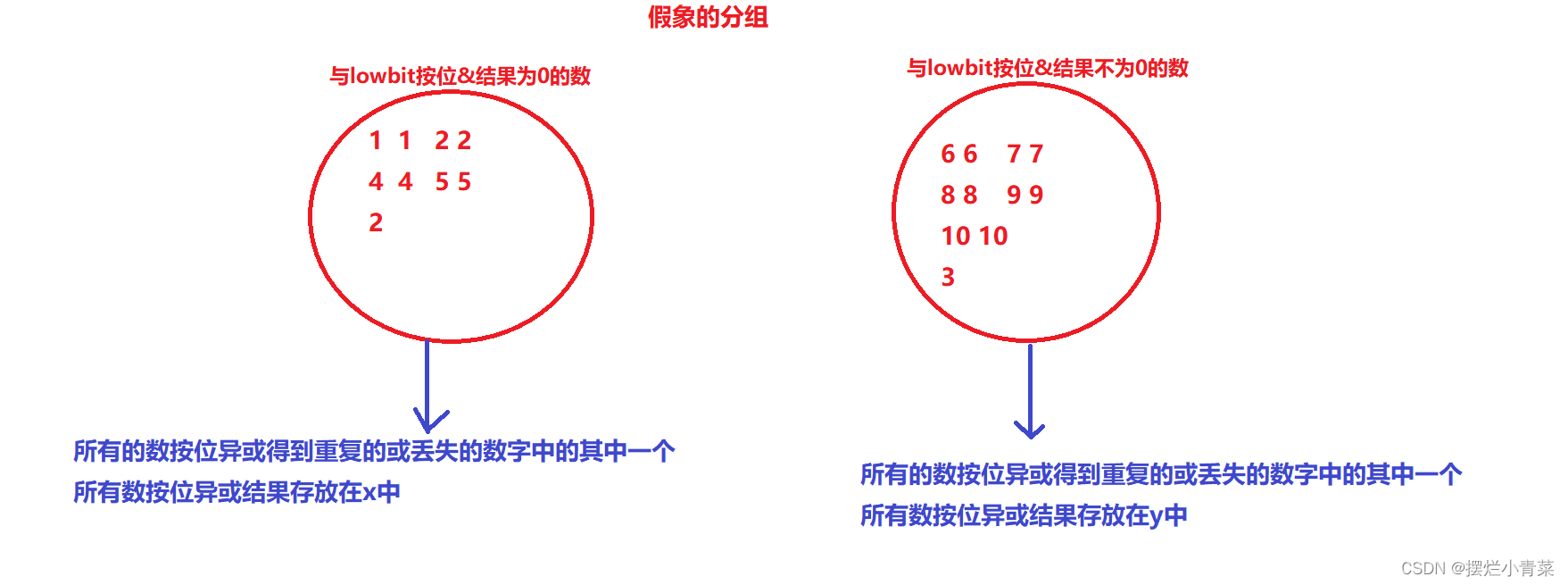
int Norsum = 0; int i = 0; for (i = 0; i < numsSize; i++) { Norsum ^= nums[i]; Norsum ^= (i + 1); } int lowbit = Norsum &(-Norsum); int x = 0; int y = 0; for (i = 0; i < numsSize; i++) { if (0 == lowbit & nums[i]) { x ^= nums[i]; } else { y ^= nums[i]; } } for (i = 0; i < numsSize; i++) { if (0 == lowbit & (i + 1)) { x ^= (i + 1); } else { y ^= (i + 1); } }两组元素分别按位异或后结果存放在x和y两个变量中,由于相同的元素必然分到同一组,重复的元素和丢失的元素必然被分到不同组,所以最终x和y分别为丢失的元素和重复的元素的其中一个,但是无法确定x,y与丢失元素和重复元素的具体对应关系,最后只需再遍历一次nums数组确定这个对应关系即可。
int* Return = NULL; if ((Return = (int*)malloc(sizeof(int) * 2)) == NULL) { printf("malloc failed\n"); exit(0); }开辟一个两个元素的数组来存储结果:Return[0]存放重复的元素
Return[1]存放丢失的元素
再遍历一次nums数组确定x和y与丢失的元素和重复的元素的对应关系。
int flag = 1; 用flag来标记x是否为重复的元素 for (i = 0; i < numsSize; i++) 确定x是否存在于nums数组中。 { if (x == nums[i]) { Return[0] = x; Return[1] = y; flag = 0; } } if (flag) { Return[0] = y; Return[1] = x; }题解代码:
int* findErrorNums(int* nums, int numsSize, int* returnSize) { int Norsum = 0; int i = 0; for (i = 0; i < numsSize; i++) { Norsum ^= nums[i]; Norsum ^= (i + 1); } int lowbit = Norsum &(-Norsum); int x = 0; int y = 0; 利用lowbit将两组元素分成两组分别以按位异或的方式存入x和y中。 for (i = 0; i < numsSize; i++) { if (0 == (lowbit & nums[i])) { x ^= nums[i]; } else { y ^= nums[i]; } } for (i = 0; i < numsSize; i++) { if (0 == (lowbit & (i + 1))) { x ^= (i + 1); } else { y ^= (i + 1); } } int* Return = NULL; if ((Return = (int*)malloc(sizeof(int) * 2)) == NULL) { printf("malloc failed\n"); exit(0); } int flag = 1; 用flag来标记x是否为重复的元素 for (i = 0; i < numsSize; i++) 确定x是否存在于nums数组中。 { if (x == nums[i]) { Return[0] = x; Return[1] = y; flag = 0; } } if (flag) { Return[0] = y; Return[1] = x; } *returnSize = 2; return Return; }
三.其他操作符
1.算术操作符
+ - * / %
1. 除了 % 操作符之外,其他的几个操作符可以作用于整数和浮点数。
2. 对于 / 操作符如果两个操作数都为整数,执行整数除法。而只要有浮点数执行的就是浮点数除法。
3. % 操作符的两个操作数必须为整数。返回的是整除之后的余数。
2.单目操作符
!
-
+
&
sizeof
~
--
++*
(类型)
逻辑反操作
负值
正值
取地址
操作数的类型长度(以字节为单位)
对一个数的二进制按位取反
前置、后置--
前置、后置++间接访问操作符(解引用操作符)
强制类型转换
注意sizeof(类型名)时括号不能省
3.关于逻辑操作符
#include <stdio.h> int main() { int i = 0,a=0,b=2,c =3,d=4; i = a++ && ++b && d++; printf("a = %d\n b = %d\n c = %d\nd = %d\n", a, b, c, d); return 0; } 程序输出的结果是什么?逻辑操作符尤其要注意的是逻辑短路规则:
比如:
对于逻辑与 &&(且)表达式:a&&b,若表达式a为假(值为0),则计算机不会计算表达式b,整个表达式的结果为0;
对于逻辑或 || (或)表达式:a||b ,若表达式a为真(值为非0),则计算机不会计算表达式b,整个表达式结果为1;
代码段中的表达式i = a++ && ++b && d++;
由于a++是先访问a的值再完成a的自增,所以a++表达式的值为0,基于逻辑短路规则,&&后面的逻辑表达式不会再计算,i的值被赋为0,a自增为1,b,d的值不变,因此打印的结果为a=1,b=2,c=3,d=4;
四.表达式求值
表达式求值的顺序一部分是由操作符的优先级和结合性决定。
同样,有些表达式的操作数在求值的过程中可能需要转换为其他类型。只要有表达式,我们就要考虑类型转换的问题。
隐式类型转换
(1)整形提升(短整型家族数据的二进制序列补位转换)
C的整型算术运算总是至少以缺省整型类型的精度来进行的.
为了获得这个精度,表达式中的字符和短整型等(字节数小于整形int)操作数在使用之前被转换为普通整型(二进制序列补到与int同位数),这种转换称为整型提升。
整型提升的意义:
表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度(二进制序列的长度)。
通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int(二进制序列补位),然后才能送入CPU去执行运算。
对于有符号的短整型家族数据,整形提升时二进制序列高位补符号位。
对于无符号的短整型家族数据,整形提升时二进制序列高位补0。
相关实例:
阅读代码预测输出结果:
int main()
{
char a = 0xb6;
short b = 0xb600;
int c = 0xb6000000;
if(a==0xb6)
printf("a");
if(b==0xb600)
printf("b");
if(c==0xb6000000)
printf("c");
return 0;
}0xb6和0xb600都是整形数据存入a和b都会发生截断
0xb6对应的二进制序列为: 00000000000000000000000010110110
0xb600对应的二进制序列为: 00000000000000001011011000000000
0xb6截断后存入a中的序列: 10110110(最高位被视为符号位)
0xb600截断后存入b中的序列:1011011000000000(最高位被视为符号位)
a==0xb6比较时a发生整形提升高位补1,结果不再相同.
b==0xb600比较时a发生整形提升高位补1,结果不再相同.
所以最后只打印c
相关实例:
阅读代码预测输出结果:
int main() { char c = 1; printf("%u\n", sizeof(c)); printf("%u\n", sizeof(+c)); printf("%u\n", sizeof(-c)); return 0; }
+c和-c都是运算表达式.
因此sizeof(+c),sizeof(-c)中c会发生整形提升算出来结果为4个字节。(VS2022整形为4个字节)。
相关实例:
阅读代码预测输出结果:
int main()
{
unsigned char a = 200;
unsigned char b = 100;
unsigned char c = 0;
c = a + b;
printf(“%d %d”, a+b,c);
return 0;
}200截断存入a中的二进制序列为:1100 1000
100截断存入b中的二进制序列为:0110 0100
c= a+b 运算时a和b都要发生整形提升,由于是无符号数所以高位补0。
a+b整形提升后运算结果为:00000000000000000000000100101100
截断后存入c中的二进制序列: 00101100(转换为十进制为44)
a+b和c打印前a,b,c也要发生整形提升。
最后打印结果为:300 44
(2).算术转换
且某个操作符的各个操作数的大小如果都大于或等于整形,且各个操作数属于不同的类型,那么除非其中一些操作数的转换为另一个操作数的类型,否则操作就无法进行。这种转换称为算术转换。
算术转换的原则是小的,精度低的数据类型向更大,精度更高的数据转换(向上转换原则)。
相关实例:
阅读代码预测输出结果:
int main()
{
int i;
i--;
if (i > sizeof(i))
{
printf(">\n");
}
else
{
printf("<\n");
}
return 0;
}sizeof()操作符返回的结果为无符号整形(unsigned int) .
注意i为全局变量,会默认初始化为0.
所以i和sizeof(i)比较时i会发生算术转换,转换为无符号数,而i原本为-1,二进制序列为三十二个1,所以转换为无符号数后是一个非常大的正数。所以程序会输出>