目录
问题描述:
实现代码与解析:
递归:
原理思路:
迭代(前序):
思路原理:
问题描述:
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
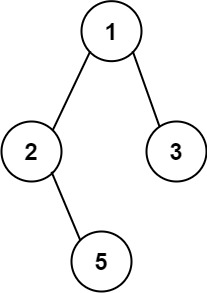
输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
实现代码与解析:
递归:
class Solution {
public:
void traversal(TreeNode* cur,vector<int> path,vector<string>& result)
{
//先将结点加入路径中
path.push_back(cur->val);
//到了叶子结点,记录整条路径,返回
if(cur->left==NULL&&cur->right==NULL)
{
string paths;//记录整条路径
//依据输出格式
for(int i=0;i<path.size()-1;i++)
{
paths+=to_string(path[i]);
paths+="->";
}
paths+=to_string(path[path.size()-1]);//记录最后一个结点
result.push_back(paths);
return;//返回
}
if(cur->left) traversal(cur->left,path,result);
if(cur->right) traversal(cur->right,path,result);
return;
}
vector<string> binaryTreePaths(TreeNode* root)
{
vector<int> path;//记录路径
vector<string> result;//记录结果
if(root==NULL) return result;
traversal(root,path,result);
return result;
}
};精简版:
class Solution {
public:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val);
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result);
if (cur->right) traversal(cur->right, path + "->", result);
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};原理思路:
用一个数组path记录路径,一个数组result记录最终结果,每到一个结点就将结点值放入数组中,若碰到了叶子结点, 就将此时数组记录的路径传入结果result中,注意按照题目给的格式传入。精简版的代码就直接定义path为string类型的,每到一个结点就直接加一个"->"的符号,也是可以的,相对来说代码更简洁一些,还是很巧妙的。这里还用到了 to_string() 函数:
to_string() 函数:将数字常量转换为字符串,返回值为转换完毕的字符串。
我们判断完是否为叶子结点(也就是左右子树为空)后,需要再判断一下左右子树是否有一侧为空的,再决定向左子树还是右子树走,如下图:

或者我们还按之前题目的遍历一样,走到结点后再判断是否为空,若为空,在记录结点前直接返回就可以,这样我们就不用在走之前判断一下了,就如下图的同样情况下: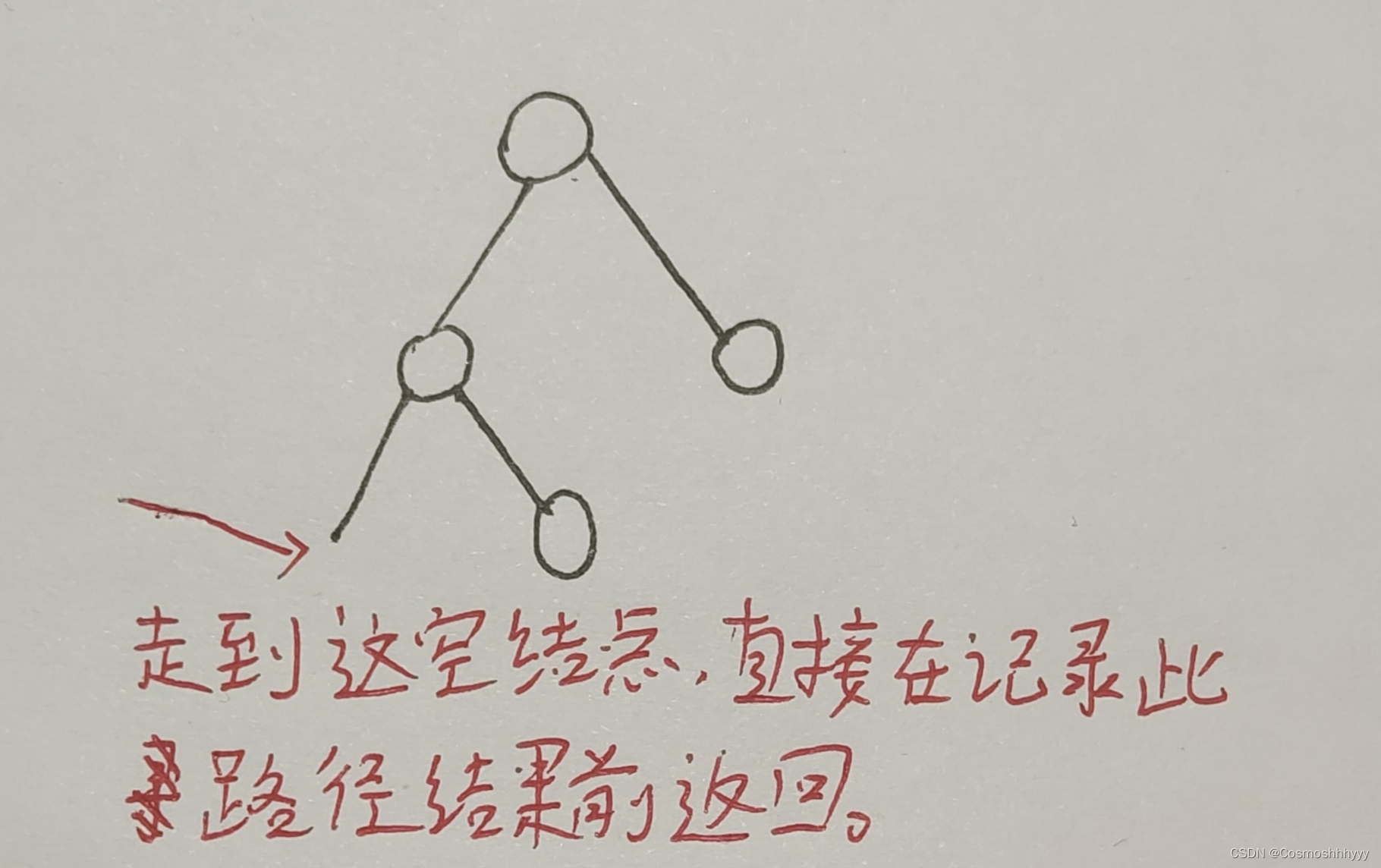
这种处理方式的代码如下:
class Solution {
public:
void traversal(TreeNode* cur, string path, vector<string>& result)
{
if(cur==NULL) return;//这里就是和上面代码的不同,也是可以通过的
path += to_string(cur->val);
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
traversal(cur->left, path + "->", result); //不同处
traversal(cur->right, path + "->", result); //不同处
}
};显然第一种处理方法应该好一点。其实就是解决了一下一些人包括我自己的疑问,为什么我们之前有的题就是第二种返回方式,而这个题用的第一种返回方式,其实这题加上第二种方式也是可以的,只是具体实现代码有少些区别而已,只要我们想明白代码的执行过程,对于不同思路的具体写法就有了更深的认知,也就能在写不同的题的时候,明白我们用不同思路解题时那些可用,那些不可用,那些方法更好。
这个递归方法也还有别的写法,就是将path以引用的方式传入,不过我们要在每次返回的时候把该结点再移出路径,因为我们要折回去向别的方向走了嘛。上面的代码直接用的是值传递,当返回时,path自动就变为上一层的值了,也就是这样写可以省略移出的这个步骤而已,思路是一样的,只是不同的写法而已,以值传递写虽然更简洁,但也需要你能够熟悉并理解它隐藏和省略的步骤。下面给出引用传递写此题的代码:
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
{
path.push_back(cur->val);
if (cur->left == NULL && cur->right == NULL) {
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back(); //不同处
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back(); // 不同处
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
vector<int> path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};迭代(前序):
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root)
{
vector<string> result;//接收结果
stack<TreeNode*> s1;//记录结点
stack<string> s2;//记录遍历过的路径
if(root==NULL) return result;
s1.push(root);
s2.push(to_string(root->val));
while(!s1.empty())
{
string path;//记录路径
path+=s2.top();//取出该结点的路径
s2.pop();
TreeNode* temp=s1.top();
s1.pop();//弹出结点
if(temp->left==NULL&&temp->right==NULL) result.push_back(path);//到了叶子结点,path记入结果
if(temp->right)
{
s1.push(temp->right);
s2.push(path+"->"+to_string(temp->right->val));
}
if(temp->left)
{
s1.push(temp->left);
s2.push(path+"->"+to_string(temp->left->val));
}
}
return result;
}
};思路原理:
其实就是用栈模拟了一下递归的步骤,这里看出还是递归好写,这里记录路径的步骤和遍历结点的步骤是一一对应的,因为记录路径的栈就是记录的对应结点的路径,当结点入栈,对应的路径就入栈,当结点出栈,对应的路径就出栈,记住这个规则,我们在写代码的时候就不会乱了,把上面代码的部分找出放在下面,你就知道我说的是什么意思了。
//一一对应之处,只截取了部分代码
//第一处
stack<TreeNode*> s1;//记录结点
stack<string> s2;//记录遍历过的路径
//第二处
s1.push(root);
s2.push(to_string(root->val));
//第三处
string path;//记录路径
path+=s2.top();//取出该结点的路径
s2.pop();
TreeNode* temp=s1.top();
s1.pop();//弹出结点
//第四处
s1.push(temp->right);
s2.push(path+"->"+to_string(temp->right->val));//与当前路径相加
//第五处
s1.push(temp->left);
s2.push(path+"->"+to_string(temp->left->val));