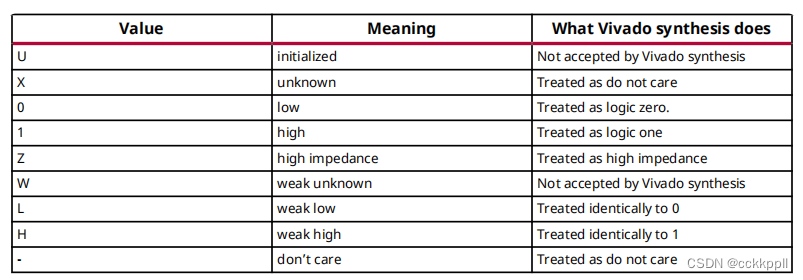
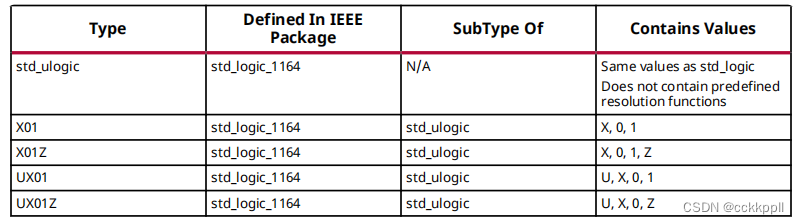
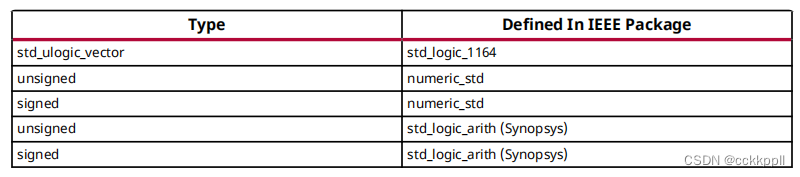
某些VHDL数据类型是预定义包的一部分。有关他们在哪里的信息编译,以及如何加载它们,请参阅VHDL预定义包。该类型在IEEE std_logic_1164包中定义。
VHDL整数类型
整数类型是预定义的VHDL类型。Vivado合成在32位上实现一个整数默认情况下。为了更紧凑的实现定义可应用值的精确范围,其中类型MSB在8到15的范围内。您还可以利用预定义的自然类型和正类型,重载整数类型
VHDL多维数组类型
Vivado synthesis支持VHDL多维数组类型。
建议:尽管尺寸数量没有限制,但描述的数量不超过三维。
多维数组类型的对象可以传递给函数并在组件中使用实例化。可以描述的多维数组类型的对象是信号,
常量和变量。
完全约束阵列类型编码示例
数组类型必须在所有维度上都受到完全约束。
subtype WORD8 is STD_LOGIC_VECTOR (7 downto 0);
type TAB12 is array (11 downto 0) of WORD8;
type TAB03 is array (2 downto 0) of TAB12;
Array Declared as a Matrix Coding Example
You can declare an array as a matrix.
subtype TAB13 is array (7 downto 0,4 downto 0) of STD_LOGIC_VECTOR (8
downto 0);
Multi-Dimensional Array Signals and Variables
Coding Examples
1. Make the following declarations:
subtype WORD8 is STD_LOGIC_VECTOR (7 downto 0);
type TAB05 is array (4 downto 0) of WORD8;
type TAB03 is array (2 downto 0) of TAB05;
signal WORD_A : WORD8;
signal TAB_A, TAB_B : TAB05;
signal TAB_C, TAB_D : TAB03;
constant CNST_A : TAB03 := (
("00000000","01000001","01000010","10000011","00001100"),
("00100000","00100001","00101010","10100011","00101100"),
("01000010","01000010","01000100","01000111","01000100"));
2. You can now specify:
• A multi-dimensional array signal or variable:
TAB_A <= TAB_B; TAB_C <= TAB_D; TAB_C <= CNST_A;
• An index of one array:
TAB_A (5) <= WORD_A; TAB_C (1) <= TAB_A;
• Indexes of the maximum number of dimensions:
TAB_A (5) (0) <= '1'; TAB_C (2) (5) (0) <= '0'
• A slice of the first array
TAB_A (4 downto 1) <= TAB_B (3 downto 0);
• An index of a higher level array and a slice of a lower level array:
TAB_C (2) (5) (3 downto 0) <= TAB_B (3) (4 downto 1); TAB_D (0) (4) (2
downto 0)
\\ <= CNST_A (5 downto 3)
3. Add the following declaration:
subtype MATRIX15 is array(4 downto 0, 2 downto 0) of
STD_LOGIC_VECTOR (7 downto 0);
signal MATRIX_A : MATRIX15;
4. You can now specify:
• A multi-dimensional array signal or variable:
MATRIXA <= CNST_A
• An index of one row of the array:
MATRIXA (5) <= TAB_A;
• Indexes of the maximum number of dimensions
MATRIXA (5,0) (0) <= '1';
VHDL记录类型代码示例
•记录类型的字段也可以是记录类型。
•常量可以是记录类型。
•记录类型不能包含属性。
•Vivado合成支持记录信号的聚合分配。以下代码snippet就是一个例子:
type mytype is record field1 : std_logic; field2 : std_logic_vector (3
downto 0);
end record;