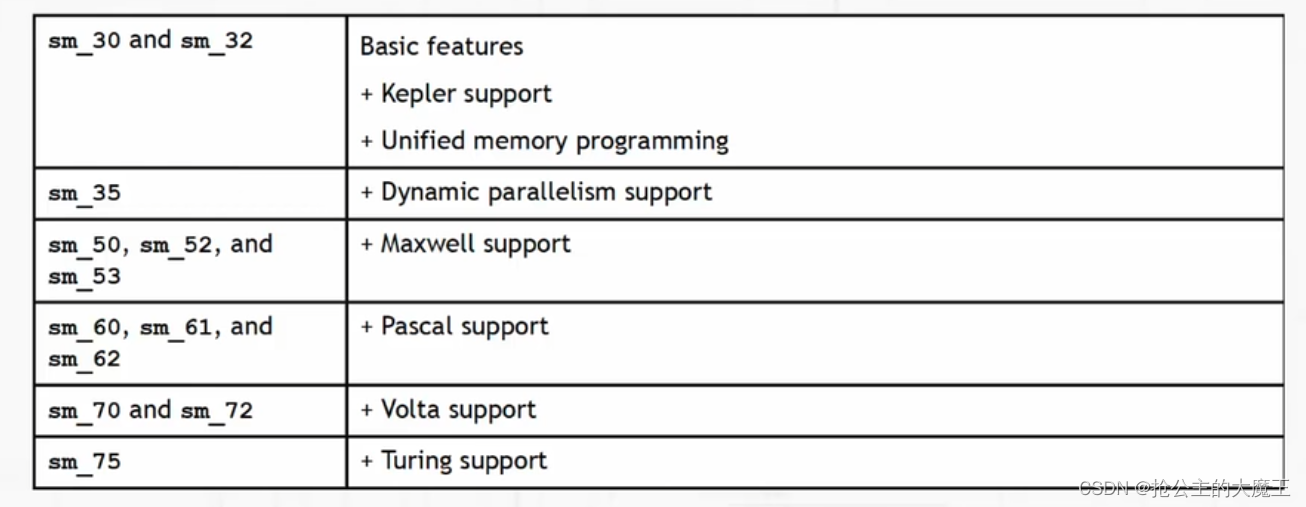
一、算法原理

假设点（x0, y0, z0）, 平面方程为 mx + ny + sz + d = 0

过点（x0, y0, z0），且垂直平面的直线方程为
$$\frac{x-x0}{m}=\frac{y-y0}{n}=\frac{z-z0}{s}$$

点到平面的投影就是上述直线与平面的交点，注意到直线的参数方程为
$$x=mt+x0,y=nt+y0,z=st+z0$$
代入平面方程求解t
$$t=-\frac{mx+ny+sz+d}{m\ast m+n\ast n+s\ast s}$$
将t带入到平面方程得到投影。。结合代码看易于理解。

二、代码

import numpy as np
import open3d as o3d


def plane(pcd, normal_vector):
    """
    Args:将点云投影到平面
        pcd:  点云数据
        normal_vector:  方程法向量 mx + ny + sz + d = 0  传入[m , n, s, d]
    Returns: 投影后的点云数据
    """
    plane_seeds = []   # 保存投影后的点云数据
    # 获取平面系数
    m = normal_vector[0]
    n = normal_vector[1]
    s = normal_vector[2]
    d = normal_vector[3]
    # 将点云转换为数组
    points = np.asarray(pcd.points)
    for xyz in points:
        x, y, z = xyz
        """
        t = -(m*x + n*y + s*z + d) / (m*m + n*n + s*s)  # 计算参数方程参数
        """
        t = -(m*x + n*y + s*z + d) / (m*m + n*n + s*s)  # 计算参数方程参数
        """
        xi = m*t + x    # 计算x的投影
        yi = b*t + y    # 计算y的投影
        zi = s*t + z    # 计算z的投影
        """
        xi = m * t + x  # 计算x的投影
        yi = n * t + y  # 计算y的投影
        zi = s * t + z  # 计算z的投影
        plane_seeds.append([xi, yi, zi])  # 将投影后的点云添加到数组中

    plane_cloud = o3d.geometry.PointCloud()  # 使用numpy生成点云
    plane_cloud.points = o3d.utility.Vector3dVector(plane_seeds)  # points numpy数组

    return plane_cloud


if __name__ == '__main__':
    # -------------------读取点云数据------------------------
    cloud_size = 1000
    a = np.random.ranf(cloud_size * 3).reshape(-1, 3) * 1024
    pcd = o3d.geometry.PointCloud()  # 使用numpy生成点云
    pcd.points = o3d.utility.Vector3dVector(a)  # points numpy数组
    # pcd = o3d.io.read_point_cloud('res/bunny.pcd')   # 读取兔子点云
    plane_cloud = plane(pcd, [1, 0, 1, 0])  # 获得投影后的点云数据
    # ------------------ 可视化点云 -----------------
    plane_cloud.paint_uniform_color([1, 0, 0.0])  # 渲染颜色
    o3d.visualization.draw_geometries([pcd, plane_cloud])

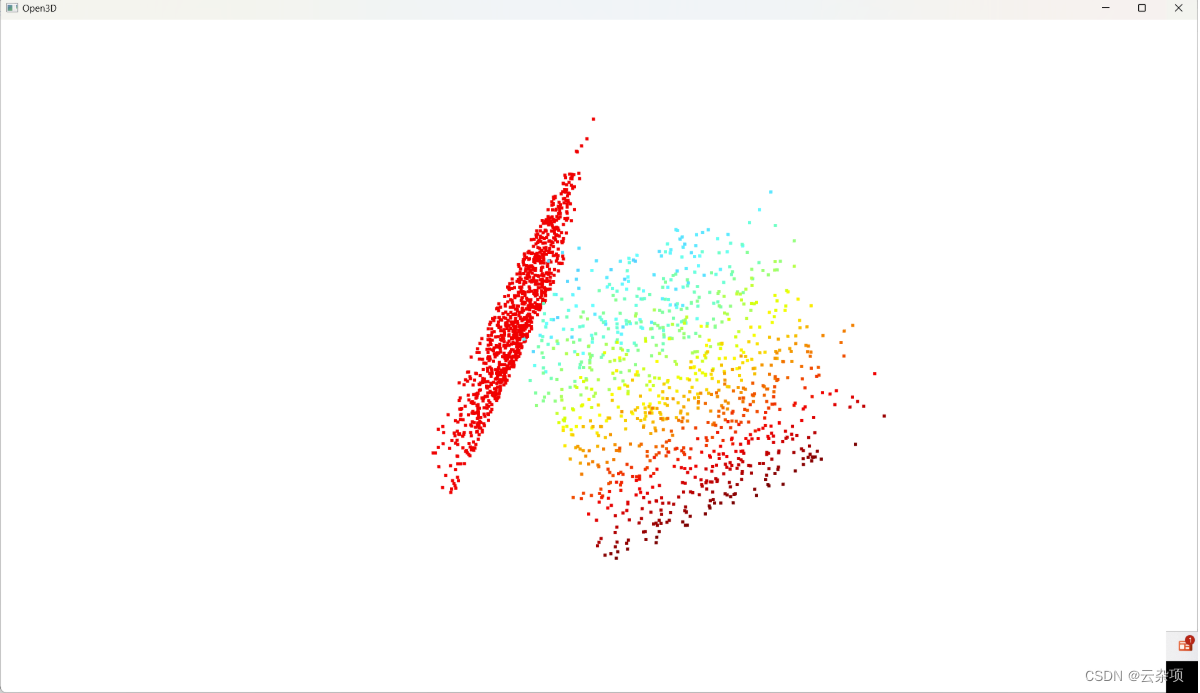
三、结果展示

1.原点云

2.点云数据向x + z = 0投影

四、相关数据

参考文章

pclpy 参数模型投影：pclpy 参数模型投影-CSDN博客

点到平面的投影：点到平面的投影 - 知乎 (zhihu.com)