摘要：近年来，基于深度学习的轴承故障诊断得到了较为系统的研究。但是，这些方法中的大多数的成功在很大程度上依赖于大量的标记数据，而这些标记数据在实际生产环境中并不总是可用的。如何在有限的数据条件下训练出鲁棒的轴承故障诊断模型，并使其在复杂工况下工作良好，仍然是一个挑战。针对这一问题，提出了一种基于模型不可知元学习的元学习故障诊断方法（MLFD）。该方法首先将不同工况下的原始信号转换为时频图像，然后根据元学习协议对原始信号进行随机采样，形成多层次故障诊断任务。MLFD模型在元训练过程中，基于已知工况下的多个故障分类任务，通过优化初始化参数获取先验知识，利用学习到的知识实现未知工况下的快速准确的少样本轴承故障诊断。为了综合评价该方法的性能，基于美国凯斯西储大学轴承故障基准测试系统，对不同的工业场景进行了仿真实验，实验结果证明了MLFD在解决复杂工况下少样本故障分类问题上的优越性。

一、问题背景

基于DL的故障诊断领域近年来取得了长足的进展，但依赖于大量的标记训练数据和昂贵的计算资源来训练网络，严重限制了其在故障诊断中的应用潜力。因为大量数据的获取需要由大量传感器收集，并且标记数据需要大量人力，导致高成本投资，且工况数据存在长尾现象，故障数据与正常数据相比有限且难以获取。
为了解决如何收集足够的样本来训练鲁棒的故障诊断模型的问题，目前主流的方法通常包括三类：数据扩充（DA）、迁移学习（TL）和少样本学习（FSL）。
目前基于FSL的故障诊断研究还处于起步阶段，现有的研究主要采用基于度量的少样本方法，其分类和泛化性能依赖于选择好的特征提取器和精确的距离度量，需要足够的经验和实验。

二、本文贡献

本文贡献如下：

1. 提出了一种基于元学习框架的少样本轴承故障诊断方法，该方法通过从已知工况数据中学习元知识，能够快速适应新任务，实现未知复杂工况下的高精度故障分类。
2. 提出了一种基于N-way K-shot 协议和开源轴承数据集的MLFD模型任务组织方法，满足了基于任务的训练要求，保证了MLFD模型能够从多个不同的任务中学习到更一般的故障信息。
3. 综合评价了MLFD的性能，实验结果表明，MLFD具有自学习能力，适合解决复杂制造场景下的少样本故障诊断问题。

三、基础知识

3.1.元学习

从多个相关任务中学习先前的经验，并依赖于获得的经验来提高其在目标任务上的表现，而无需从头开始训练。元学习旨在基于"学会学习"元知识 ω 的能力产生一种通用算法，使模型在应用于不同分布的任务时具有更强的泛化能力和更快的自适应能力。元学习的目标描述如下：

值得注意的是，元学习中的 ω 是在学习过程中跨多个任务学习的，最好的 ω 可以尽可能地减少新任务的损失L。
除了上述与传统方法的区别外，元学习还引入了一系列新的术语。元学习是从人类学习过程中演化而来的，其本质是从多个任务中学习先验知识，对此已有大量的研究。在将元学习的求解转化为优化问题的方法中，MAML是最具代表性的方法。MAML的核心思想是在元训练过程中采用梯度下降法获得模型的初始参数，在应用于数据有限的不可见任务时，通过几个梯度步长更新已有参数以获得最佳性能。此外，MAML算法具有模型不可知性和通用性，适用于不同类型的模型和不同的领域，如回归、分类和强化学习等。MAML已经成功地应用于许多领域：少样本、图像分类、强化学习、语音识别和煤烟密度识别。

元学习术语：

四、本文方法

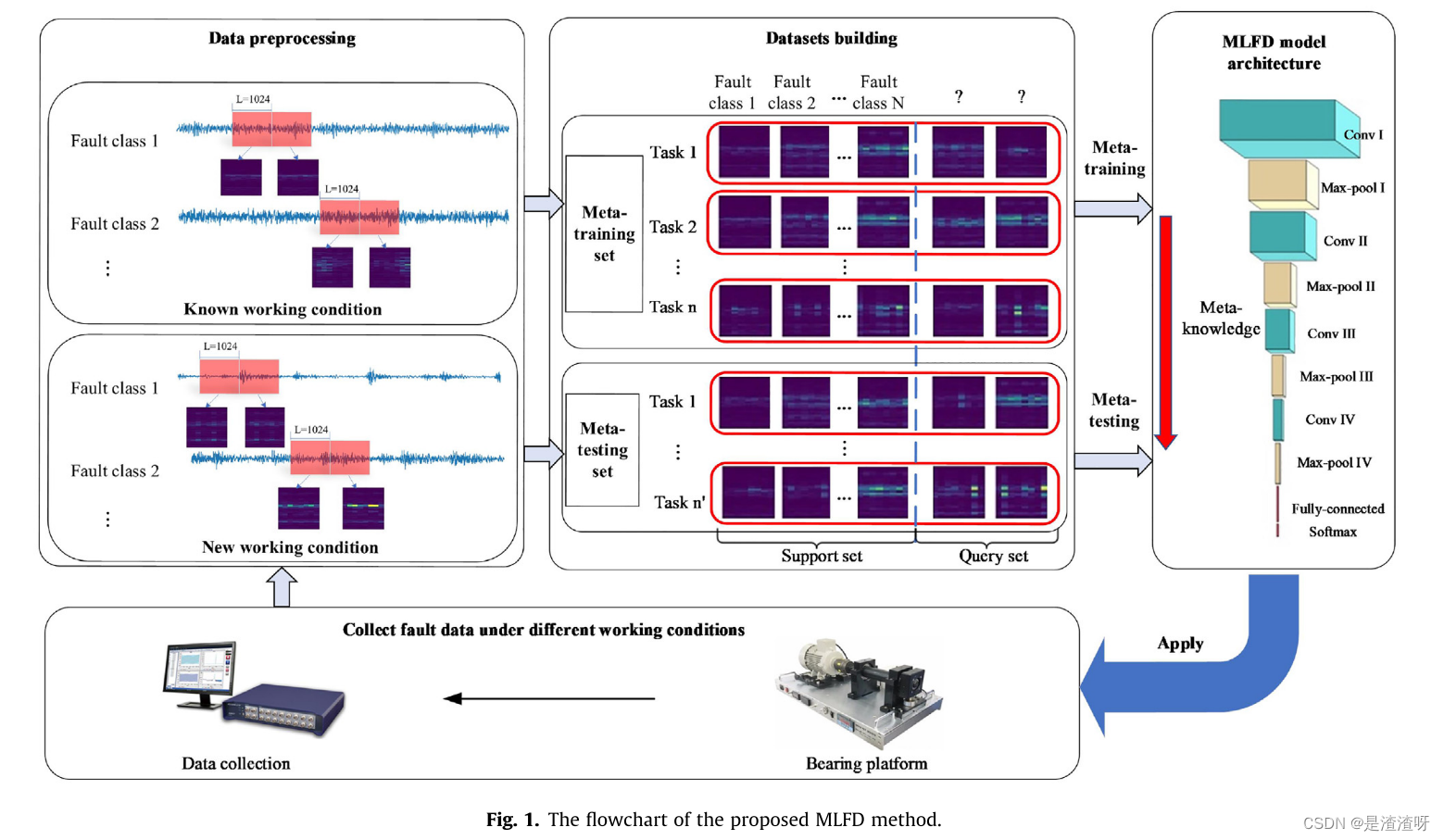
新工况下轴承故障的识别是一个典型的少样本分类问题，传统的DL模型难以解决。为此，我们应用先进的元学习理论，提出了基于MAML框架的MLFD方法，流程如图1所示。
整个过程分为四个步骤：

1. 采集不同工况下的故障样本；
2. 将其转换为时频图像；
3. 利用时频图像为元学习准备任务；
4. MLFD模型实现新工况下的少样本故障分类
   

4.1.数据预处理

利用加速度传感器采集轴承振动信号是故障诊断中最常用的信号采集方法之一。由于原始振动信号仅表示一维时域，通常采用短时傅里叶变换（STFT）将原始数据转换为TFI，以全面获取时频域信息。得到的TFI如图1左上方所示，x轴、y轴和亮度分别代表时间、频率和频域幅度。
STFT通过乘以窗函数 ψ(t) 将信号 f(t) 分解成多个段，并在时间轴上的 τ 处对每个段应用快速傅立叶变换（FFT）。短时傅立叶变换的数学公式如下：

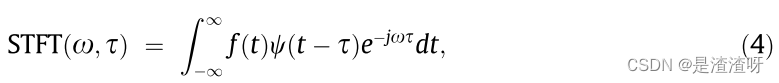
并且为了减少频谱泄漏，这里使用大小为1024的汉宁窗。

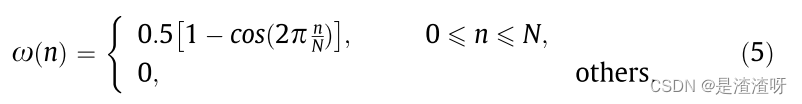
4.2.数据集构建

可用于组织元学习任务的数据集应满足两个基本条件：

1. 数据集应包含不同类型的故障以构建多个少样本任务。
2. 标记样本以计算指标。

本文提出了一种基于开源轴承数据集的MLFD任务组织方法，根据N路K样本协议进行少样本故障诊断。如图1所示，为了确保MLFD从多个不同任务中学习到更一般的故障信息，我们使用已知工况和新工况的TFI分别准备元训练集、元验证集和元测试集。

每个集合包含10种类型的故障，并且在执行10路1-shot（或5-shot）分类任务时将每个TFI视为一个shot。每个任务的目标是用给定的数据正确地分类10种类型的故障。

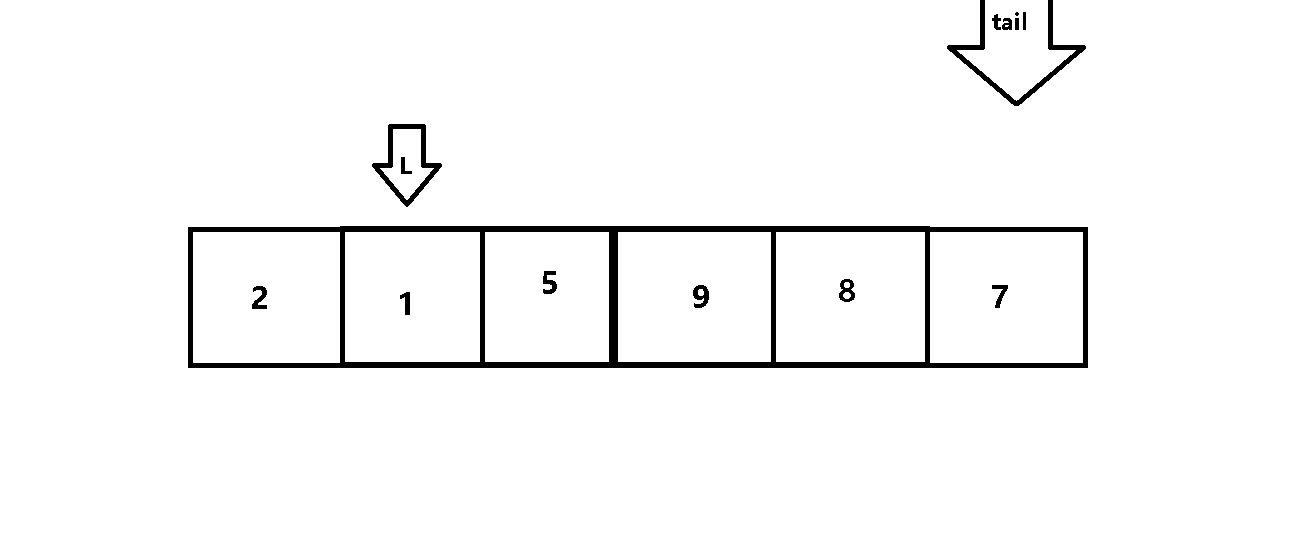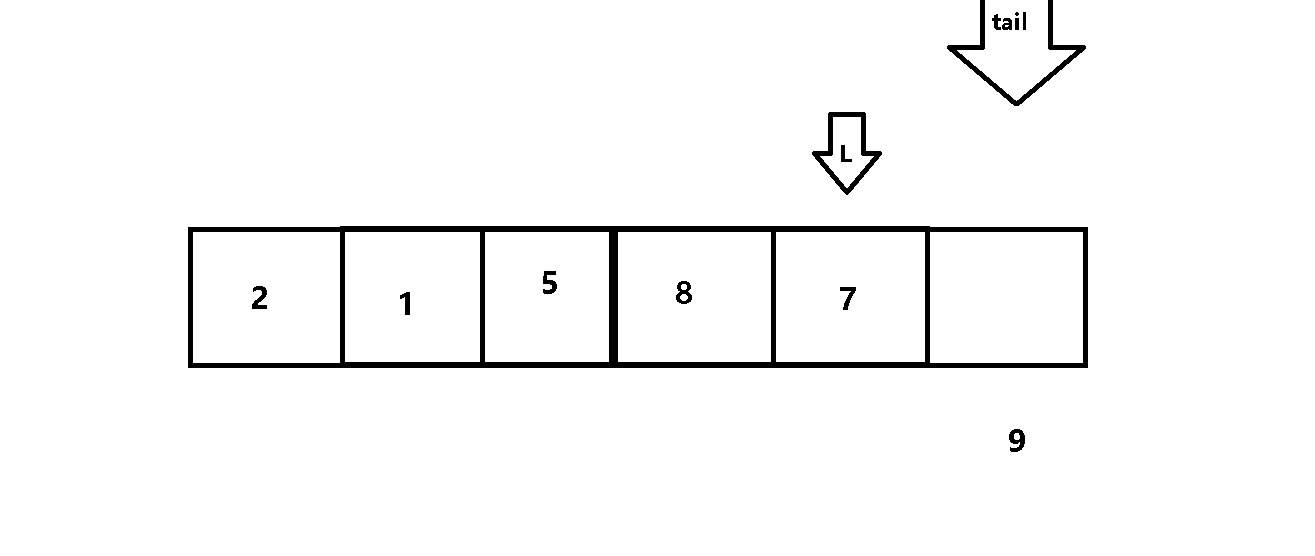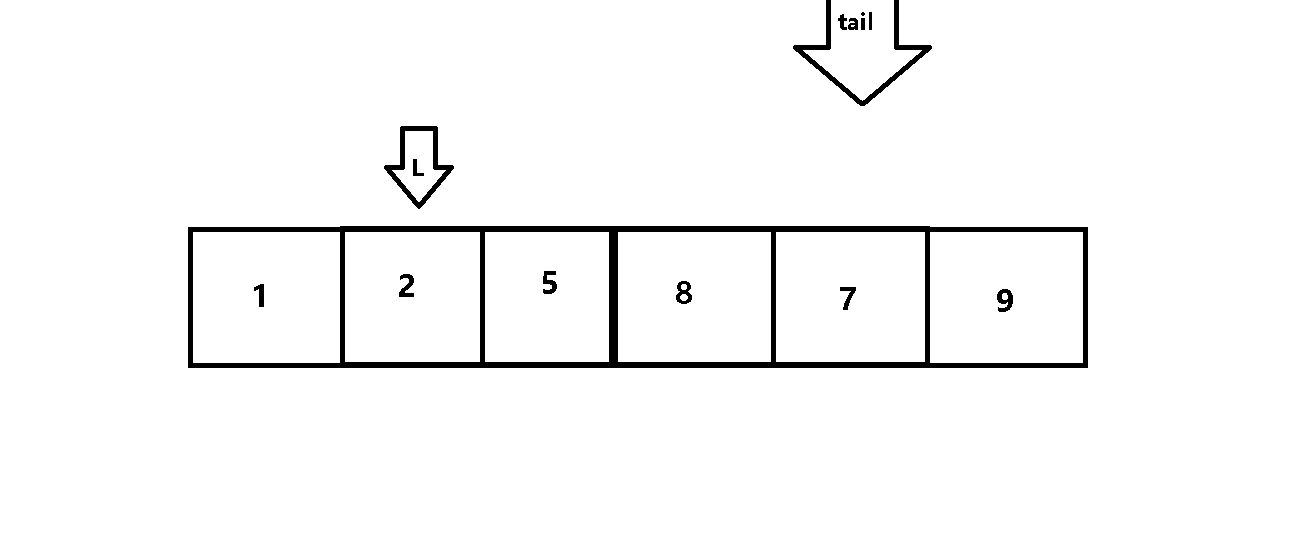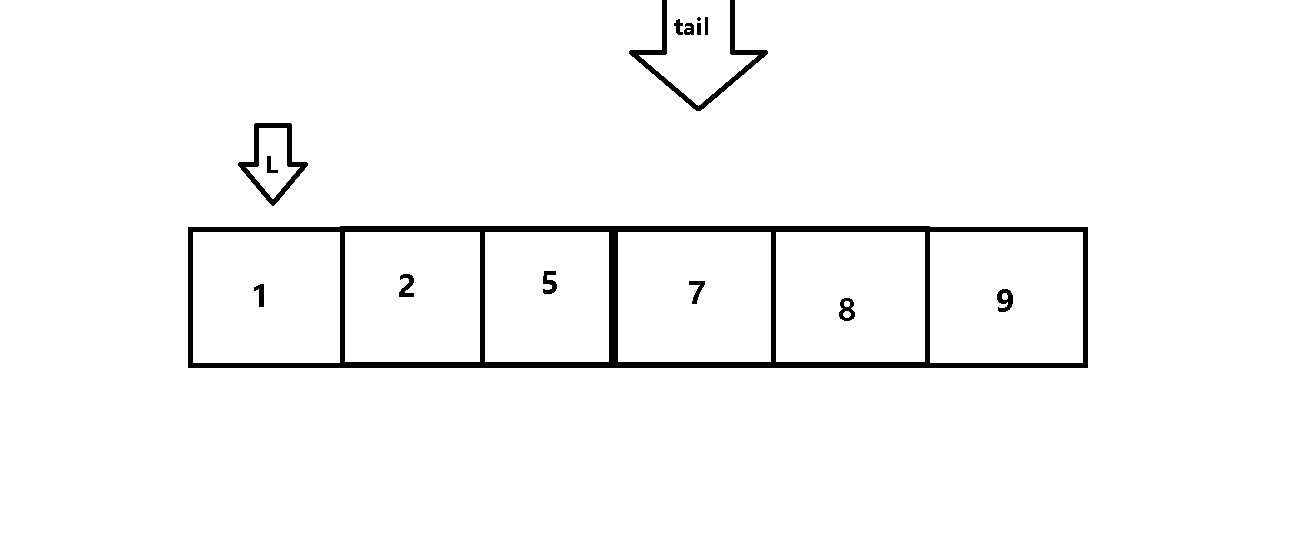
在元训练集的准备过程中，从每种故障类型中随机抽取 M个TFI，用 K个TFI 组成一个10路K-shot支持集，剩余的TFI组成相应的查询集.每个任务的支持集用于训练故障分类模型并提供相应损失的反馈，训练后的查询集数据用于评价模型的性能。如此反复多次，就可以得到整个元训练阶段的任务。

元验证集和元测试集的任务也是以同样的方式得到的，只不过是提取新工况数据。

4.3.网络详细信息

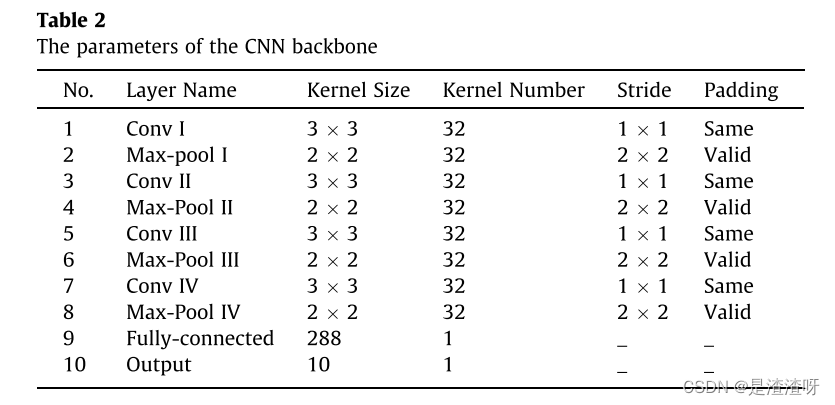
为了避免在少故障诊断中的过拟合，我们提出的MLFD模型的主干与MAML的主干相同，MAML是具有4个卷积层的简单卷积神经网络（CNN），如图1右上方所示。CNN的输入为84*84个三通道RGB的TFI，每个样本依次经过卷积、批量归一化和max-pooling操作，重复4次，直到满足全连通层。然后利用softmax函数对得到的前几层提取的断层特征图进行分类，CNN的参数如表2所示。

4.4.元学习算法流程

1. 随机初始化参数，采样任务批
2. 对于每个任务，都先采样支持集；
3. 再n次梯度下降；
4. 然后采样查询集的数据；
5. 所有任务都完成上述过程后，再在查询集上计算所有任务总的损失；
6. 然后更新模型参数并采样元测试阶段的任务批。
7. 重复上述操作，直至最后的参数，使用最终的模型在元测试任务上预测故障类别并计算分类准确率！！！

五、实验

略