目录

 一.插入排序

1.算法描述：

2.实现思路：

3.时间复杂度：

代码如下： 

二.希尔排序 （插入排序的优化升级）

1.算法描述：

2.实现思路：

3.时间复杂度： 

代码如下：  

三.选择排序

1.算法思想：

2.实现思路：

3.时间复杂度：

 代码如下：

 四.冒泡排序

1.算法思想：

2.实现思路：

3.时间复杂度：

 代码如下：

---

一.插入排序

1.算法描述：

假设排为升序，从第二个数据逐次向后遍历，遇到更小的数据时，就将其向后平移。

2.实现思路：

设定两个指针 i 和 q ；i 负责整体数据遍历，q 负责处理遇到更小数据的情况 。

3.时间复杂度：

   O(n^2) 

动态图解析：

代码如下： 

//插入排序
void insersort(int* pq, int k)
{
	for (int i = 1; i < k; i++)           （这里设定从下标为 1 处开始，默认至少两个数据）
	{
		for (int q = i; pq[q] < pq[q - 1]; q--)
		{
			swap(&(pq[q]), &(pq[q - 1]));
		}
	}
}

二.希尔排序 （插入排序的优化升级）

1.算法描述：

假设排为升序，希尔排序的算法思想与插入排序基本一致，都是依次遍历，遇到更小数据向后平移，但是插入排序每次遍历一个数据，我们称之为步长gap 为 1 ， 所以当gap为 1 的时候，进行一次插入排序，就能得到我们想要的结果，可是当数据量庞大的时候，gap = 1的情况下，时间成本也随之升高。

所以希尔排序在gap = 1之前进行多次预排序，即引入gap = 6 ;gap = 4; gap = 3等多次插入排序，使得在进行gap = 1的最后一次插入排序前，随着gap 的值越来越接近1 ，原数据已经接近最后的排序结果 ，这样一来，gap = 1的插入排序的时间复杂度由原先的O(n^2)，大幅缩减，特殊情况下，甚至可以降到O(n)的效果。

2.实现思路：

设定一个gap，依据原数据量，给定gap 不同的、依次减小的多个值，并以gap 作为步长进行多次插入排序，直至gap = 1的最后一次插入排序的完成。

3.时间复杂度： 

O(n^(1.3-2))

动态图解析：

代码如下：  

//希尔排序
void ShellSort(int* pq,int k )
{
	int gap = (k / 3) + 1;
	for (; gap >= 1;gap = (gap/3)+1)
	{
		int i = 0;
		for (int ki = 0; i < k-gap; i++)
		{
			int temp = pq[i+gap];
			for ( ki = i+gap; ki-gap >= 0; ki -= gap)
			{
				if (pq[ki-gap] < temp)
				{
					pq[ki] = pq[ki-gap];
				}
				else
					break;
			}
			pq[ki] = temp;
		}
		if (gap == 1)
			break;
	}
}

三.选择排序

1.算法思想：

第一次从待排序组中选出最小和最大值分别平移至排序组的首尾（假设排升序）

下一次排序组剔除上一组的最大和最小值，然后重复筛选出最大和最小值，以此类推

2.实现思路：

用两个变量（head,last）控制每次遍历的范围，用变量L进行遍历。

3.时间复杂度：

    O(n^2)

动图解析：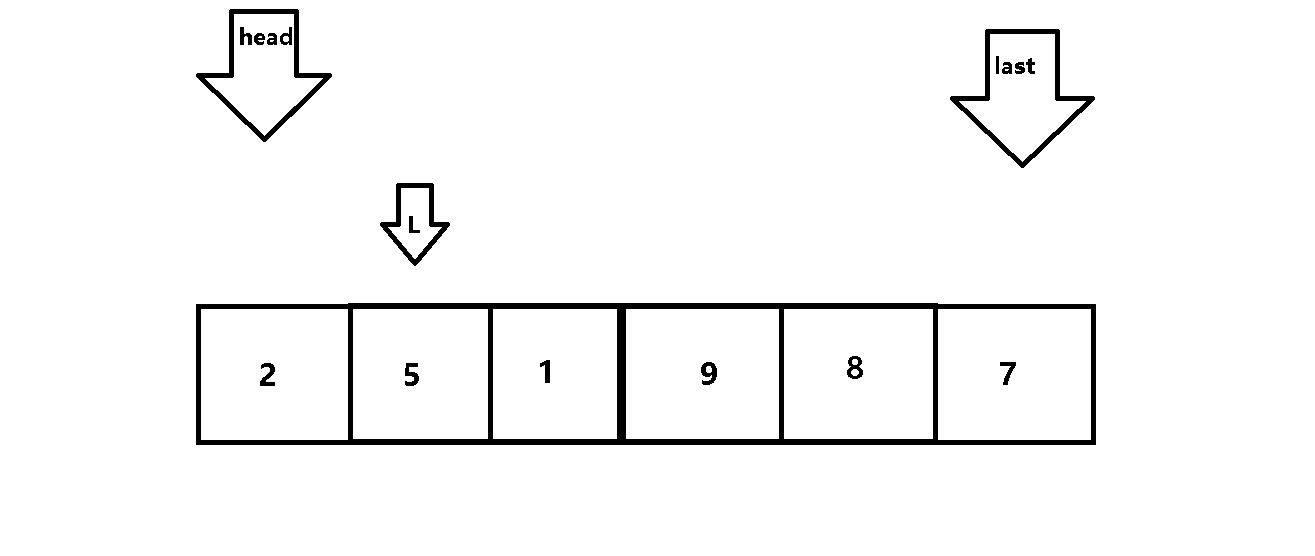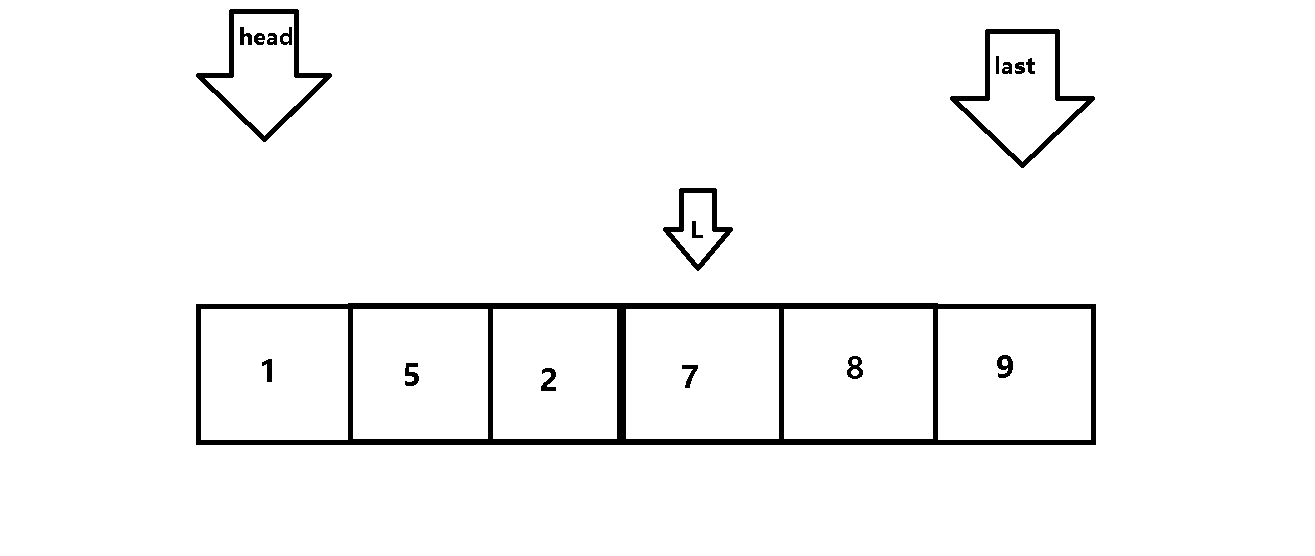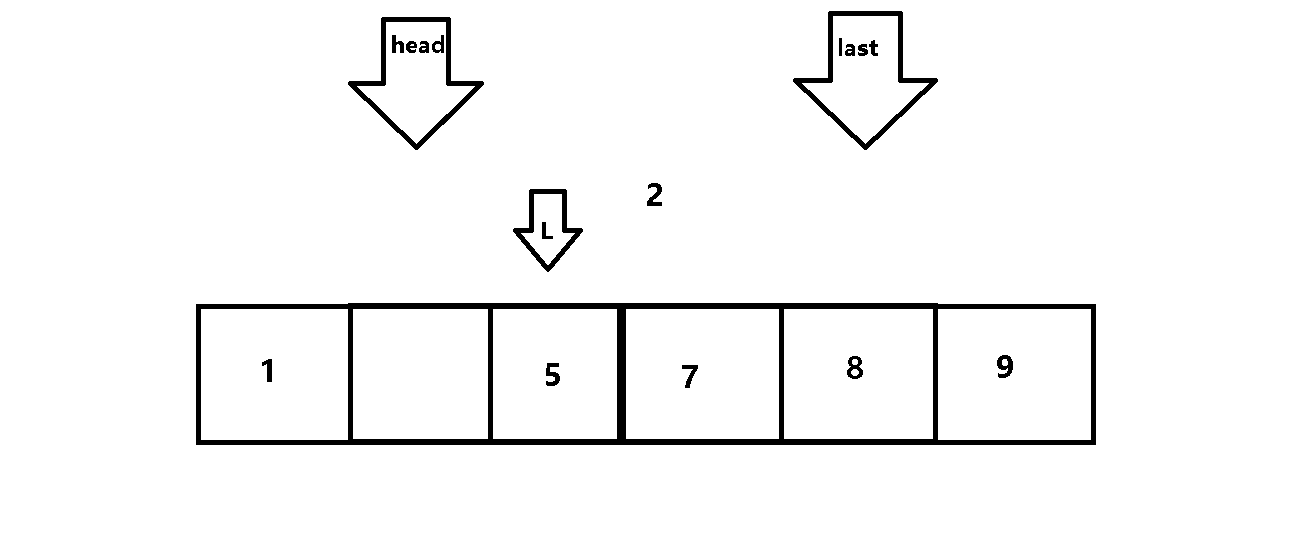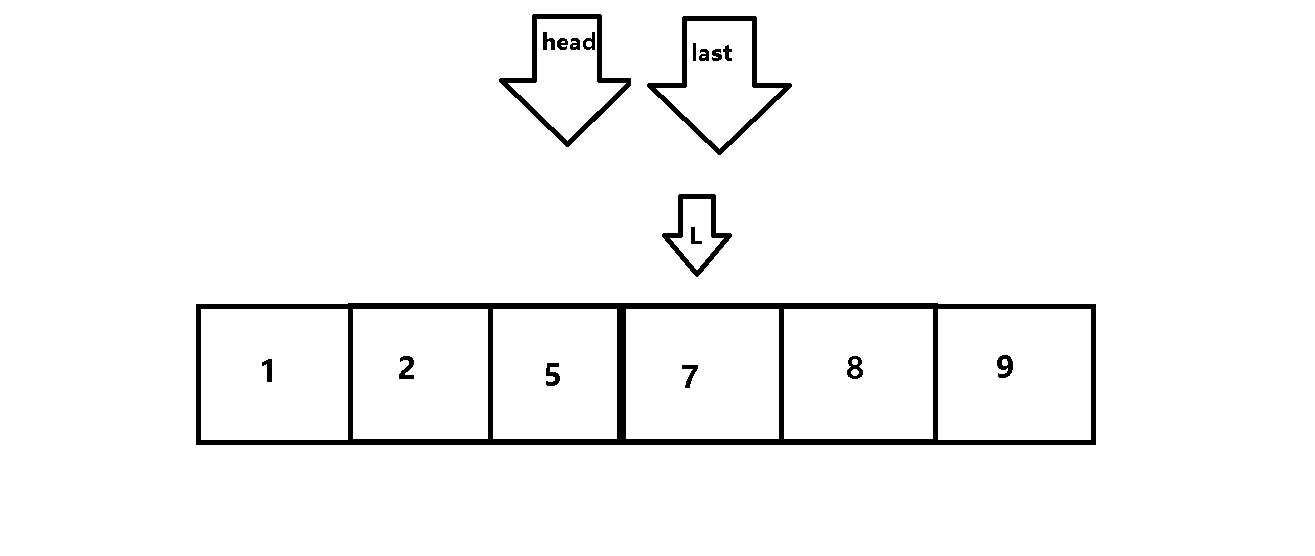

 代码如下：

//选择排序
void SelectSort(int* pq, int k)
{
	int min = 0, max = k - 1;
	int head = 0, last = k-1;
	for (int L = head; head<last;head++,last--)
	{
		L = head;
		for (min = head,max = last; L<=last;L++)
		{
			if (pq[L] < pq[min])
				swap(&pq[min], &pq[L]);
			if (pq[L] > pq[max])
				swap(&pq[max], &pq[L]);
		}
	}
}

 四.冒泡排序

1.算法思想：

将第一个和第二个元素比较，若第一个大于第二个（假设排升序），则交换，然后用第二个（大的）与第三个比较，若第三个大，则交换，以此类推，遍历到最后一个元素时，队尾一定是这组排序数中最大的元素，第二轮排序时将他剔除掉，找出第二大的元素，以此类推。

2.实现思路：

用变量tail 来设定每次遍历的范围，用变量L 来进行前后元素的比较

3.时间复杂度：

O(n^2)

动图解析：

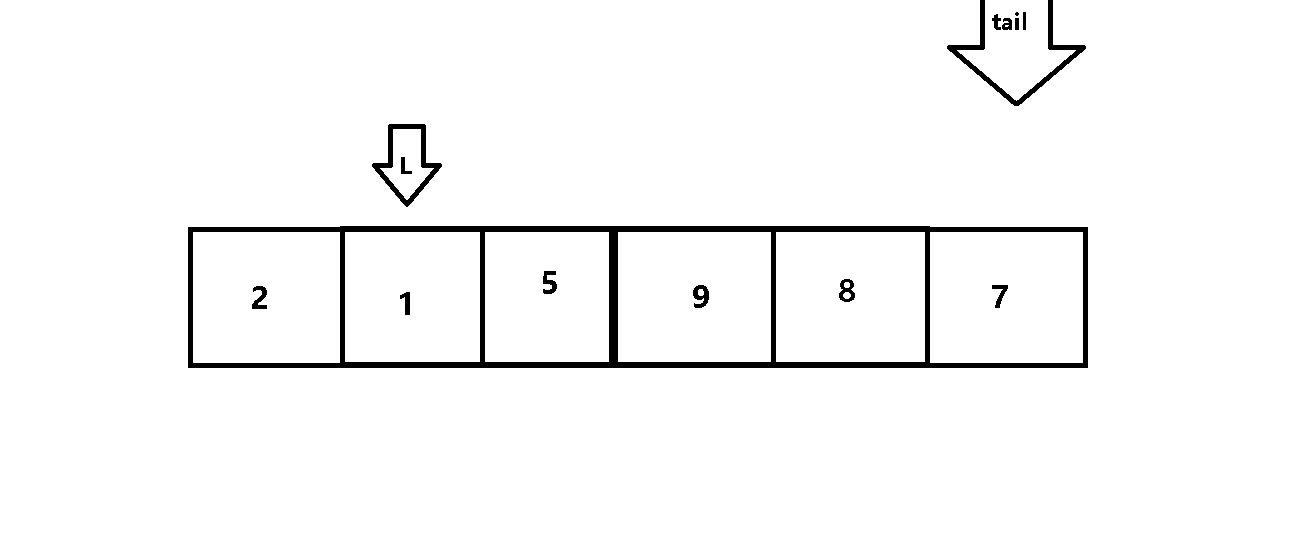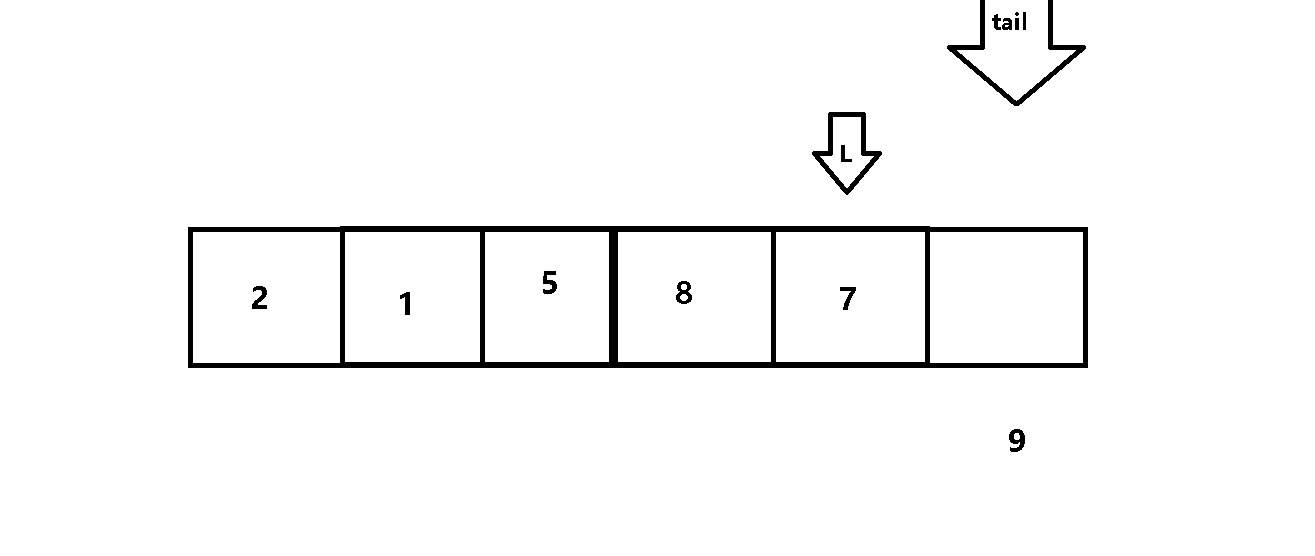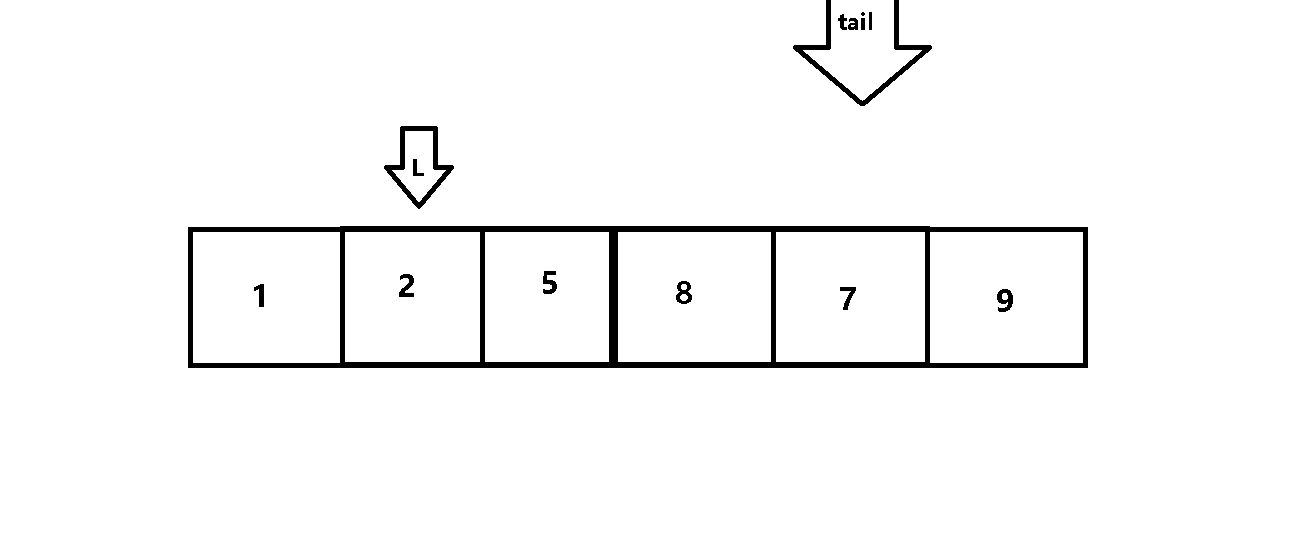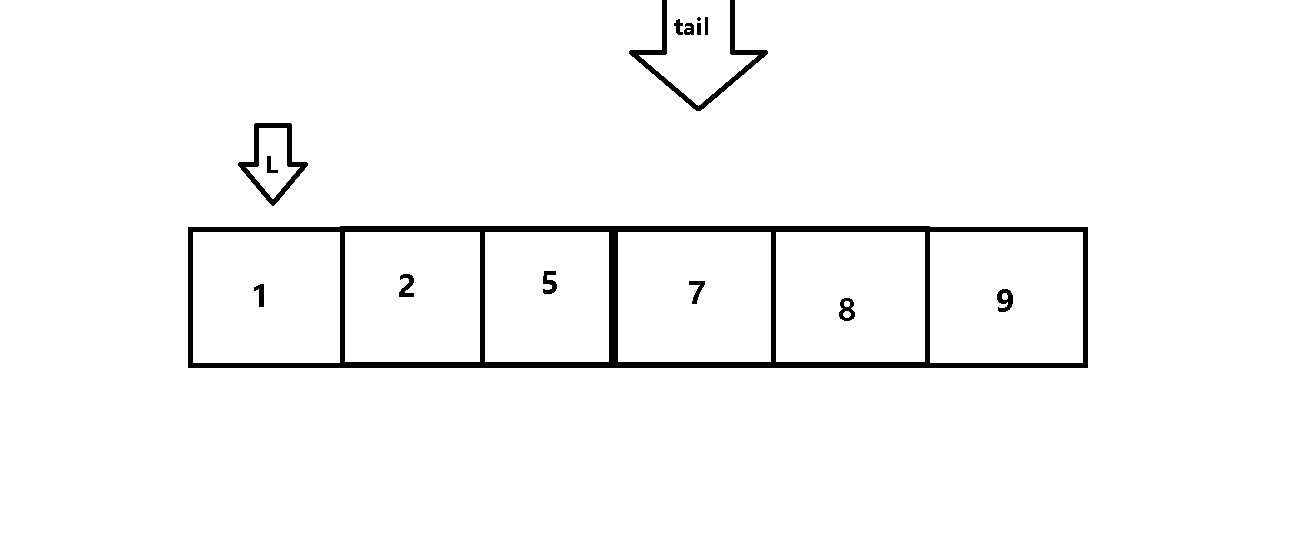
 代码如下：

//冒泡排序
void BubbleSort(int* pq, int k)
{
	int tail = k - 1;
	int L = 0;
	for (; tail>0; tail--)
	{
		for (L = 0; L < tail; L++)
		{
			if (pq[L] > pq[L + 1])
				swap(&pq[L], &pq[L + 1]);
		}
	}
}

感谢观看！！！