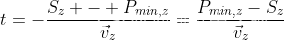张正友标定法--相机标定中的灭霸!
在上学期接触过calibration以后,下定决心要学一下张正友标定法的,然后没来的及学,寒假弥补一下。
参考博客:https://zhuanlan.zhihu.com/p/136827980

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面那3个矩阵相乘以后,得到单应矩阵H。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
就是说要想发挥出相机的高精度测量的能力,必须要进行标定。虽然相机在出厂的时候有标定的参数,但是这个出厂内参在实际使用过程中还是存在误差的,因此需要我们自行标定。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
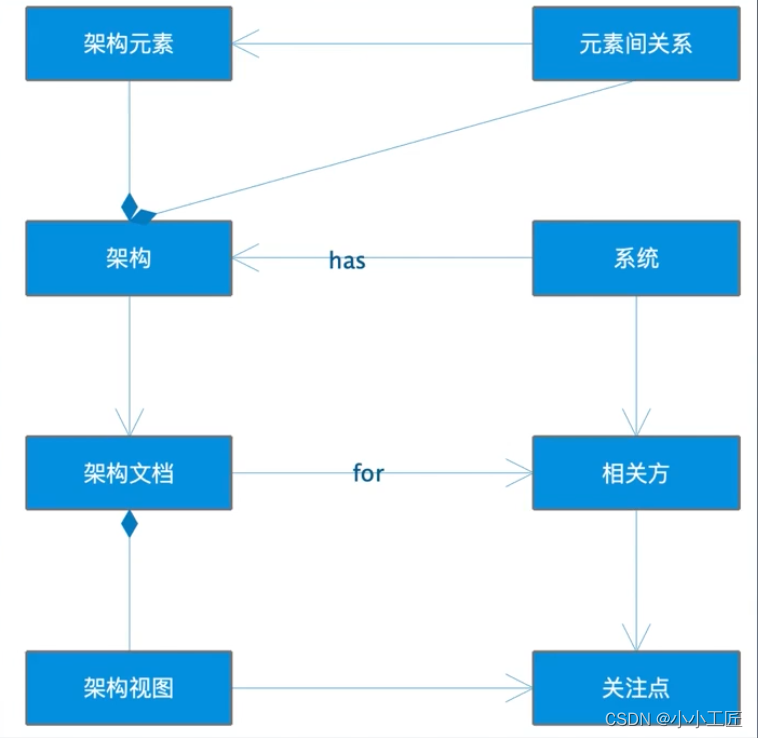
张氏标定法的地位,上图所示。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
张正友标定法的简明流程,就是通过自行打印的棋盘格,然后从不同角度获取照片。然后一顿计算,便得到了我们想要的内参。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
标定说白了还是在提高相机的精度。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这四个坐标系算是老朋友了,其中图像坐标系和像素坐标系是在一个平面上的,只不过两个坐标系的坐标原点不同,然后图像坐标系用xy表示,像素坐标系用uv表示。通常在写代码的时候我们一般默认uv就是像素坐标系上的点。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上图就是4个坐标系之间的关系。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
基元矩阵:就是绕着一个轴进行旋转的旋转矩阵,比如只绕着x轴旋转,那么这个旋转矩阵就叫做基元矩阵。(这个我第一次见)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
正交矩阵和旋转矩阵之间的关系,首先正交矩阵的行列式的绝对值为1,当正交矩阵的行列式为1时,此矩阵为旋转矩阵。如果正交矩阵的行列式为-1,那么这个矩阵称为镜面反射矩阵。
镜面反射变换:当xyz三维空间时,镜面反射变换就是 x=x’ y=y’ z=-z’ 就是沿着z轴对折了一下,当然这里是举个例子,也可能沿x轴或者y轴对折。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
对乘法封闭。
编辑切换为居中
添加图片注释,不超过 140 字(可选)
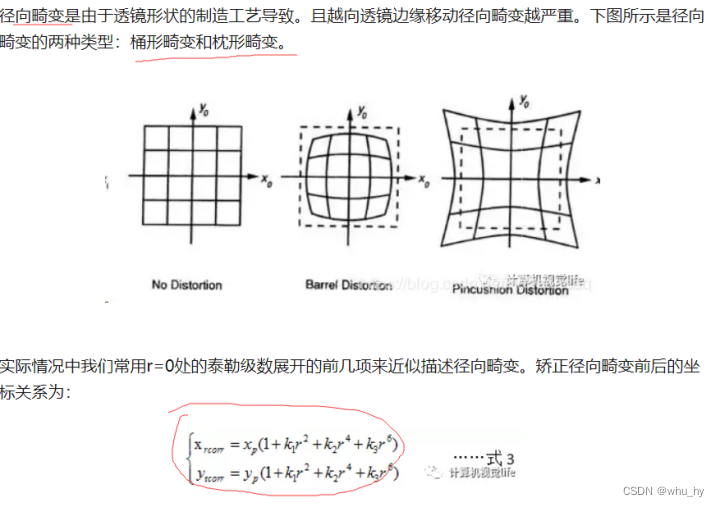
径向畸变的相关内容。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面的k1 k2 k3 p1 p2都是需要求解的畸变参数,这里的话畸变就是因为透镜的形状所引起的,但是这个畸变可以用数学的方式进行消除,所以没在透镜上面做文章。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这个图还是需要熟悉的。从世界坐标系到相机坐标系到图像坐标系再到像素坐标系。然后分别对应的矩阵,每个矩阵里面的含义都要知道。然后dx dy表示一个像素对应了多少米,这样就把米这个长度单位转换到了像素上面。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
单应矩阵的应用:

编辑切换为居中
添加图片注释,不超过 140 字(可选)
算是单应矩阵的应用,发现视角转变竟然是用的单应矩阵。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
单应矩阵,使用相机拍摄棋盘格,然后进行H的计算。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
张氏标定法就介绍到这里,对于这个方法的话如果不理解,也可以正确标出内参。使用matlab工具箱即可,集体操作过程可以自行百度搜索。