PCB结构和谐振（一）

实验研究

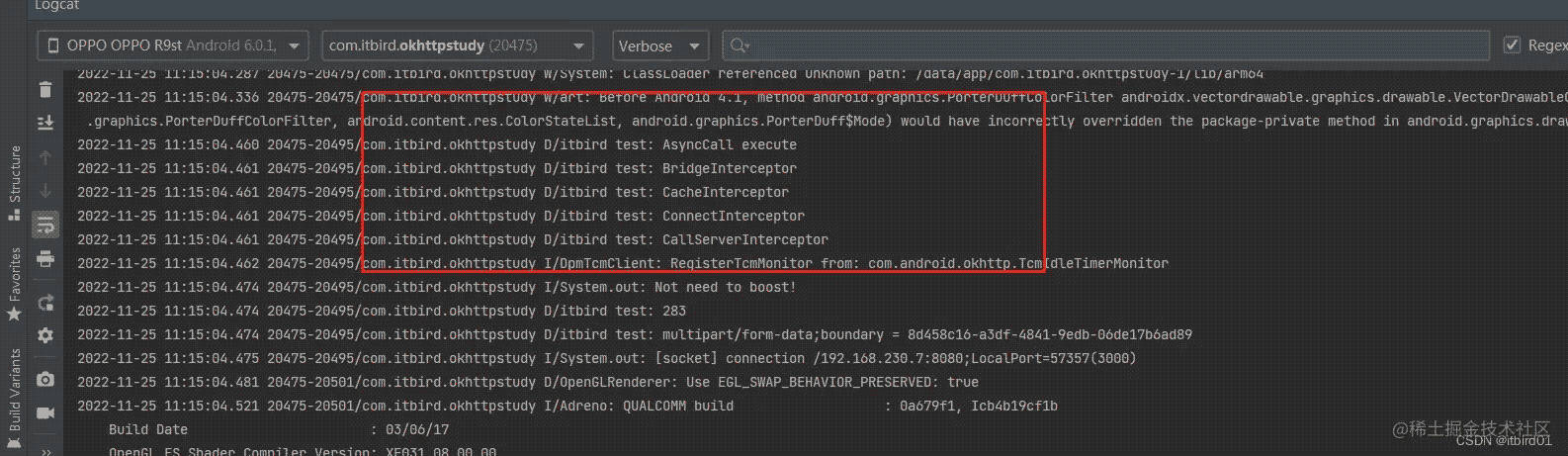
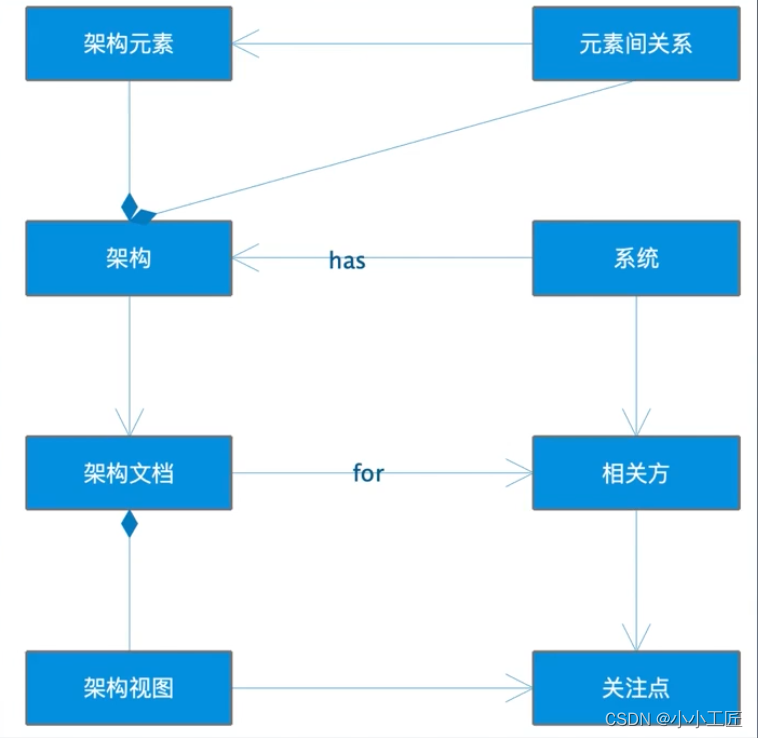
在此章节中，我们通过不同的测试研究了旋转角度/复杂层叠/走线pitch和layout设计等，所有的测试都是基于Intel Delta L 4.0规范。

旋转角度

单层结构是一个简单的层叠，所以首先通过测试单层结构研究谐振和旋转角度的关系。我们参考单层玻璃布来处理这些微带线作为单层结构。板材使用IT968G，下图是测试板的横截面示意图，两块测试板分别基于1078玻布和1080玻布，单张玻布厚度大约3mil，差分对走线长度10inch，线宽线距分别是5.8mil和6.2mil。

下图a和b展示了1078玻布不同旋转角度的SDD21曲线，图c和d展示了1080玻布不同旋转角度的SDD21曲线，角度指的是差分对和经向的夹角。1078 型布的相应谐振频率和强度如下表 2 所示，分别与公式 4、5 和 1 的周期长度（𝐿𝑤𝑎𝑟𝑝 𝑝𝑒𝑟𝑖𝑜𝑑, 𝐿𝑤𝑒𝑓𝑡 𝑝𝑒𝑟𝑖𝑜𝑑 ）、周期数（𝑁𝑤𝑎𝑟𝑝 𝑝𝑒𝑟𝑖𝑜𝑑, 𝑁𝑤𝑒𝑓𝑡 𝑝𝑒𝑟𝑖𝑜d）和预测频率（𝑓𝑤𝑎𝑟𝑝, 𝑓𝑤𝑒𝑓t）进行了比较。

结合上表和上图，发现所有的谐振都是由经向周期造成的，纬向的MS-glass玻璃束可以有效消除谐振。沿着纬向（MS-glass）走线效果很好。随着差分对走线方向和经向的夹角越来越大，经向周期引起的谐振频率也会越来越大，此外，两个与理论预测明显不同的现象值得我们注意:

现象1：

在图8的a和c中，对于每个旋转角度，在公式一预测的第一个谐振频率点下，仅看到了一个比较清楚的谐振，在高频并没有看到谐振，这个和谐振机制并不吻合。

现象2：

比较图a中旋转5°和旋转10°，随着旋转角度增加，在谐振频率附近往往会出现另一个显着的能量下降。

考虑到实际生产中存在加工公差，怀疑是玻璃束的自由分布导致了上述两个现象，这将在之后的章节中进行验证。

复杂叠层

高速差分对经常处于PCB的内层，为了研究内层的谐振，设置了三种情况，如下图所示，板材仍然是IT968G，所有玻纤布使用1078，差分对总长度10inch，线宽线距和厚度信息见下图。

下图展示了旋转10°情况下三种层叠的SDD21曲线，每种情况下都出现了两次谐振，一次较强一次较弱，两个谐振频率接近使用公式一预测的谐振频率。这个现象和上一节中单层结构的现象2比较类似，但更明显。除了上述玻璃束的随机分布外，实际旋转角度的不确定性也是一个促成因素。具体来说，对于内层结构，core侧的玻璃布由材料供应商处理，半固化片（PP）侧的玻璃布由PCB制造商处理，所以它们在层压过程中无法完美对齐。当我们将走线旋转一定角度时，它相对于PP和core的真实角度略有不同。

然后，我们计算了旋转 5 °和 10 °的三种情况下的谐振强度。每种情况的谐振强度的最大值、平均值和最小值如图11所示。一个明显的现象是，随着玻璃布数量的增加，谐振强度降低，这是因为玻璃布数量的增加削弱了Dk 分布的差异。

我们知道，当层压所用玻璃布的款式不同时，由于经向间距或Dk值的不同，对应的谐振频率也会不同。因此测量了如图12所示的不同玻璃布的测试板。这里使用的材料是 Meg 7(N)。这里的材料Dk是3.09。 1078型和1080型玻璃布的玻璃束间距差异可由表1得到。图 13 显示了这些测试板的 SDD21、SDD11、SDC11 和 SCD21 的大小。 SDD11、SCD11 和 SCD21 的幅度可以帮助我们确定 SDD21 幅度的谐振频率。获得了两个不同的谐振。借助方程式 1 和 4，我们确定了哪种类型的玻璃布引起了相应的谐振，如图 13 所示。

1080玻布的谐振要比1078玻布的谐振更小，两个原因导致了这种现象：

1.1080是3张玻布叠加，减小了Dk差异；

2.1078玻布只有1张，厚度太小，差分走线的电场更倾向于参考1078玻布侧的GND平面。

目前，我们发现无论层叠结构如何，引起谐振的主要周期仍然是由原始玻璃纤维间距引起的。在这里，我们给出我们的猜测：周期函数的叠加理论被用来解释这一点。叠加引起的新周期的长度是我们使用的所有玻璃间距的最小公倍数，不会小于原来的玻璃间距。这样，对于固定长度的差分对，原始玻璃间距引起的周期数将大于新周期数。

最后，我们可以得出结论，不同玻璃布的堆叠不会显着改变谐振频率，但会影响谐振强度。

差分对的pitch

图 14 比较了差分对的两个不同pitch的谐振强度。

将pitch从 12mil 增加到 14mil 不会显着改变谐振频率，但会降低谐振强度。

我们认为以下因素导致了这种现象：pitch更接近玻璃束间距值的差分对往往每个周期的skew更小。

两种周期性的layout设计

我们上面提到的测试车辆都是直线设计。这些测试车的横截面示意图与图7所示相同。考虑到实际PCB板尺寸的限制，我们在选择一些周期性布局设计时可能会引入新的周期。

图 15 显示了两种常见的设计，W 形线和蛇形线。它们的设计周期长度分别为1cm和0.6cm。两种设计都包括直段和弯段。直线段与弯曲段之间的夹角为10度或80度，对应的谐振频率为30GHz左右。差分对的间距值为12mil。所以我们只测量高达 20GHz 的 S 参数，以研究设计周期引起的谐振。

图 16 显示了两种导线设计的 SDD21 的大小。每个设计都显示出许多谐振，这与这些旋转案例非常不同。这是因为设计周期是统一的，与玻璃束引起的这些周期不同。通过计算表3中谐振对应的周期长度，可知谐振频率与设计周期的关系。

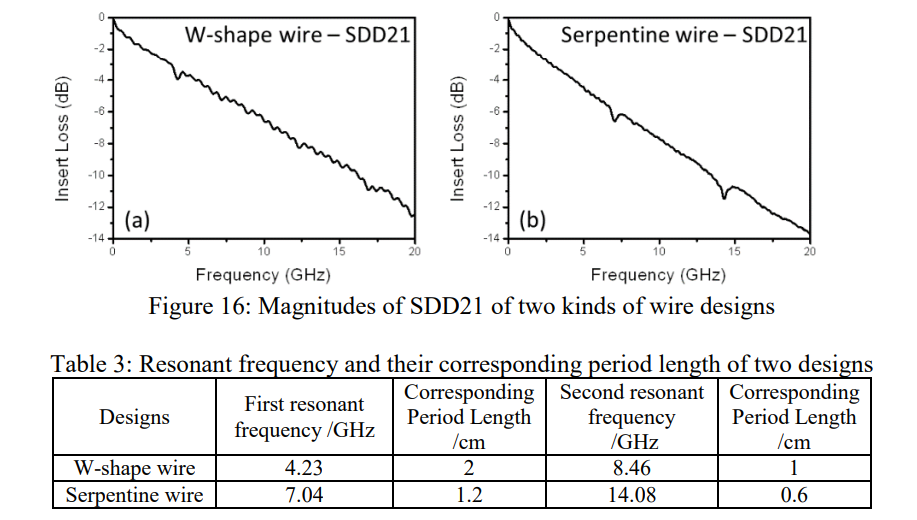
表 3 仅显示了每个设计的前两个谐振频率。我们认为其他较高的谐振频率是前两个谐振频率的奇数倍。为什么我们找到每个设计的两个对应的周期长度？我们将详细讨论两个不同周期的原因。

以下是两种设计中的主要不连续点及其对应的周期：

不连续性（1）：差分信号通过弯段时，由于P、N走线长度不同，实际截面积会比直段大，导致弯段阻抗略低比直线段，从而形成阻抗不连续模型，其周期长度恰好是上述设计周期长度。

不连续性（2）：考虑编织结构，图15中点1和点3形成的参考线恰好平行于经线，因此点1和点3的介电常数比较接近。对于点 2 和点 4 也是如此。但是点 1 和点 2 可能具有不同的 Dk 值，因为经向的 Dk 存在很大的不均匀性。所以点 1 到点 2 到点 3 也形成了另一个阻抗不连续模型，其周期长度恰好是设计周期长度的两倍。

不连续性（3）：当差分信号通过弯曲段时，由于P和N走线的长度不同，会出现skew。 P 和 N走线之间的 Dk 差异也会导致这种skew。参考上述skew不连续模型，周期为点1到点2再到点3。

在三个不连续性中，只有不连续性（1）完全来自导线设计本身。不连续性 (2) 和 (3) 来自线材设计和编织结构。线材设计和编织结构之间的关系将在后面进行讨论。