大家好，又和大家见面啦！今天我们一起去看一下二叉树的前序中序后序的遍历，相信这个对大家来说是信手拈来，但是，今天我们并不是使用常见的递归方式来解题，我们采用迭代方式解答。我们先看第一道前序遍历 

1、前序遍历

二叉树的前序遍历

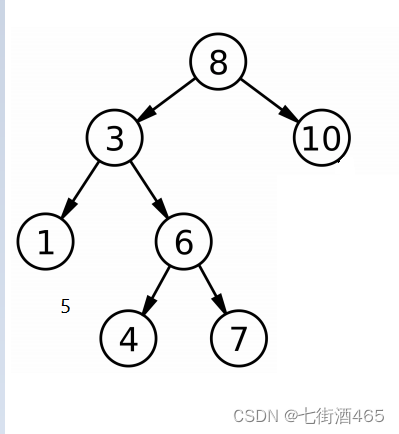
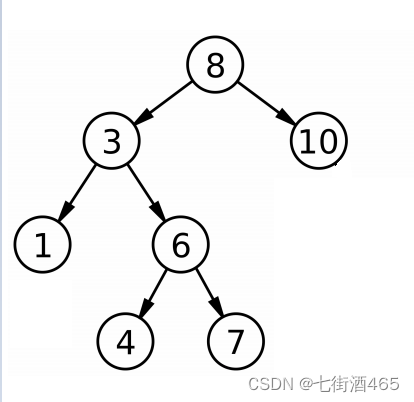
前序遍历是先将二叉树的根节点遍历，再遍历左子树、右子树。我们做这道题的思想是把二叉树划分为两部分，一是左路节点，二是左路节点的右子树。什么是左路节点，如上图的二叉树来说，

这就算以8为根节点的二叉树的左路节点，也就是以8为根节点，它的左孩子的左孩子的左孩子......这一条路径。我们先让左路节点入栈，因为是前序遍历，所以我们入栈的同时，遍历当前结点的val，当左路结点都入栈完，那么当前节点一定是没有左子树的，我们让这个结点出栈，这个时候我们处理当前结点的右子树，右子树同样进行先让左路节点入栈.....循环做此操作，直到右子树也会空，然后将这个结点的所有左右子树我们都访问完成，我们已经pop掉这个时候，只需要处理新的栈顶元素就可以啦。

话不多说，思路就是这个样子，下面把代码写出来让大家看看。

定义一个cur从根节点开始，然后定义一个栈存储左路结点，一个vector存储左路节点的数据。

vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur=root;//cur从根节点开始

        while(cur)
        {
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);//左路结点入栈
                cur=cur->left;
            }
            //处理栈内的右子树
            TreeNode* top=st.top();
            st.pop();
            cur=top->right;//处理左路节点的右子树

        }
        return v;
    }

代码写起来很简单，但是我们会发现这个提交是过不了的，为什么呢？大家看，我们在把1的右节点赋给cur去处理1的右子树时，结点1是没有右结点的，这个时候cur为空，上面这个大循环就进不去，而这个时候，我们其它的左路节点都还在栈里面没有处理，所以，外面这个大循环的判断条件是不正确的。应该改成

while(cur||!st.empty())

当栈不为空的时候，我们也要处理。 然后我们再运行，就可以通过了。

2、中序遍历

二叉树的中序遍历

我们还是拿这棵树来看，其实中序和前序思路是完全一样，只不过前序的遍历顺序是根左右，我们左路结点入栈的时候就可以直接访问其val，但是中序遍历的顺序是左根右，所以我们写中序的时候应该把访问val的顺序调到结点出栈的时候访问就可啦。

下面我们开始实现

vector<int> inorderTraversal(TreeNode* root) {
    stack<TreeNode*> st;
    vector<int> v;
    TreeNode* cur=root;
    while(cur||!st.empty())
    {
        while(cur)//左路结点进栈
        {
            st.push(cur);
            cur=cur->left;
        }
        TreeNode* top=st.top();
        v.push_back(top->val);
        st.pop();
        cur=top->right;//处理当前结点的右子树
    }
    return v;
    }

3、后序遍历

二叉树的后序遍历

后序遍历的遍历顺序是左右根，我们只有把左右结点全部访问完成才能访问根节点的数据，或者左右节点为空才能直接访问根节点的数据。左节点我们在左路子树入栈的时候就算是访问，但是右节点怎么解决呢？

所以说，我们这里需要解决一下，怎么才能知道右节点已经访问过了。我们以这里的结点6为例，要访问结点6的val,首先，我们把8，3，1入栈，结点1没有右子树，可以直接获取它的val,出栈后，栈顶元素是3，3有右子树，需要先处理它的右树，，然后6，4入栈，这时栈顶结点为4，4没有右树，直接获取它的val，此时栈顶元素为6，6他有右树，需要先处理他的右树，此时结点7入栈，这个时候7没有右树，直接获取它的val，这个时候结点6的左右树都访问完毕，可以访问6的val了，但是我们怎么判断结点6的左右树都已经访问完毕了呢？结点6上一次访问的结点是7，我们只需要判断，6结点的上一次访问的结点是不是7就可以了。

我们可以定义一个结点prev,每访问完一个栈顶元素，我们就把top赋给prev，表示上一个访问结点，我们只需要判断top->right==prev，即我们已经访问过top->right这个结点就行了，这样我们可以直接获取栈顶的val值。

因此，只有在当前结点的右树为空，或者当前结点的右结点是我们上一次访问的结点，我们就可以获取它的val值。

下面我们开始写代码

vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur=root;
        TreeNode* prev=nullptr;
        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode* top=st.top();
            //分情况讨论，如果当前这个结点的右子树为空，或者当前结点的右子树是我们上次访问的结点；表示我们已经访问过它的子树，就可以直接获取当前结点的val
            if(top->right==nullptr||top->right==prev)
            {
                st.pop();
                v.push_back(top->val);
                prev=top;
            }
            //否者，访问这个结点的右树
            else{
                cur=top->right;
            }
        }
        return v;

到这里，二叉树的前序中序后序三个非递归方式就讲解完毕啦。我们下次再见呀