概率是随机的基础,在【概率论(概要)】这个部分中仅记录学习随机过程及应用的基本定义和结果。
 前言
前言
首先,概率论研究的基础是概率空间。概率空间由一个样本空间和一个概率测度组成,样本空间包含了所有可能的结果, 而概率测度则描述了每个结果发生的可能性大小。研究者通过定义适当的概率测度,可以更准确地描述各种随机现象的发生概率。
一、概率空间 (Ω,F,P)
Sample space 样本空间:随机试验的所有可能结果构成的集合称为样本空间,记为 Ω。(注:每个结果需要互斥,所有可能结果必须被穷举)
Set of events 事件集合,是Ω的一些子集构成的集合,记为 F,并且它需要满足以下三点特性(也就是必须是δ-field)
Probability measure 概率测度(或概率),描述一次随机试验中被包含在F 中的所有事件的可能性,记为P。
- 样本点(Sample point):随机试验E的每一个最简单的试验结果,记为
。
- 样本空间( Sample space):全体样本点构成的集合,称为样本空间Ω
- 事件(Event):
- 样本空间的子集组成的集类F,称为随机事件体(域)。
- 随机事件体F的任意元素A称为随机事件。
- 样本空间o和F的二元体(Ω,F)称为可测空间。
- 概率(Probability):每个事件一个可能性的度量值。
1、随机试验
定义:如果一个实验E,满足下列条件:
- 在相同的条件下可以重复进行;
- 每次试验的结果不止一个,并且能事先明确试验的所有结果;
- 一次试验结束之前,不能确定哪一个结果会出现。
称此试验为随机试验。 随机试验(Experiment):结果无法预先确定的试验。 随机试验的结果,称为事件。
2、集论初步
- 在概率论中,事件和事件的集合起主要作用。
- 事件的数学理论和集论有密切关系,用集论描述随机过程的事件。
把为了某种目的而研究的对象全体称为集合,简称为集。有某些特定性质的对象的全体,每一个属于这种集的对象,称为集元素。集合用大写字母A、B、C、…表示,元素用小写字母a、b、c、e、w、…表示,一些集组成的集叫类,我们用草写字母表示。
- 不包含任何元素的集合称为空集
- 包含所研究问题的全体对象,即:包含所考虑的所有集的所有元素的“最大”集合,称为空间Ω
集合的运算:

3、样本空间、随机事件体
随机试验E的每一个最简单的试验结果,称为样本点,记为。全体样本点构成的集合,称为样本空间,记为Ω。

集合论和概率论的专业术语对应关系如下表所示:

4、概率与概率空间

概率的性质与基本公式:

(6)连续性

5、条件概率

6、乘法公式事件的独立性
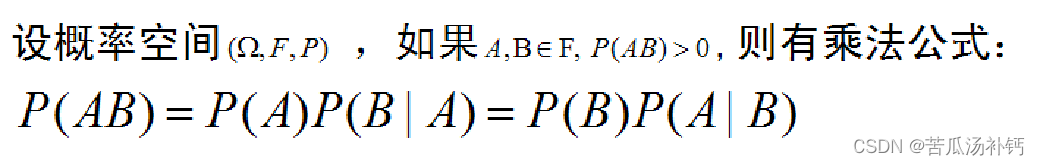
随机事件的独立性:

7、全概率公式与贝叶斯公式

二、随机变量及其分布
1、随机变量

2、分布函数

3、离散型随机变量及其分布律

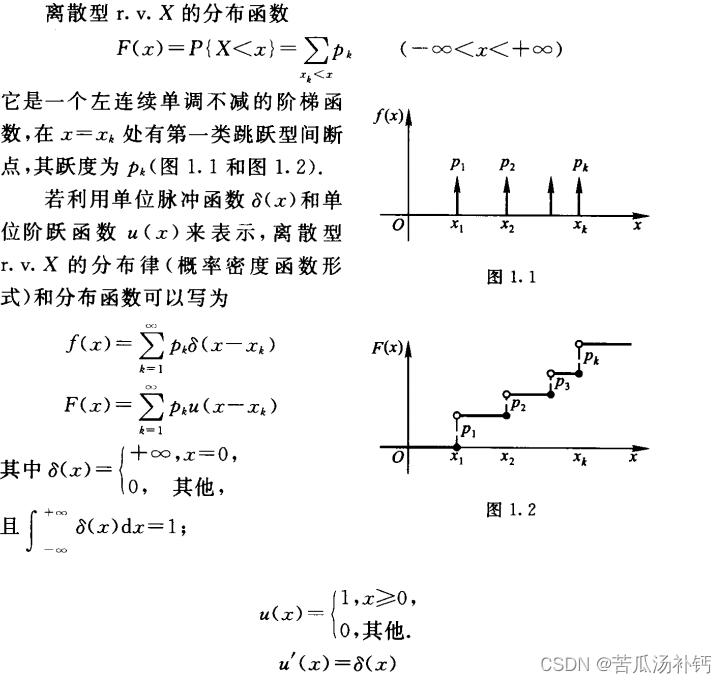
4、连续型随机变量

5、常见的随机变量及其分布
两点分布
两点分布(也称为伯努利分布)是概率论中一种离散概率分布,描述了一个随机变量取两个可能值之一的情况。这两个可能的取值通常被标记为0和1,或者成功和失败。该分布得名的原因是它只涉及到两个点。
两点分布的概率质量函数(PMF)可以表示为:

其中,p 是成功的概率,1−p 是失败的概率。这样的分布通常用于描述一次伯努利试验的结果,其中只有两个可能的结果。
两点分布的期望值(均值)和方差分别为:
- E(X)=p
- Var(X)=p(1−p)
其中,X 是随机变量,p 是成功的概率。
二项分布
二项分布(Binomial Distribution)是概率论中一种离散概率分布,描述了在进行一系列独立的伯努利试验中成功的次数。每次试验只有两种可能的结果,通常称为成功(success)和失败(failure)。
假设进行了 n 次独立的伯努利试验,每次试验成功的概率为 p,失败的概率为 1−p。随机变量 �X 表示成功的次数,则 X 的概率质量函数(Probability Mass Function,PMF)为:
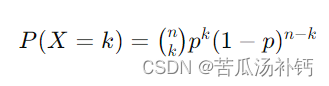
其中,(kn) 表示组合数,即从 n 次试验中选择 k 次成功的组合数。
二项分布的期望值(均值)和方差分别为:
E(X)=np
Var(X)=np(1−p)
这表明在进行多次独立的伯努利试验时,成功的次数的期望值等于每次试验成功的概率乘以试验次数,方差等于期望值乘以失败的概率。
二项分布在概率论和统计学中广泛应用,特别是在描述二元事件的发生次数的情况下,如硬币抛掷、医学研究中的治疗效果、制造业的质检等。
均匀分布
在二维均匀分布中,随机变量(X,Y) 在一个矩形区域内均匀分布。概率密度函数为:

其中,区域的面积决定了概率密度的大小。
均匀分布具有简单且直观的性质,适用于许多实际问题的建模,例如在一定范围内的随机实验或随机变量。均匀分布在统计学、概率论、模拟和随机过程等领域中经常被使用。
高斯分布
高斯分布,也被称为正态分布(Normal Distribution),是概率论和统计学中最为重要的分布之一。它具有许多重要的性质,对于自然界中的许多现象和实验结果都有很好的描述。
高斯分布的概率密度函数(Probability Density Function,PDF)为:

其中,x 是随机变量的取值,μ 是均值(期望值),σ 是标准差。这个分布的图像呈钟形,关于均值对称。
高斯分布的期望值(均值)为 μ,方差为 2σ2。标准差 σ 控制了曲线的宽度,曲线越宽表示数据越分散。
高斯分布在自然界中的许多现象中都能够找到,比如测量误差、身高分布、温度分布等。中心极限定理表明,当独立随机变量的和足够多时,它们的分布趋向于高斯分布。这使得高斯分布在统计学和概率论中被广泛应用,特别是在推断统计、假设检验和机器学习等领域。
三、随机变量的数字特征
1、数字期望

2、方差

3、矩、协方差


4、随机变量数字特征的性质
四、条件数学期望
五、特征函数
1、定义与性质
一般而言,对于随机变量X的分布,大家习惯用概率密度函数来描述,虽然概率密度函数理解起来很直观,但是确实随机变量的分布还有另外的描述方式,比如特征函数。
- 特征函数的本质是概率密度函数的泰勒展开
- 每一个级数表示原始概率密度函数的一个特征
- 如果两个分布的所有特征都相同,那我们就认为这是两个相同的分布
- 矩是描述概率分布的重要特征,期望、方差等概念都是矩的特殊形态
随机变量X的特征函数:
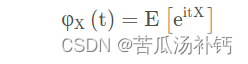
其中,i是虚数单位,t是任意实数,E[⋅]表示期望。
性质:
-
存在性: 对于任何随机变量X,它的特征函数总是存在的。
-
唯一性: 不同的随机变量可能具有相同的特征函数,但如果两个随机变量的特征函数在某个范围内相等,则它们在分布上相同。
-
特征函数与分布的关系: 如果两个随机变量具有相同的特征函数,则它们具有相同的分布。
-
特征函数的对称性: 如果X是一个实随机变量,其特征函数为φ(t),则对于任意实数t,有 ϕ(−t)=ϕ(t),其中ϕ(t)表示φ(t)的共轭复数。
-
特征函数的加法性: 如果X和Y是相互独立的随机变量,它们的特征函数分别为φX(t)和φY(t),那么它们的和Z = X + Y 的特征函数为 ϕZ(t)=ϕX(t)⋅ϕY(t)。
-
中心极限定理: 如果X1, X2, ..., Xn是独立同分布的随机变量,具有相同的期望μ和方差σ^2,则它们的和标准化后的特征函数在n趋于无穷大时趋近于正态分布的特征函数。
特征函数在概率论和统计学中有广泛的应用,它提供了一种便捷的方式来研究随机变量的性质和相互关系。
针对概率密度函数为f ( x )的连续随机变量X,特征函数写作:
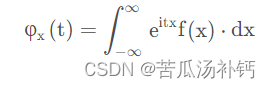
2、多维随机变量的特征函数

-
存在性: 对于任何多维随机变量 X,其特征函数总是存在的。
-
唯一性: 不同的随机变量可能具有相同的特征函数,但如果两个随机变量的特征函数在某个范围内相等,则它们在分布上相同。
-
特征函数与分布的关系: 如果两个多维随机变量具有相同的特征函数,则它们具有相同的分布。
-
特征函数的对称性: 如果多维随机变量 X 的特征函数为ϕX(t),则对于任意实数向量 t,有 ϕX(−t)=ϕX(t),其中 ϕX(t) 表示特征函数的共轭复数。
-
多维随机变量的独立性: 如果多维随机变量 X 和 Y 是相互独立的,它们的特征函数分别为 ϕX(t) 和 ϕY(t),那么它们的组合 Z=X+Y 的特征函数为 ϕZ(t)=ϕX(t)⋅ϕY(t)。
六、收敛性与极限定理
1、收敛性

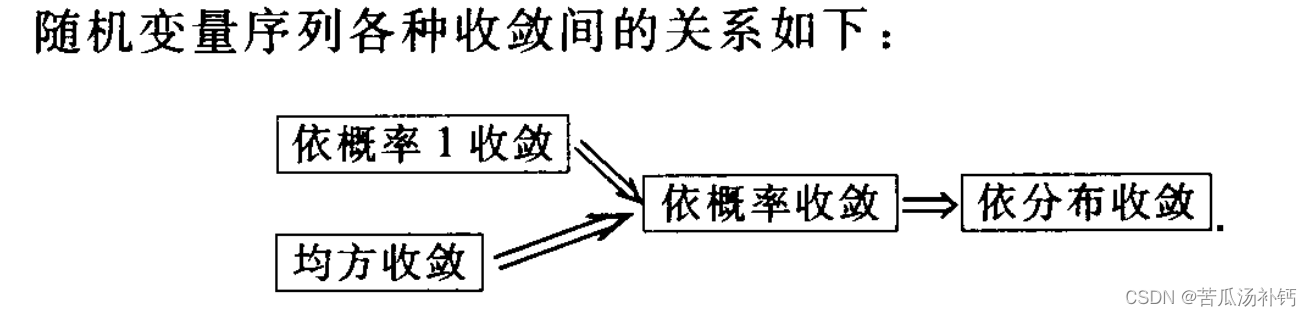
2、大数定理

3、中心极限定理

总结
以上就是今天要讲的内容,仅仅简单介绍了一些概率论的基本概念。