一、概念介绍

输出比较：

比较电路输入的CNT、CCR大小关系 ，在通道引脚输出高低电平

二、频率知识、测量方法补充 

N/fc得到标准频率的时长，也就是待测频率的周期

测频法代码实现：修改对射式红外传感器计次（上升沿计次）、定时器外部时钟（1s中断） 

测频法：定时器中断，并记录捕获次数；测周法：捕获中断，并记录定时器次数。

三、输入捕获电路分析如何实现测周法：

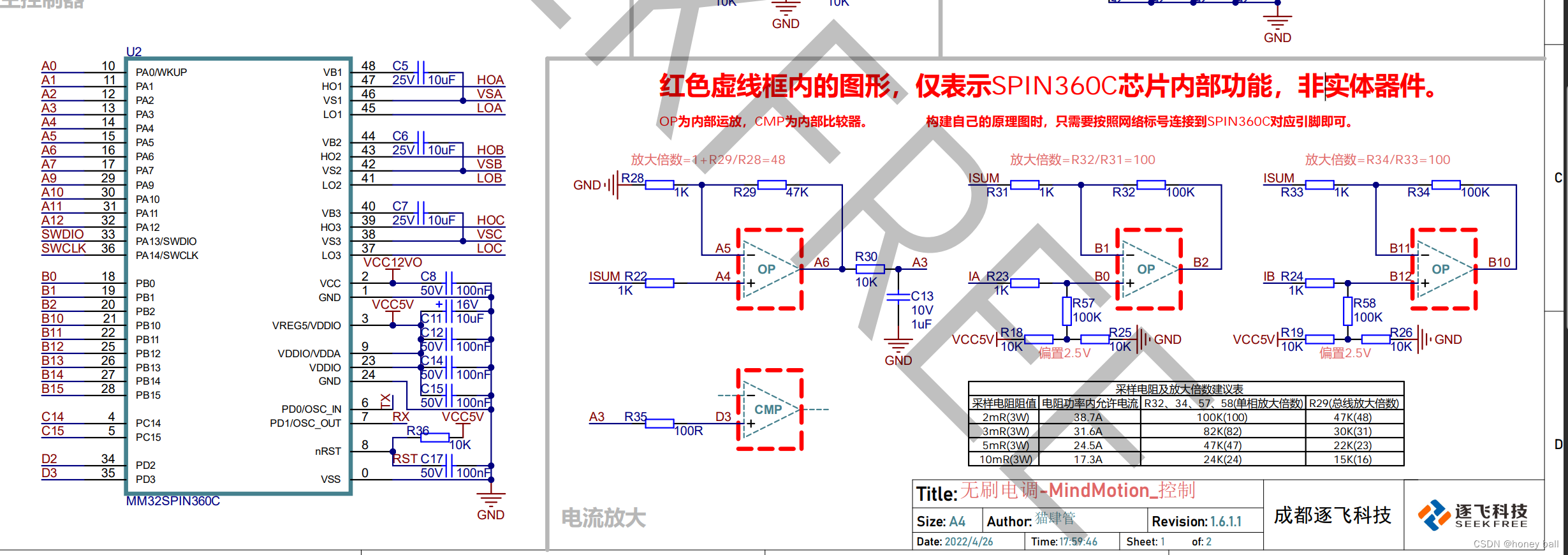
异或门其实还是为三相无刷电机服务，三个霍尔传感器检测转子位置，根据转子位置进行换相，在前三个通道接上霍尔传感器，这个定时器就作为无刷电机的接口定时器，去驱动换相电路工作

输入滤波器：避免毛刺

3.1设计成交叉状的目的：

TI1FP1(TI1 Filter Polarity 1) -->IC1<--TI2FP1

TI1FP2-->IC2<--TI2FP2

（1）灵活切换后续捕获电路输入 CH1变成CH2   即一个通道切换两个引脚

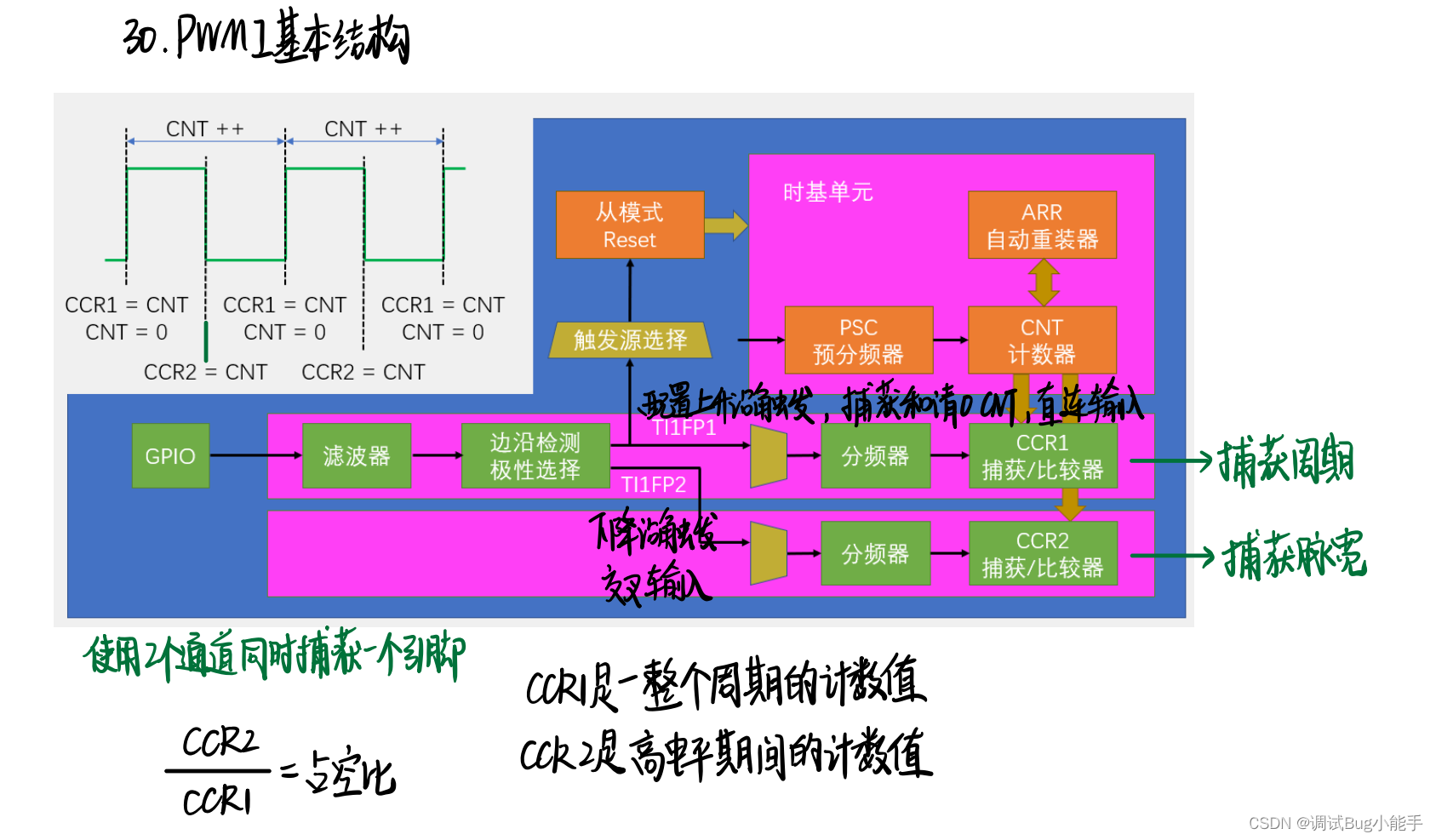
（2）把一个引脚的输入，同时映射到两个捕获单元（PWMI模式经典结构） 即两个捕获单元捕获一个引脚

举例：

第一个捕获通道？TI1FP1上升沿触发，用来捕获周期

第二个捕获通道TI1FP2下降沿触发，用来捕获占空比

两个通道同时对一个引脚进行捕获

3.2预分频器（测周法实现）&捕获中断

*设置上升沿触发，分频后的触发信号每来一次，CNT就会向CCR转运一次，又因为CNT是内部的标准时钟驱动的，CNT数值就可以记录两个上升沿之间的时间间隔，也就是周期，取倒数得到频率

上升沿用于触发输入捕获，CNT用于计数计时

捕获中断：同时产生捕获事件，这个事件在状态寄存器置标志位，同时也可以产生中断

3.3应用场景：超声波模块检测电路

3.4细节问题

每次捕获后，把CNT清零，这样下次上升沿再捕获，取出的CNT 才是两个上升沿的时间间隔

用主从触发模式自动完成

四、电路执行细节

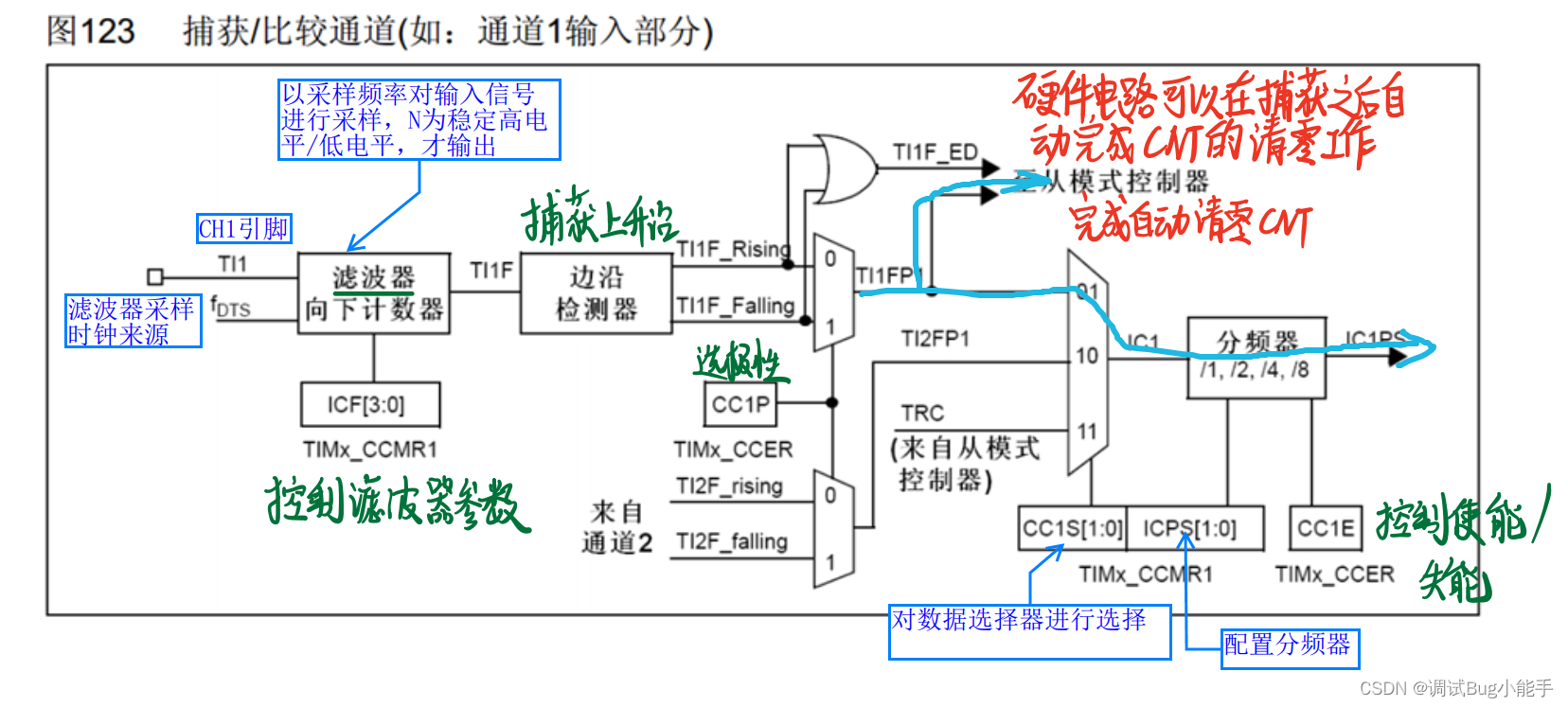
 注意：

CNT的值是有上限的（65535=ARRmax），若信号频率太低，CNT计数值会溢出

 从模式的触发源选择：TI1FP1 TI2FP2没有3,4 想用从模式自动清零CNT,只能用通道1和通道2，对于通道3和通道4只能开启捕获中断，手动清零

-->Q:能否外部中断？ AS:概念不清，外部中断那是CPU了啊，这里是硬件映射主模式，然后配置从模式

 也可以捕获第二个引脚：TI2FP1 TI2FP2