Java解决下降路径最小和

01 题目

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

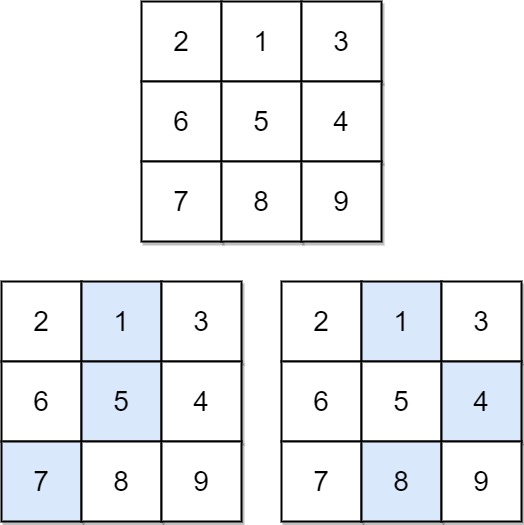
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

02 知识点

• 双重循环
• 二维数组
• 动态规划

03 我的题解思路

public class shuzu02 {
	public static void main(String[] args) {
//		测试数据
		int[][]	matrix = {
				{2,1,3},
				{6,5,4},
				{7,8,9}
		       	        		  };
		
		System.out.println(minFallingPathSum(matrix));
	}
	public static int minFallingPathSum(int[][] matrix) {
//		获取行数和列数
		int row=matrix.length;
		int col=matrix[0].length;
//		用二数数组来实现dp（动态规划）
//		动态规划，我的理解是用算法记录计算出结果的每一个阶段的过程值
		int[][] nums=new int[row][col];
		for (int i = 0; i < row; i++) {
//			每一行循环
			for (int j = 0; j <col; j++) {
//				每一列循环,当为第一行的时候,赋值并直接结束本次列循环
				if (i==0) {
					nums[0][j]+=matrix[i][j];
					continue;
				}
//				从第二行开始,到达第二行每一格都存在最优解,最优解(nums[i][j])=原本值(matrix[i][j])＋上一行相邻格中最小值
//				循环找到上一行相邻格中最小值
				int min=Integer.MAX_VALUE;
				for (int j2 = j-1; j2 <j+2; j2++) {
//					为了放在数组越界，要去除临界值
					if (j2<0||j2>col-1) {
						continue;
					}
					min=Math.min(min, nums[i-1][j2]);
				}
				nums[i][j]=matrix[i][j]+min;	
			}
		}
//		最后再从结果表最后一行中取出最小路径和
		int min=Integer.MAX_VALUE;
		for (int i = 0; i < col; i++) {
			min=Math.min(min, nums[row-1][i]);
		}
		return min;
    }
}