政安晨：【示例演绎】【Python】【Numpy数据处理】快速入门（四）—— 函数方法

news2024/11/24 3:02:48

准备工作


这是Numpy数据处理的示例演绎系列文章的第四篇，我的前三篇文章为：

政安晨：【示例演绎】【Python】【Numpy数据处理】快速入门（一）icon-default.png?t=N7T8https://blog.csdn.net/snowdenkeke/article/details/136125773政安晨：【示例演绎】【Python】【Numpy数据处理】快速入门（二）icon-default.png?t=N7T8https://blog.csdn.net/snowdenkeke/article/details/136127590政安晨：【示例演绎】【Python】【Numpy数据处理】快速入门（三）—— 数组的操作icon-default.png?t=N7T8https://blog.csdn.net/snowdenkeke/article/details/136130381小伙伴们准备好环境后，咱们这就开始。

概述

NumPy提供了许多常用函数，用于数值计算、统计、线性代数等领域，以下是一些常用的NumPy函数的简单介绍：

  1. np.array()：用于创建一个数组。

  2. np.linspace()：返回在指定间隔内的等间隔数字。

  3. np.zeros()：返回一个全零的数组。

  4. np.ones()：返回一个全一的数组。

  5. np.eye()：返回一个单位矩阵。

  6. np.random.rand()：返回一个指定形状的随机数组。

  7. np.arange()：返回一个指定间隔和步长的数组。

  8. np.reshape()：用于改变数组的形状。

  9. np.transpose()：用于转置数组。

  10. np.dot()：用于两个数组的点积运算。

  11. np.sum()：计算数组元素的和。

  12. np.mean()：计算数组元素的平均值。

  13. np.max()：返回数组中的最大值。

  14. np.min()：返回数组中的最小值。

  15. np.std()：计算数组元素的标准差。

  16. np.var()：计算数组元素的方差。

这只是一些常用的NumPy函数的简要介绍，NumPy还提供了很多其他的函数和方法，这些函数其实是数组对象内置的方法，可以根据具体需求来选择使用，咱们介绍和函数相关的几个概念，并对部分常用函数做示例性讲解，简单介绍。

常量

说起常量，我们首先会想到圆周率、自然常数、欧拉常数等。的确，NumPy的常量包括np.pi（圆周率）、np.e（自然常数）、np.euler_gamma（欧拉常数），此外还包括np.nan（非数字）和np.inf（无穷大）这两个特殊值，NumPy的特殊值还有正负无穷大、正负零等，但因为很少用到，这里就不进行重点介绍。

NumPy有两个很有趣的特殊值：np.nan和np.inf。

nan是Not a Number的简写，意为非数字；inf是infinity的简写，意为无穷大。其代码如下：

a = np.array([1, 2, np.nan, np.inf])
a.dtype

a[0] = np.nan
a[1] = np.inf
a

# 两个np.nan不相等
a[0] == a[2] 

# 两个np.inf则相等
a[1] == a[3] 

# 判断一个数组元素是否是np.nan
np.isnan(a[0]) 

# 判断一个数组元素是否是np.inf
np.isinf(a[1])

以下代码演示了在数组相邻的两个元素之间插入它们的算术平均值，尽管数组元素包含np.nan，但这不影响数值计算：

a = np.array([9, 3, np.nan, 5, 3])
a = np.repeat(a,2)[:-1]
a[1::2] += (a[2::2]-a[1::2])/2
a

演绎如下：

命名空间

在Numpy中，实现同样的功能，一个函数却有两种写法；有时以为某个函数可以有两种写法，但用起来却会出错。归纳起来，这些困惑有以下三种类型：

（1）都是求和、求极值，下面这两种写法有什么区别吗？

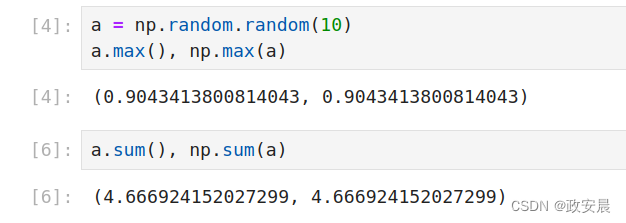
a = np.random.random(10)
a.max(), np.max(a)

a.sum(), np.sum(a)

演绎：

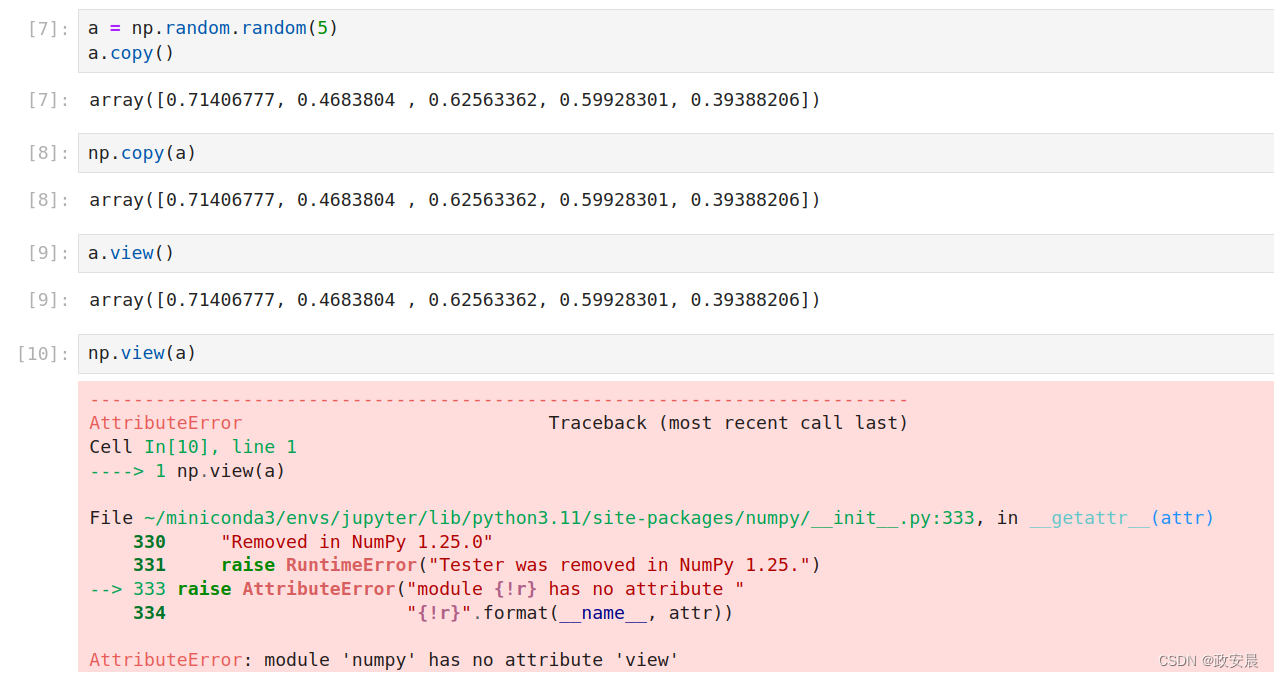
（2）同样是复制，为什么深复制copy( )两种写法都行，而浅复制view( )则只有数组的方法？

a = np.random.random(5)
a.copy()

np.copy(a)

a.view()

# 这种会报错
np.view(a)

演绎：

（3）为什么where( )不能作为数组ndarray的函数，必须作为NumPy的函数？

np.where(a>0.5)

a.where(a>0.5)

演绎：

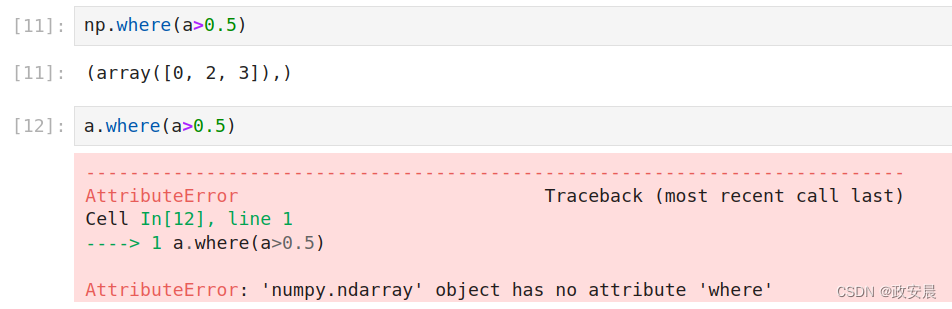
以上这些差异取决于函数在不同的命名空间是否有映射，数组的大部分函数在顶层命名空间有映射，因此可以有两种写法，但数组的一小部分函数没有映射到顶层命名空间，所以只能有一种写法。而顶层命名空间的大部分函数，也都只有一种写法。

下表所示的是常用函数和命名空间的关系：

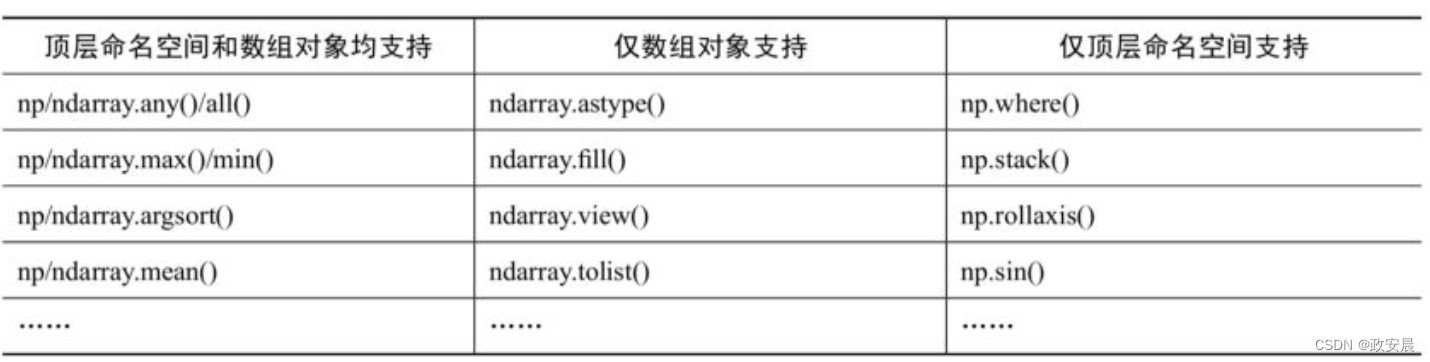
数学函数

如果不熟悉NumPy，Python程序员一般都会选择使用math模块来解决数学问题。

但实际上NumPy的数学函数比math模块更加方便，而且NumPy的数学函数可以广播到数组的每一个元素上，也就是说，如果用np.sqrt( )对数组arr开方，返回的是数组arr中每个元素的平方根组成的新数组。

下面把NumPy和math模块的数学函数罗列在一个表格中，分成了数学常数、舍入函数、快速转换函数、幂指数对数函数和三角函数这5类：

（其他如求和、求差、求积的函数被归类到下一小节的统计函数中。）

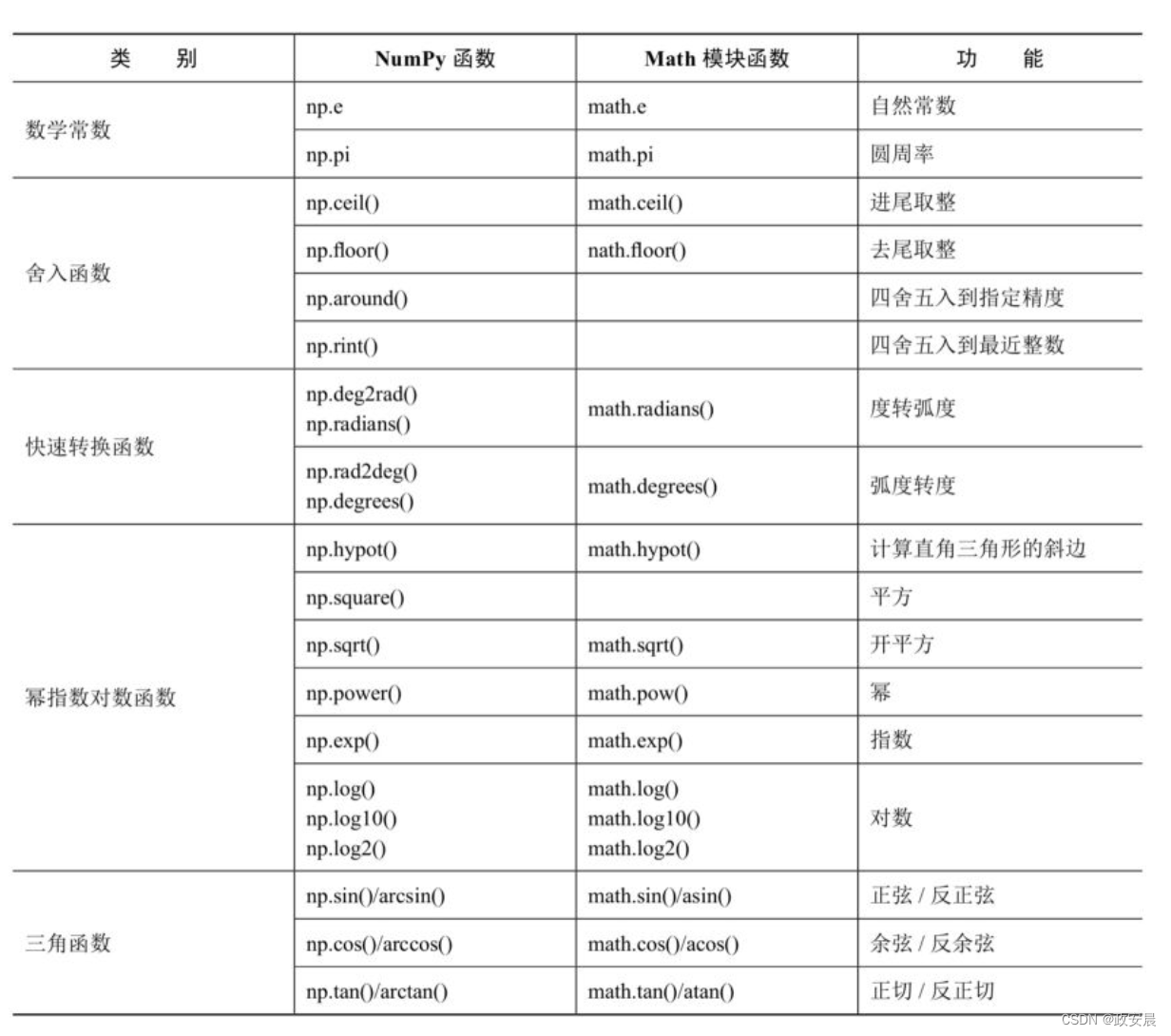
下面的代码演示的是一些常用数学函数：

import numpy as np
import math

# 两个模块的自然常数相等
math.e == np.e 

# 两个模块的圆周率相等
math.pi == np.pi 

np.ceil(5.3)
np.ceil(-5.3)
np.floor(5.8)
np.floor(-5.8)
np.around(5.87, 1)
np.rint(5.87)
np.degrees(np.pi/2)
np.radians(180)

# 求平面上任意两点的距离
np.hypot(3,4) 

np.power(3,1/2)

np.log2(1024)

np.exp(1)

#正弦、余弦函数的周期是2π
np.sin(np.radians(30)) 

np.sin(np.radians(150))

# 反正弦、反余弦函数的周期则是π
np.degrees(np.arcsin(0.5))

小伙伴们可以自己尝试一下。

统计函数

NumPy的统计函数有很多，并且很多函数还同时提供了忽略nan（缺值或无效值）的形式。常用的统计函数大致上可以分成查找特殊值、求和差积、均值和方差以及相关系数这4类，详细说明如下表所示：

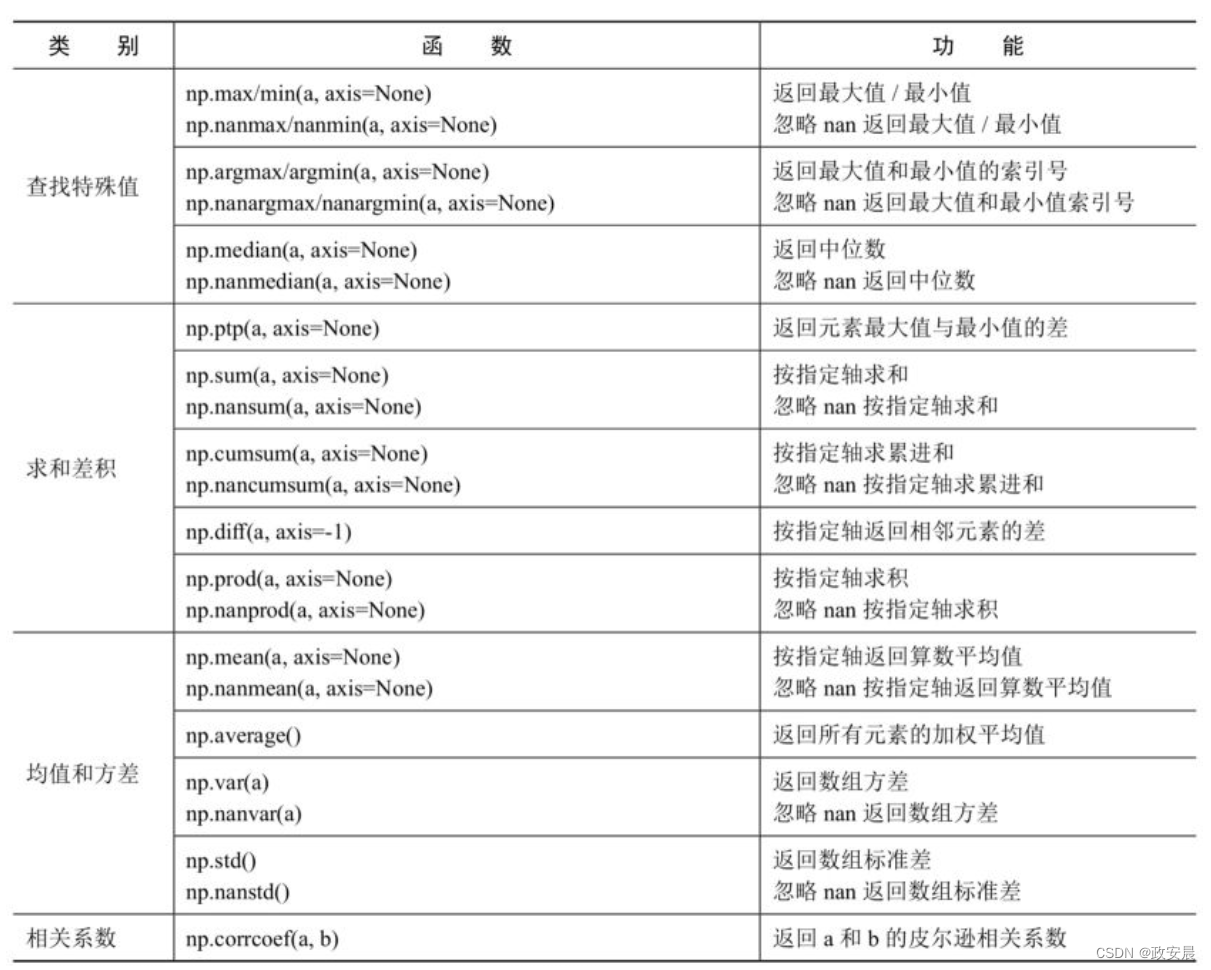
在实际应用中，我们所获得的数据远没有想象中的那么理想，存在缺值或无效值是常态。

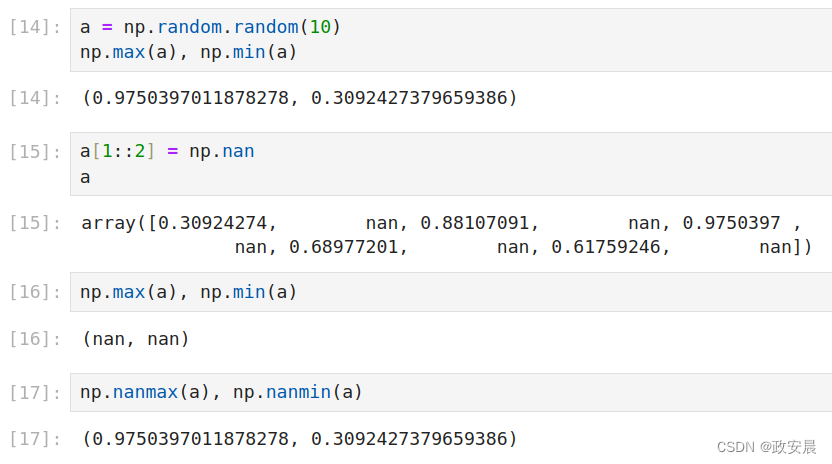
假定用np.nan表示无效值，一旦数据中存在无效值，对一个函数而言，是否忽略无效值将会得到完全不同的结果。下面先以求最大值和最小值为例，演示忽略np.nan的必要性。

a = np.random.random(10)
np.max(a), np.min(a)

# 将索引号为1、3、5、7、9的元素设置为np.nan
a[1::2] = np.nan 
a

# 此时，min()函数和max()函数失效了
np.max(a), np.min(a) 

# 必须使用nanmax()函数和nanmin()函数
np.nanmax(a), np.nanmin(a)

演绎如下：

方差和标准差是衡量数据离散程度最重要且最常用的指标，也是统计学上最重要的分析工具和手段，方差是各个数据与其算术平均值的离差平方和的平均值，方差的算术平方根，即为标准差。统计学上，方差和标准差使用比较频繁，下面来演示一下。

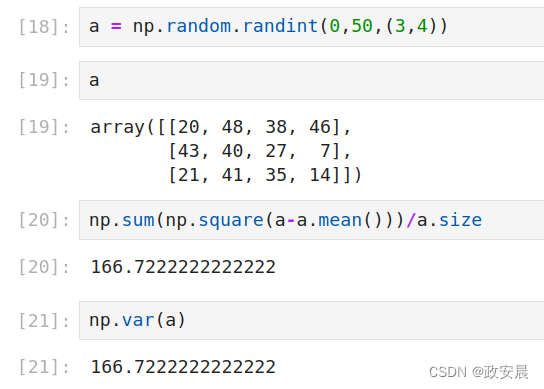
a = np.random.randint(0,50,(3,4))

# 用方差定义求方差
np.sum(np.square(a-a.mean()))/a.size 

# 直接用方差函数求方差，与用方差定义求方差的结果相同
np.var(a) 

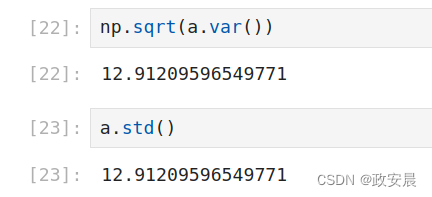
# 对方差求算术平方根就是标准差
np.sqrt(a.var()) 

# 直接用标准差函数求标准差，与对方差求算术平方根的结果相同
a.std()

示例演绎（方差）：

示例演绎（标准差）：

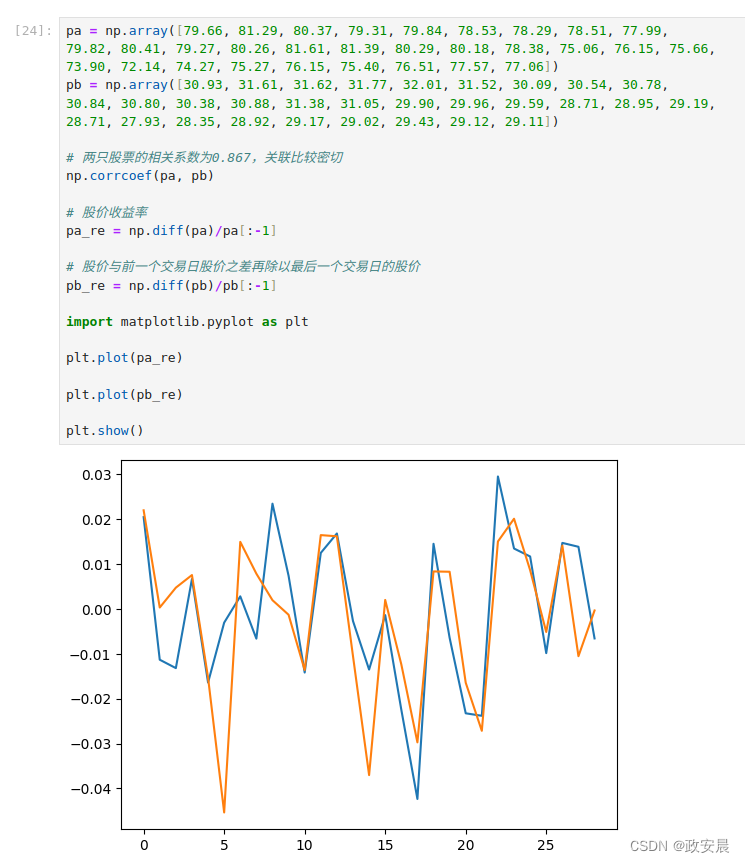
以下例子综合运用统计函数，来分析两只股票的关联关系和收益率。

pa和pb是两只股票连续30个交易日的股价数组，每日股价收益率定义为当日股价与前一个交易日股价之差再除以最后一个交易日的股价。

pa = np.array([79.66, 81.29, 80.37, 79.31, 79.84, 78.53, 78.29, 78.51, 77.99,
79.82, 80.41, 79.27, 80.26, 81.61, 81.39, 80.29, 80.18, 78.38, 75.06, 76.15, 75.66,
73.90, 72.14, 74.27, 75.27, 76.15, 75.40, 76.51, 77.57, 77.06])
pb = np.array([30.93, 31.61, 31.62, 31.77, 32.01, 31.52, 30.09, 30.54, 30.78,
30.84, 30.80, 30.38, 30.88, 31.38, 31.05, 29.90, 29.96, 29.59, 28.71, 28.95, 29.19,
28.71, 27.93, 28.35, 28.92, 29.17, 29.02, 29.43, 29.12, 29.11])

# 两只股票的相关系数为0.867，关联比较密切
np.corrcoef(pa, pb) 

# 股价收益率
pa_re = np.diff(pa)/pa[:-1] 

# 股价与前一个交易日股价之差再除以最后一个交易日的股价
pb_re = np.diff(pb)/pb[:-1] 

import matplotlib.pyplot as plt

plt.plot(pa_re)

plt.plot(pb_re)

plt.show()

演绎如下：

插值函数

数据插值是数据处理过程中经常用到的技术，常用的插值有一维插值、二维插值、高阶插值等，常见的算法有线性插值、B样条插值、临近插值等。

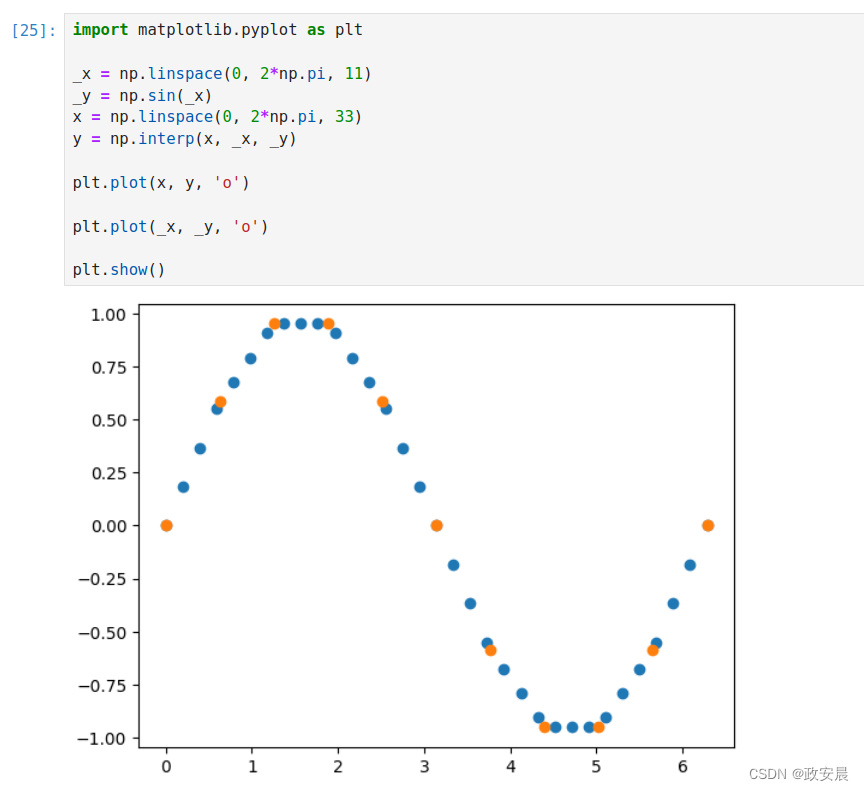
下面用一个实例来演示NumPy一维线性插值函数的使用方法。

假定_x和_y是原始的样本点x坐标和y坐标构成的数组，总数只有11个点。如果想在_x的值域范围内插值更多的点，如增加到33个点，就需要在_x的值域范围内生成33个点的x坐标构成的数组x，再利用插值函数np.interp( )得到对应的33个点的y坐标构成的数组y。

代码如下：

import matplotlib.pyplot as plt

_x = np.linspace(0, 2*np.pi, 11)
_y = np.sin(_x)
x = np.linspace(0, 2*np.pi, 33)
y = np.interp(x, _x, _y)

plt.plot(x, y, 'o')

plt.plot(_x, _y, 'o')

plt.show()

演绎如下：

多项式拟合函数

拟合与插值看起来有一些相似，所以初学者比较容易混淆，实际上二者是完全不同的概念，拟合又称回归，是指已知某函数的若干离散函数值，通过调整该函数中若干待定系数，使得该函数与已知离散函数值的误差达到最小。

多项式拟合是最常见的拟合方法。

对函数f(x)，我们可以使用一个k阶多项式去近似。

f(x)≈g(x)=a0+a1x+a2x2+a3x3+…+axxk通过选择合适的系数（最佳系数），可以使函数f(x)和g(x)之间的误差达到最小。

最小二乘法被用于寻找多项式的最佳系数。NumPy提供了一个非常简单易用的多项式拟合函数np.polyfit( )，只需要输入一组自变量的离散值，和一组对应的函数f(x)，并指定多项式次数k，就可以返回一组最佳系数，函数np.poly1d( )，则可以将一组最佳系数转成函数g(x)。

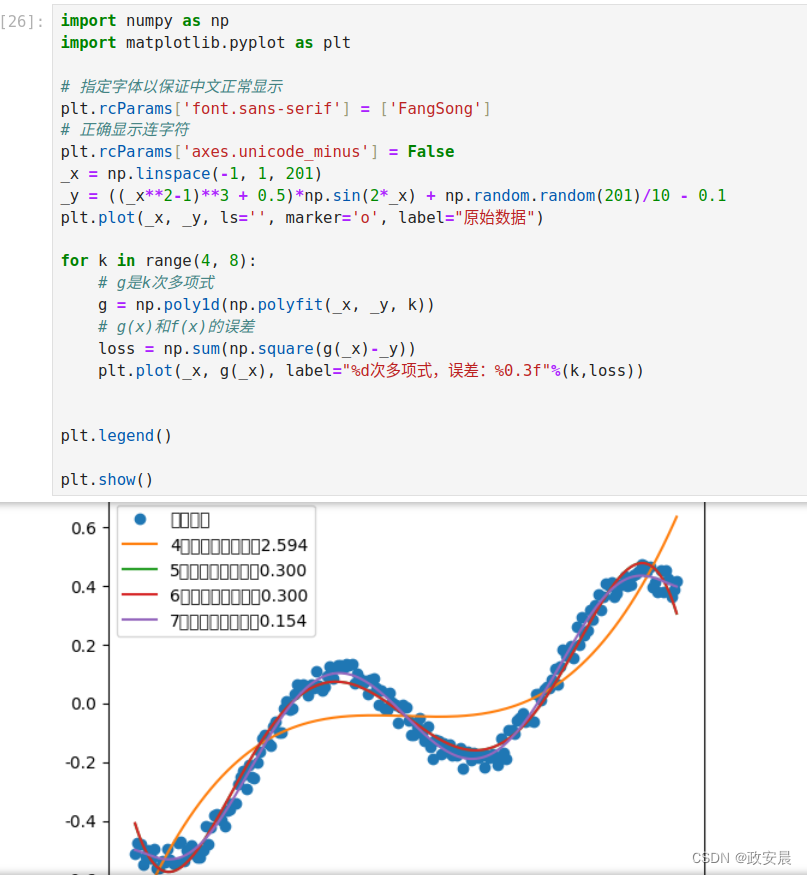
下述代码首先生成了原始数据点_x和_y，然后分别用4次、5次、6次和7次多项式去拟合原始数据，并计算出每次拟合的误差。

import numpy as np
import matplotlib.pyplot as plt

# 指定字体以保证中文正常显示
plt.rcParams['font.sans-serif'] = ['FangSong']
# 正确显示连字符
plt.rcParams['axes.unicode_minus'] = False 
_x = np.linspace(-1, 1, 201)
_y = ((_x**2-1)**3 + 0.5)*np.sin(2*_x) + np.random.random(201)/10 - 0.1
plt.plot(_x, _y, ls='', marker='o', label="原始数据")

for k in range(4, 8):
    # g是k次多项式
    g = np.poly1d(np.polyfit(_x, _y, k)) 
    # g(x)和f(x)的误差
    loss = np.sum(np.square(g(_x)-_y)) 
    plt.plot(_x, g(_x), label="%d次多项式，误差：%0.3f"%(k,loss))


plt.legend()

plt.show()

演绎如下：

这篇咱们先到这里，关于Numpy的函数方法部分就是这些了，下次咱们启动其它主题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1452062.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【数据结构之排序算法】

【数据结构之排序算法】

数据结构学习笔记---010 数据结构之排序算法1、排序的基本概念及其运用1.1、常见排序算法的实现2、插入排序的实现2.1、直接插入排序2.1.1、直接插入排序的实现2.1.1.1、直接插入排序InsertSort.h2.1.1.2、直接插入排序InsertSort.c2.1.1.3、直接插入排序main.c2.1.2、直接插入…
阅读更多...
BulingBuling - 《工作中的焦虑》 [ Anxiety at Work ]

BulingBuling - 《工作中的焦虑》 [ Anxiety at Work ]

工作中的焦虑 帮助团队建立复原力、处理不确定性和完成任务的8项策略 作者：阿德里安-戈斯蒂克、切斯特-埃尔顿和安东尼-戈斯蒂克 Anxiety at Work 8 Strategies to Help Teams Build Resilience, Handle Uncertainty, and Get Stuff Done By Adrian Gostick and…
阅读更多...
真实世界不存在了？OpenAI开年王炸，文字生成视频Sora公布

真实世界不存在了？OpenAI开年王炸，文字生成视频Sora公布

今天，OpenAI在毫无预兆的情况下，悄然更新了网站首页，公布了文字生成视频模型Sora。 我快速在OpenAI的网站上翻看了下，并未找到使用的入口，只能先通过官方文档了解具体的情况。 We’re teaching AI to understand and s…
阅读更多...
Vue核心基础3：计算属性和监视属性

Vue核心基础3：计算属性和监视属性

1 计算属性 这边以姓名案例&#xff0c;来介绍计算属性 <body><div id"root"><!-- 姓&#xff1a;<input type"text" v-model:value"firstName"><br>名&#xff1a;<input type"text" v-model:value&…
阅读更多...
人工智能学习与实训笔记（四）：神经网络之自然语言处理

人工智能学习与实训笔记（四）：神经网络之自然语言处理

目录 六、自然语言处理 6.1 词向量 (Word Embedding) 6.1.1 词向量的生成过程 6.1.2 word2vec介绍 6.1.3 word2vec&#xff1a;skip-gram算法的实现 6.2 句向量 - 情感分析 6.2.1 LSTM (Long Short-Term Memory)介绍 6.2.2 基于飞桨实现的情感分析模型 6.3 BERT 六、自…
阅读更多...
机器学习中7种常用的线性降维技术总结

机器学习中7种常用的线性降维技术总结

上篇文章中我们主要总结了非线性的降维技术&#xff0c;本文我们来总结一下常见的线性降维技术。 1、Principal Component Analysis (PCA) Principal Component Analysis (PCA) 是一种常用的降维技术&#xff0c;用于将高维数据集转换为低维表示&#xff0c;同时保留数据集的…
阅读更多...
【分享】JLINK的SW调试模式连线方式

【分享】JLINK的SW调试模式连线方式

大家知道&#xff0c;JLINK有2种调试模式&#xff1a;JTAG和SWD&#xff08;串行模式&#xff09;。 JTAG是常用模式&#xff0c;大家都熟悉、不废话了&#xff1b;如果使用SW模式&#xff0c;需要&#xff08;只需要&#xff09;4根连线&#xff0c;连接方式如下&#xff1a; …
阅读更多...
紫微斗数双星组合：天机天梁在辰戌

紫微斗数双星组合：天机天梁在辰戌

文章目录 前言内容总结 前言 紫微斗数双星组合&#xff1a;天机天梁在辰戌 内容 紫微斗数双星组合&#xff1a;天机天梁在辰戌 性格分析 在紫微斗数命盘中&#xff0c;天梁星是一颗“荫星”&#xff0c;能够遇难呈祥&#xff0c;化解凶危&#xff0c;主寿&#xff0c;主贵。…
阅读更多...
Sora和Pika，RunwayMl，Stable Video对比！网友：Sora真王者，其他都是弟

Sora和Pika，RunwayMl，Stable Video对比！网友：Sora真王者，其他都是弟

大家好&#xff0c;我是木易&#xff0c;一个持续关注AI领域的互联网技术产品经理&#xff0c;国内Top2本科&#xff0c;美国Top10 CS研究生&#xff0c;MBA。我坚信AI是普通人变强的“外挂”&#xff0c;所以创建了“AI信息Gap”这个公众号&#xff0c;专注于分享AI全维度知识…
阅读更多...
C++ “雪花算法“原理

C++ “雪花算法“原理

C雪花算法并不是传统的数据结构与算法而是一种崭新的分布式算法 属于深层次C 本篇文章就来描述一下雪花算法 什么是雪花算法: 雪花算法&#xff08;Snowflake&#xff09;是Twitter开源的一种分布式唯一ID生成算法。它可以在不依赖于数据库等其他存储设施的情况下&#xff0c…
阅读更多...
N-144基于微信小程序在线订餐系统

N-144基于微信小程序在线订餐系统

开发工具&#xff1a;IDEA、微信小程序 服务器&#xff1a;Tomcat9.0&#xff0c; jdk1.8 项目构建&#xff1a;maven 数据库&#xff1a;mysql5.7 前端技术&#xff1a;vue、ElementUI、 Vant Weapp 服务端技术&#xff1a;springbootmybatisredis 本系统分微信小程序和…
阅读更多...
自适应可爱卡通小人404页面模板

自适应可爱卡通小人404页面模板

一款可爱卡通小人的404网页&#xff0c;这个模板其实也很简洁。页面只是一张图片和两个按钮&#xff08;返回首页、联系站长&#xff09;&#xff0c;卡通小人还是有几分可爱的&#xff0c;对于对404页面没有其他特殊需求的朋友来说&#xff0c;有这样一个页面足矣&#xff0c;…
阅读更多...
Spring Resource

Spring Resource

java.net.URL 类可用于访问带有各种URL前缀的资源&#xff0c;但是对于访问一些资源还是不够方便。比如不能从类路径或者相对于ServletContext来获取资源。而Spring 的Resource接口&#xff0c;则可以通过类路径等方式来访问资源。 1 Resource接口 图 Resource接口及方法 getI…
阅读更多...
7.JS里表达式,if条件判断,三元运算符,switch语句,断点调试

7.JS里表达式,if条件判断,三元运算符,switch语句,断点调试

表达式和语句的区别 表达式就是可以被求值的代码比如什么a 1 语句就是一段可以执行的代码比如什么if else 直接给B站的黑马程序员的老师引流一波总结的真好 分支语句 就是基本上所有的语言都会有的if else 语句就是满足不同的条件执行不同的代码&#xff0c;让计算机有条件…
阅读更多...
MATLAB知识点：nchoosek函数（★★★☆☆）用来计算组合数，也能返回从向量v中抽取k个元素的所有组合

MATLAB知识点：nchoosek函数（★★★☆☆）用来计算组合数，也能返回从向量v中抽取k个元素的所有组合

讲解视频&#xff1a;可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。​ MATLAB教程新手入门篇&#xff08;数学建模清风主讲&#xff0c;适合零基础同学观看&#xff09;_哔哩哔哩_bilibili 节选自第3章&#xff1a;课后习题讲解中拓展的函数 在讲解第三…
阅读更多...
鸿蒙系统优缺点，能否作为开发者选择

鸿蒙系统优缺点，能否作为开发者选择

凡是都有对立面&#xff0c;就直接说说鸿蒙的优缺点吧。 鸿蒙的缺点&#xff1a; 鸿蒙是从2019年开始做出来的&#xff0c;那时候是套壳Android大家都知晓。从而导致大家不看鸿蒙系统&#xff0c;套壳Android就是多次一举。现在鸿蒙星河版已经是纯血鸿蒙&#xff0c;但是它的…
阅读更多...
云计算基础-云计算概念

云计算基础-云计算概念

云计算定义 云计算是一种基于互联网的计算方式&#xff0c;通过这种计算方式&#xff0c;共享的软硬件资源和信息可以按需提供给计算机和其他设备。云计算依赖资源共享以达成规模经济&#xff0c;类似基础设置(如电力网)。 云计算最基本的概念就是云加端&#xff0c;我们有一个…
阅读更多...
机器学习面试：请你谈谈逻辑回归的用法？

机器学习面试：请你谈谈逻辑回归的用法？

逻辑回归可用于以下几个方面: (1)用于概率预测。用于可能性预测时&#xff0c;得到的结果有可比性。比如根据模型进而预测在不同的自变量情况下&#xff0c;发生某病或某种情况的概率有多大。 (2)用于分类。实际上跟预测有些类似&#xff0c;也是根据模型&#xff0c;判断某人属…
阅读更多...
代码随想录第32天|● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II

代码随想录第32天|● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II

文章目录 买卖股票思路一&#xff1a;贪心代码&#xff1a; 思路&#xff1a;动态规划代码&#xff1a; 跳跃游戏思路&#xff1a;贪心找最大范围代码&#xff1a; 跳跃游戏②思路&#xff1a;代码&#xff1a; 方法二&#xff1a;处理方法一的特殊情况 买卖股票 思路一&#x…
阅读更多...
macOS 安装 conda

macOS 安装 conda

macOS 安装 conda 安装 conda参考 Conda是一个开源的软件包管理系统和环境管理系统&#xff0c;用于安装和管理软件包和其依赖项。 安装 conda mkdir miniconda3 cd miniconda3 bash Miniconda3-latest-MacOSX-x86_64.sh$ conda list参考 macOS 安装 conda开始使用conda
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023