虚拟化概述

虚拟化是一种资源管理技术，能够将计算机的各种实体资源（如CPU、内存、磁盘空间、网络适配器等）予以抽象、转换后呈现出来并可供分割、组合为一个或多个逻辑上的资源。这种技术通过在计算机硬件上创建一个抽象层，将单台计算机的硬件元素（处理器、内存、存储等）分成多个虚拟计算机（通常称为虚拟机 (VM)）。每个虚拟机都会运行自己的操作系统 (OS)，其行为就像一台独立的计算机，即使它只在一部分实际底层计算机硬件上运行。

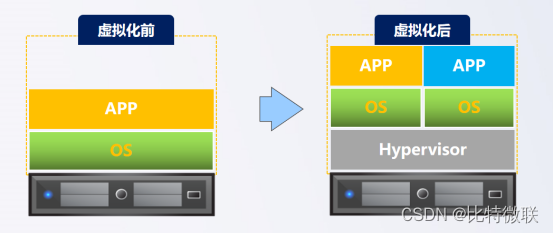
如下图，虚拟化前就是在物理服务器上安装操作系统，在操作系统中安装各种应用，企业中为了方便管理和业务隔离，一般一台服务器上只跑一个应用，比如专门一台服务器跑OA，另一台物理服务器上只跑WEB等等，即使该业务系统利用率很低，也必须是一台单独的物理服务器来支撑，这样就造成了资源利用率低，资源浪费的情况

而进行虚拟化后，相比与虚拟化前，服务器上装了一个虚拟化软件，英文名叫Hypervisor，有了Hypervisor之后就可以再物理机上同时创建多台虚拟机，给不同的虚拟机安装不同的操作系统和应用，通过hypervisor这一层就把传统的物理硬件跟上层的业务软件隔离开来，实现了解耦，同时多台不同的虚拟机就可以共用物理机的主机资源，提高了资源利用率，同时，不同的业务系统是跑在不同的虚拟机内的，同样也做到了业务隔离

虚拟化的几个概念

Guest OS：运行在物理机上的虚拟机的操作系统

Guest Machine：运行在物理机上的虚拟机

Hypervisor：VMM Hypervisor，又称虚拟机监视器（virtual machine monitor，缩写为VMM），未来虚拟机就是靠它来运行的，它可以跑在物理机上，也可以跑在宿主机的操作系统上

Host OS：运行在物理机(宿主机)上的操作系统

Host Machine：物理机、宿主机

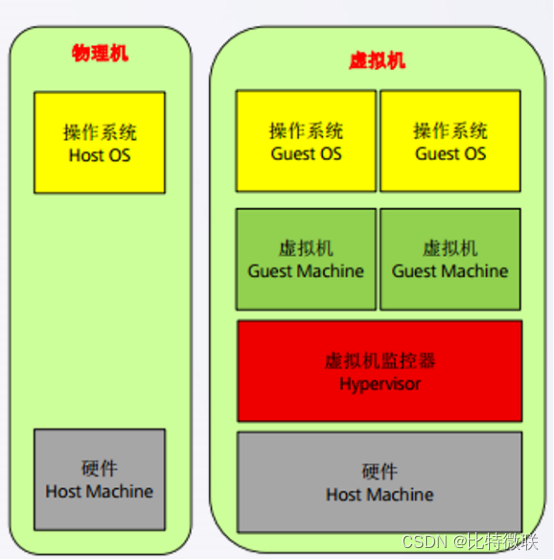
Hypervisor架构

计算虚拟化的软件层，通常叫Hypervisor，即虚拟化层，也叫虚拟机监控器（Virtual Machine Monitor，VMM），负责GuestOS所有硬件资源调用

常见的Hypervisor架构有两种：

· TYPE-I（裸金属架构）：VMM直接运行在裸机上，使用和管理底层硬件资源，Guest OS对硬件资源访问都需要通过VMM完成，VMM拥有硬件驱动程序。如CNA，ESXI等

· TYPE-II（宿主型、主机型）：VMM之下还有一层宿主操作系统，Guest OS对硬件资源访问必须经过宿主操作系统，带来额外开销，所有硬件驱动、内存管理、进程调度等有宿主操作系统执行。如VMware Workstation、oracke VirtualBox等

Hypervisor架构对比

宿主架构：底层是硬件如CPU、内存、硬盘等，在硬件之上我们给电脑装了操作系统，比如Windows10，有了主机操作系统之后就可以装各种应用了，如QQ、微信等（APPllcation），而Hypervisor也可以作为一种应用，虚拟化软件也是操作系统上的应用，比如安装了VMware Workstation，有了虚拟化软件之后就可以起各种虚拟机，有了虚机之后就可以给虚拟机安装Guest OS

裸金属架构：最底层也是硬件，但是在硬件之上没有安装操作系统，而是直接安装了Virtualization Layer，相当于直接在硬件上安装了Hypervisor，在硬件上安装了hypervisor之后就可以直接创建虚拟机，然后给不同虚拟机安装不同的Guest OS

裸金属架构和宿主架构的区别

简而言之裸金属架构和宿主架构最大的区别是在硬件之上是否安装了操作系统，宿主架构是先安装操作系统再安装虚拟化软件，裸金属架构是直接再硬件上安装Hypervisor

裸金属架构和宿主架构的优劣势对比

宿主架构优势：宿主架构再硬件上安装了操作系统，底层硬件的驱动由操作HOST OS提供，比如我们的Windows电脑，底层硬件的驱动都是由windows来解决，这样来说，虚拟化软件跟底层的硬件之间就分开了，虚拟化软件不论底层的硬件是什么都是可以运行的，这样依赖宿主型架构系统的适配性就很强

宿主架构缺点：Host OS运行在硬件之上，主机操作系统本身会占用一定的CPU、内存和硬盘资源，宿主型架构的资源利用率是比较低的

裸金属架构优势：在硬件上并没有装操作系统，没有主机操作系统来占用过多的CPU、内存、硬件资源，底层硬件资源利用率比宿主架构高

裸金属架构劣势：裸金属架构在硬件上直接要装Hypervisor，那底层这些硬件的驱动就要由Hypervisor来解决，但是Hypervisor是一个虚拟化软件，这就意味着，其实在裸金属架构的Hypervisor中由非常小的操作系统内核，这个操作系统内核里面是包含了底层硬件的驱动的，但是由于非常小的操作系统内核的大小有限，它能够携带的驱动程序也是有限，这就意味着裸金属架构的情形下，它对于底层硬件是有要求的，裸金属架构所需的CPU、内存、硬盘、主板、网卡等硬件必须是hypervisor所携带的驱动的范围内，所以裸金属架构对于硬件的适配性不强，它对于硬件是有明确需求的