
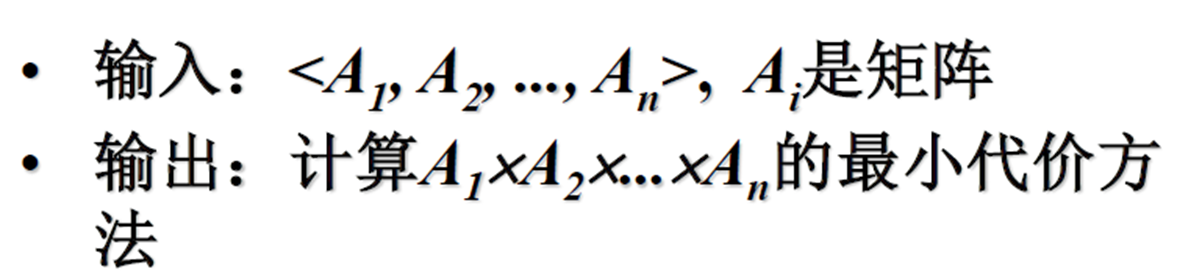
明确原始问题A[1:n]:计算矩阵链
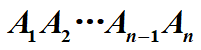
所需的最小乘法次数。
(1)是否满足最优子结构,问题的解是否包含子问题的优化解?
若计算A[1:n]的优化顺序在k处断开矩阵链,即A[1:n]=A[1:k]×A[k+1:n],则在A[1:n]的优化顺序中,对应于子问题A[1:k]的解必须是A[1:k]的优化解,对应A[k+1:n]的解必须是A[k+1:n]的优化解。
(2)是否满足重叠子问题?
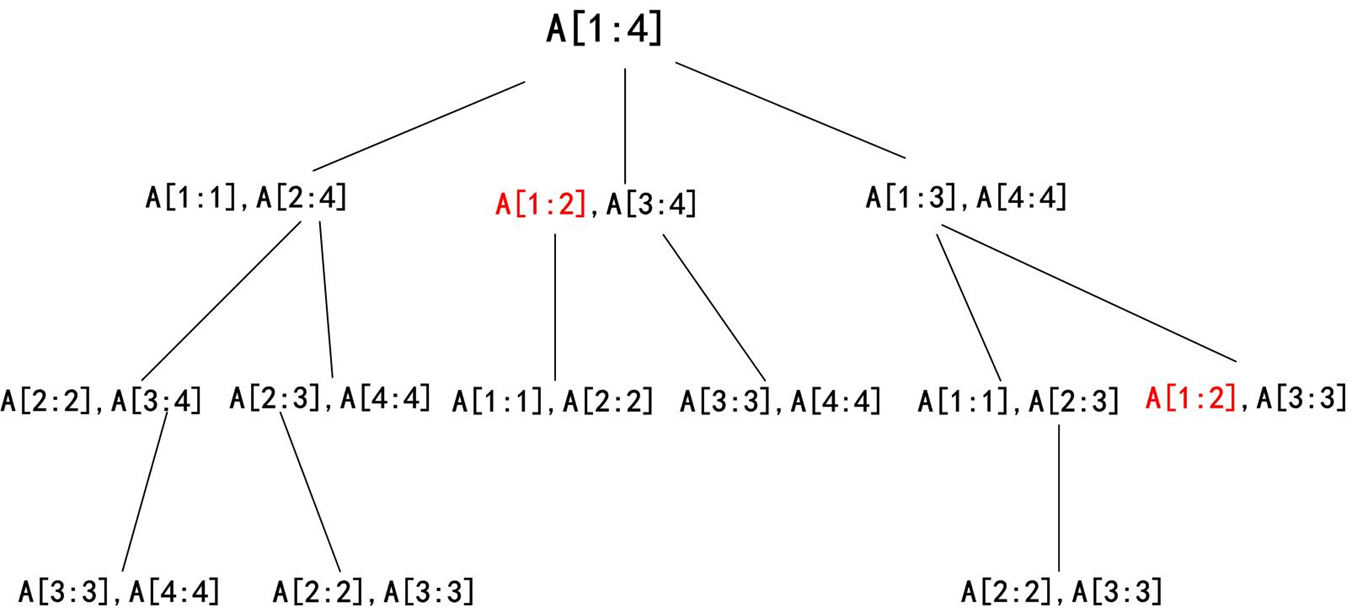
如A[1:2]计算了2次,保存下来能够节省计算时间;
递归计算时,很多子问题会被重复计算很多次。这也是应用动态规划的特征之一
1.分析优化解的结构

2.递归定义最优解的代价

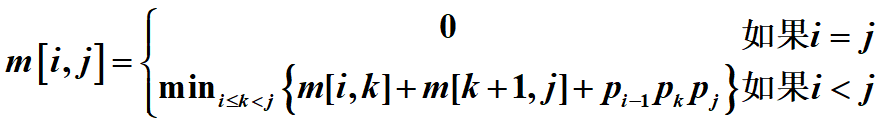
3.自底向上计算最优代价
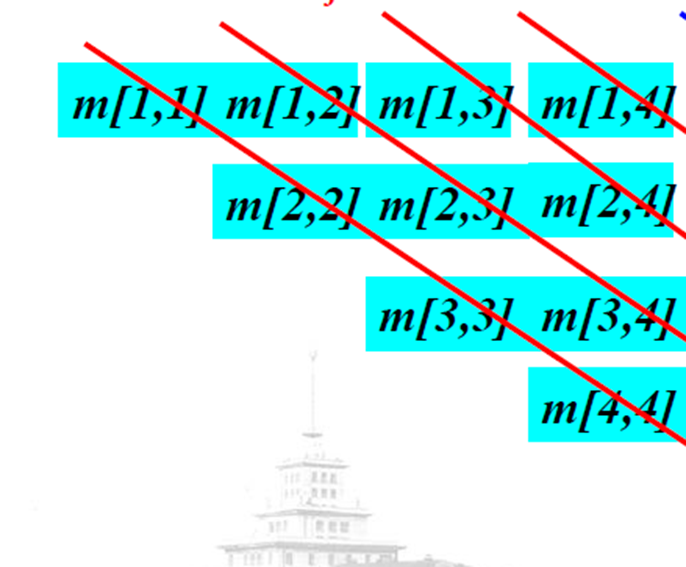
沿对角线的方式填表!!先计算m[1,1]对角线,再计算m[1,2]对角线,以此类推,最后得到m[1,4],这就是一个自底向上的过程!
4.利用最优值的信息构造最优解
取得的k为A[i:j]最优次序中的断开位置,也即是加括号的位置,记录到s[i][j]表中。
原始问题为A[1:n],通过回溯追踪获得A[1:n]最优值时的k值,即可获得所有加括号的位置。
伪代码:

时间复杂度是O(n^3)
例题:
对维数为序列<5, 10, 3, 12, 5, 50, 6>的各矩阵,找出 矩阵链乘积的一个最优加全部括号

关键在于计算出两个表格:m[i,j]和 s[i,j] (本题都是6行6列)
i = j 时,m[i,j] = 0,所以m[1,1] = 0, m[2,2] = 0,m[3,3] = 0,m[4,4] = 0, m[5,5] = 0, m[6,6] = 0;
m[1,2] = min{ k=1, m[1,1] + m[2,2] + p0p1p2 = 0+0+5*10*3 } = 150;m[2,3] = min{ k=2, m[2,2] + m[3,3] + p1p2p3 = 0+0+10*3*12 } = 360;
m[3,4] = min{ k=3, m[3,3] + m[4,4] + p2p3p4 = 0+0+3*12*5 } = 180;
m[4,5] = min{ k=4, m[4,4] + m[5,5] + p3p4p5 = 0+0+12*5*50 } = 3000;
m[5,6] = min{ k=5, m[5,5] + m[6,6] + p4p5p6 = 0+0+5*50*6 } = 1500;
m[1,3] = min{ k=1, m[1,1] + m[2,3] + p0p1p3 = 0+360+600= 960 ;
k=2, m[1,2] + m[3,3] + p0p2p3 = 150+0+5*3*12 = 330} = 330;
m[2,4] = min{ k=2, m[2,2] + m[3,4] + p1p2p4 = 0+180+10*3*5 = 330;
k=3, m[2,3] + m[4,4] + p1p3p4 = 0+360+0+10*12*5=960} = 330;
m[3,5] = min{ k=3, m[3,3] + m[4,5] + p2p3p5 = 0+3000+3*12*50 = 4800;
k=4, m[3,4] + m[5,5] + p2p4p5 = 180+0+3*5*50 = 930} = 930;
m[4,6] = min{ k=4, m[4,4] + m[5,6] + p3p4p6 = 0+1500+12*5*6 = 1860;
k=5, m[4,5] + m[6,6] + p3p5p6 = 3000+0+12*50*6 = 6600} = 1860;
后面以此类推:......

m[i, j]:记录子问题最优解的解值,保存下来避免重复计算。即矩阵连乘积A[i, j]的最小值。
| i / j | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 150 | 330 | 405 | 1655 | 2010 |
| 2 | 0 | 360 | 330 | 1080 | 1950 | |
| 3 | 0 | 180 | 930 | 1770 | ||
| 4 | 0 | 3000 | 1860 | |||
| 5 | 0 | 1500 | ||||
| 6 | 0 |
s[i, j]:记录A[i, j]最优次序的断开位置,就是 k 的最优值。
| i / j | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 2 | 2 | 4 | 2 |
| 2 | 0 | 2 | 2 | 2 | 2 | |
| 3 | 0 | 3 | 4 | 4 | ||
| 4 | 0 | 4 | 4 | |||
| 5 | 0 | 5 | ||||
| 6 | 0 |
所矩阵A1A2A3A4A5A6, 即矩阵连乘积A[1,6]的最少次数 = 2010;
s[1,6] = 2,A1A2A3A4A5A6 = (A1A2)A3A4A5A6;
s[3,6] = 4,A3A4A5A6 = (A3A4)(A5A6);
综上,A1A2A3A4A5A6 = (A1A2)( (A3A4)(A5A6) );





![[VP]河南第十三届ICPC大学生程序竞赛 L.手动计算](https://img-blog.csdnimg.cn/adace8a661994a7898be25677db546a2.png)