前言

传送门 :

题意 :
给定两个椭圆 的方程 , 要求 求出椭圆并集的面积之和

思路 :
本题很显然是积分 或者 计算几何的问题

对于积分的做法, 无非就是根据积分公式求出第一象限的面积 之后拓展到后面四个象限。(奈何我懒, 连两个椭圆的焦点都不想求更别提后面的积分公式了)

官方题解用的是蒙特卡洛积分的方法 , 这个方法的证明就是大数定理 。

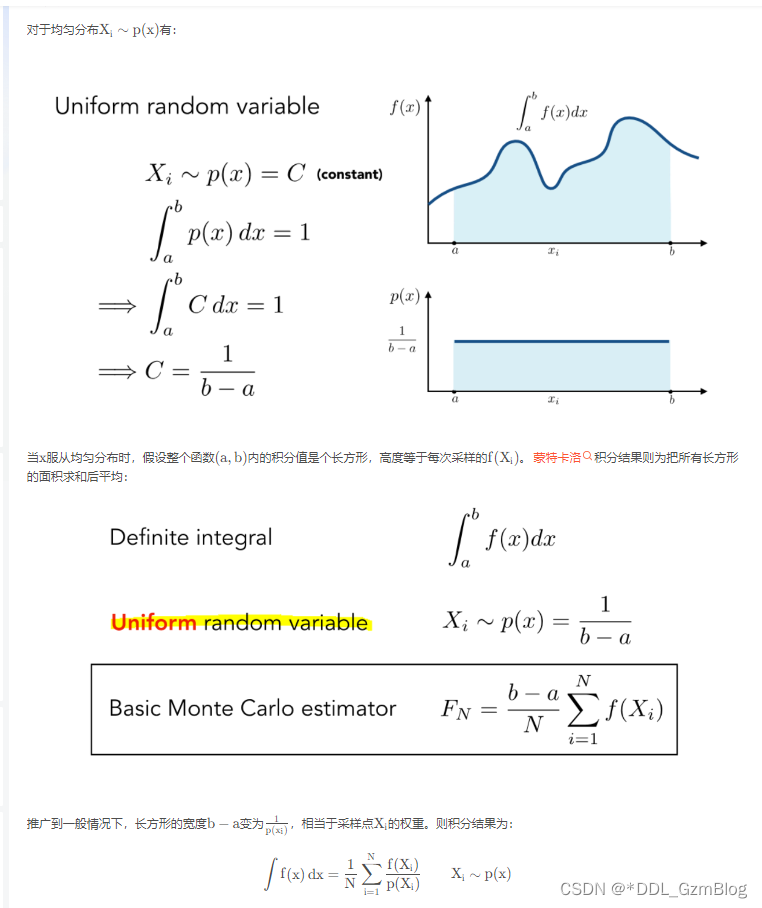
根据这几个公式的推导 , 那么我们可以知道 定积分形式的内容就可以转变为$\frac{1}{N}\sum \frac{f(x)}{p(x)}$ 的形式 , 即最后变成了面积的比

那么这个公式的精度如何 , 下面是$y=f(x)$在$[0,1]$区间上面的分布 因此我们可以认为在$10^5$的级别精度是可行的

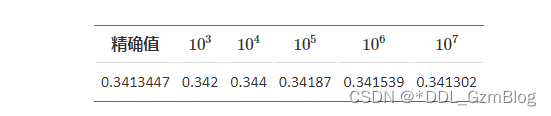
code :

double a1,b1,a2,b2;
double cnt ;

void solve(){
	cnt = 0 ;
	
	cin>>a1>>b1>>a2>>b2;
	for(double i =  -8; i <= 8 ; i += 0.01){
		for(double j = -8 ; j <= 8 ;j += 0.01){
			if(i*i/a1/a1 + j*j/b1/b1 <=1 || i*i/a2/a2 + j*j/b2/b2 <= 1){
						cnt ++ ;	
			}
		}
	}
	
	cnt = (cnt*16*16/(1600*1600));//面积之比
	printf("%.1f\n" , cnt);
}