题目： 一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。
题目分析：

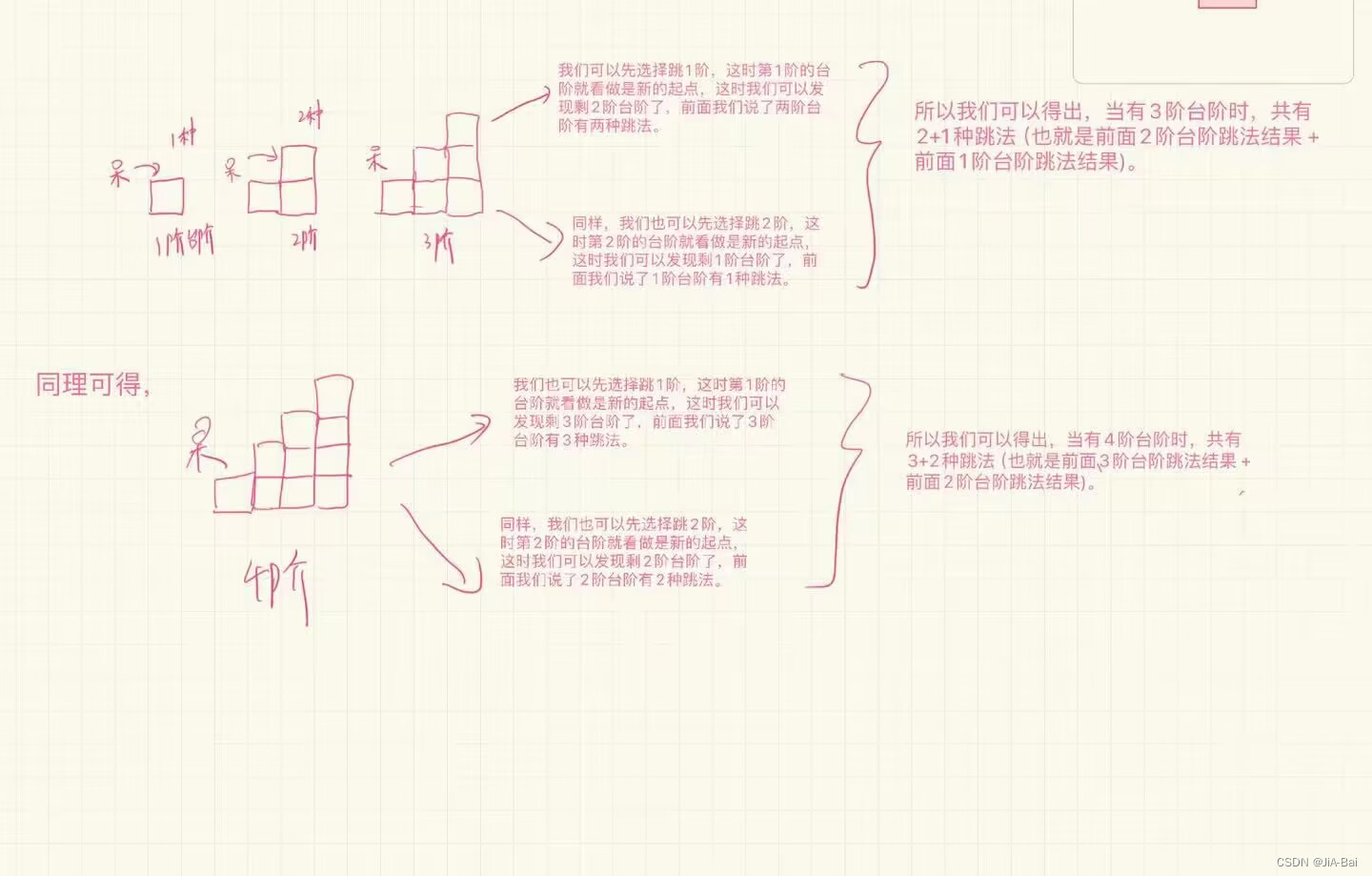
1. 如下图所示，当只有一阶台阶时，青蛙只有一种跳法。
2. 当只有两阶台阶时，青蛙有两种算法，也就是一次跳一个或者直接跳两个。
3. 但当有三阶台阶时，我们此时：
   （1）可以先选择跳1阶，这时第1阶的台阶就看做是新的起点，这时我们可以发现剩2阶台阶了，前面我们说了两阶台阶有两种跳法。
   （2）同样，也可以先选择跳2阶，这时第2阶的台阶就看做是新的起点，这时我们可以发现剩1阶台阶了，前面我们说了1阶台阶有1种跳法。
   （3）所以我们可以得出，当有3阶台阶时，共有2+1种跳法（也就是前面2阶台阶跳法结果 + 前面1阶台阶跳法结果)。
4. 同理，当有四阶台阶时，我们此时：
   （1）可以先选择跳1阶，这时第1阶的台阶就看做是新的起点，这时我们可以发现剩3阶台阶了，前面我们说了3阶台阶有3种跳法。
   （2）同样，也可以先选择跳2阶，这时第2阶的台阶就看做是新的起点，这时我们可以发现剩2阶台阶了，前面我们说了2阶台阶有2种跳法。
   （3）所以我们可以得出，当有3阶台阶时，共有3+2种跳法（也就是前面3阶台阶跳法结果 + 前面2阶台阶跳法结果)。

总结： 说白了上面过程其实就是用前面的结果，来快速得到下一步的结果。

分析完题目我们就可以写代码了，实现代码如下所示：
方法一：递归实现

public class test2{
    public static int jump(int n) {
        if(n == 1){
            return 1;
        }else if(n == 2){
            return 2;
        }else{
            return jump(n-1) + jump(n-2);
        }

    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        System.out.println(jump(n));
    }
}

方法二：非递归实现（用数组）

public class test2{
    public static void main(String[] args) {
        int n = 5;
        int[] array = new int[n];
        array[0] = 1;
        array[1] = 2;
        for (int i = 2; i < n; i++) {
            array[i]= array[i-1] + array[i-2];
            System.out.println(i+1+"阶"+array[i]+"种跳法");
        }
    }
}