PyTorch 2.2 中文官方教程（二）

在 YouTube 上介绍 PyTorch

PyTorch 介绍 - YouTube 系列

原文：pytorch.org/tutorials/beginner/introyt.html

译者：飞龙

协议：CC BY-NC-SA 4.0

介绍 || 张量 || 自动微分 || 构建模型 || TensorBoard 支持 || 训练模型 || 模型理解

作者：Brad Heintz

本教程与 YouTube 上的PyTorch 初学者系列一起进行。

本教程假定您对 Python 和深度学习概念有基本了解。

运行教程代码

您可以通过以下几种方式运行本教程：

在云端：这是最简单的入门方式！每个部分顶部都有一个 Colab 链接，点击后会在完全托管的环境中打开一个带有代码的笔记本。专业提示：使用带有 GPU 运行时的 Colab 可以加快操作速度 运行时 > 更改运行时类型 > GPU
本地：此选项需要您首先在本地机器上设置 PyTorch 和 torchvision（安装说明）。下载笔记本或将代码复制到您喜欢的 IDE 中。

PyTorch 介绍
PyTorch 张量介绍
自动微分的基础知识
使用 PyTorch 构建模型
PyTorch TensorBoard 支持
使用 PyTorch 进行训练
使用 Captum 理解模型

PyTorch 简介

原文：pytorch.org/tutorials/beginner/introyt/introyt1_tutorial.html

译者：飞龙

协议：CC BY-NC-SA 4.0

注意

点击这里下载完整的示例代码

简介 || 张量 || Autograd || 构建模型 || TensorBoard 支持 || 训练模型 || 模型理解

跟随下面的视频或在youtube上跟随。

www.youtube.com/embed/IC0_FRiX-sw

PyTorch 张量

跟随视频从03:50开始。

首先，我们将导入 pytorch。

import torch

让我们看一些基本的张量操作。首先，只是创建张量的几种方法：

z = torch.zeros(5, 3)
print(z)
print(z.dtype)

tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
torch.float32

上面，我们创建了一个填充了零的 5x3 矩阵，并查询其数据类型，以找出这些零是 32 位浮点数，这是 PyTorch 的默认值。

如果你想要整数怎么办？你总是可以覆盖默认值：

i = torch.ones((5, 3), dtype=torch.int16)
print(i)

tensor([[1, 1, 1],
        [1, 1, 1],
        [1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]], dtype=torch.int16)

你可以看到当我们改变默认值时，张量在打印时会报告这一点。

通常会随机初始化学习权重，通常使用特定的种子为 PRNG 以便结果可重现：

torch.manual_seed(1729)
r1 = torch.rand(2, 2)
print('A random tensor:')
print(r1)

r2 = torch.rand(2, 2)
print('\nA different random tensor:')
print(r2) # new values

torch.manual_seed(1729)
r3 = torch.rand(2, 2)
print('\nShould match r1:')
print(r3) # repeats values of r1 because of re-seed

A random tensor:
tensor([[0.3126, 0.3791],
        [0.3087, 0.0736]])

A different random tensor:
tensor([[0.4216, 0.0691],
        [0.2332, 0.4047]])

Should match r1:
tensor([[0.3126, 0.3791],
        [0.3087, 0.0736]])

PyTorch 张量直观地执行算术运算。形状相似的张量可以相加、相乘等。与标量的操作分布在张量上：

ones = torch.ones(2, 3)
print(ones)

twos = torch.ones(2, 3) * 2 # every element is multiplied by 2
print(twos)

threes = ones + twos       # addition allowed because shapes are similar
print(threes)              # tensors are added element-wise
print(threes.shape)        # this has the same dimensions as input tensors

r1 = torch.rand(2, 3)
r2 = torch.rand(3, 2)
# uncomment this line to get a runtime error
# r3 = r1 + r2

tensor([[1., 1., 1.],
        [1., 1., 1.]])
tensor([[2., 2., 2.],
        [2., 2., 2.]])
tensor([[3., 3., 3.],
        [3., 3., 3.]])
torch.Size([2, 3])

这里是一小部分可用的数学运算：

r = (torch.rand(2, 2) - 0.5) * 2 # values between -1 and 1
print('A random matrix, r:')
print(r)

# Common mathematical operations are supported:
print('\nAbsolute value of r:')
print(torch.abs(r))

# ...as are trigonometric functions:
print('\nInverse sine of r:')
print(torch.asin(r))

# ...and linear algebra operations like determinant and singular value decomposition
print('\nDeterminant of r:')
print(torch.det(r))
print('\nSingular value decomposition of r:')
print(torch.svd(r))

# ...and statistical and aggregate operations:
print('\nAverage and standard deviation of r:')
print(torch.std_mean(r))
print('\nMaximum value of r:')
print(torch.max(r))

A random matrix, r:
tensor([[ 0.9956, -0.2232],
        [ 0.3858, -0.6593]])

Absolute value of r:
tensor([[0.9956, 0.2232],
        [0.3858, 0.6593]])

Inverse sine of r:
tensor([[ 1.4775, -0.2251],
        [ 0.3961, -0.7199]])

Determinant of r:
tensor(-0.5703)

Singular value decomposition of r:
torch.return_types.svd(
U=tensor([[-0.8353, -0.5497],
        [-0.5497,  0.8353]]),
S=tensor([1.1793, 0.4836]),
V=tensor([[-0.8851, -0.4654],
        [ 0.4654, -0.8851]]))

Average and standard deviation of r:
(tensor(0.7217), tensor(0.1247))

Maximum value of r:
tensor(0.9956)

关于 PyTorch 张量的强大功能还有很多要了解，包括如何设置它们以在 GPU 上进行并行计算 - 我们将在另一个视频中深入探讨。

PyTorch 模型

跟随视频从10:00开始。

让我们谈谈如何在 PyTorch 中表达模型

import torch                     # for all things PyTorch
import torch.nn as nn            # for torch.nn.Module, the parent object for PyTorch models
import torch.nn.functional as F  # for the activation function

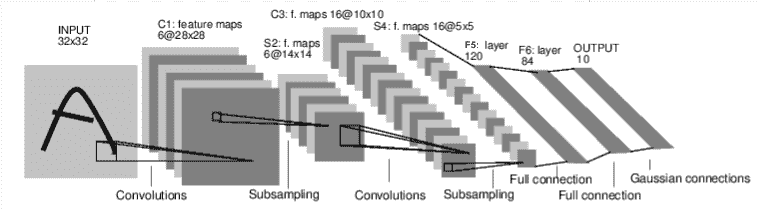
le-net-5 diagram

图：LeNet-5

上面是 LeNet-5 的图表，这是最早的卷积神经网络之一，也是深度学习爆炸的推动力之一。它被设计用来读取手写数字的小图像（MNIST 数据集），并正确分类图像中代表的数字。

这是它的简化版本是如何工作的：

层 C1 是一个卷积层，意味着它在输入图像中扫描在训练期间学到的特征。它输出一个地图，显示它在图像中看到每个学到的特征的位置。这个“激活图”在 S2 层中进行降采样。
层 C3 是另一个卷积层，这次是扫描 C1 的激活图以查找特征的组合。它还输出描述这些特征组合的空间位置的激活图，在 S4 层中进行降采样。
最后，最后的全连接层 F5、F6 和 OUTPUT 是一个分类器，它接收最终的激活图，并将其分类为表示 10 个数字的十个箱子之一。

我们如何用代码表达这个简单的神经网络？

class LeNet(nn.Module):

    def __init__(self):
        super(LeNet, self).__init__()
        # 1 input image channel (black & white), 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)  # 5*5 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

查看这段代码，你应该能够发现与上面图表的一些结构相似之处。

这展示了典型 PyTorch 模型的结构：

它继承自torch.nn.Module - 模块可以嵌套 - 实际上，甚至Conv2d和Linear层类也继承自torch.nn.Module。
模型将有一个__init__()函数，在其中实例化其层，并加载可能需要的任何数据工件（例如，NLP 模型可能加载一个词汇表）。
模型将有一个forward()函数。这是实际计算发生的地方：输入通过网络层和各种函数生成输出。
除此之外，你可以像构建任何其他 Python 类一样构建你的模型类，添加任何你需要支持模型计算的属性和方法。

让我们实例化这个对象并运行一个样本输入。

net = LeNet()
print(net)                         # what does the object tell us about itself?

input = torch.rand(1, 1, 32, 32)   # stand-in for a 32x32 black & white image
print('\nImage batch shape:')
print(input.shape)

output = net(input)                # we don't call forward() directly
print('\nRaw output:')
print(output)
print(output.shape)

LeNet(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

Image batch shape:
torch.Size([1, 1, 32, 32])

Raw output:
tensor([[ 0.0898,  0.0318,  0.1485,  0.0301, -0.0085, -0.1135, -0.0296,  0.0164,
          0.0039,  0.0616]], grad_fn=<AddmmBackward0>)
torch.Size([1, 10])

上面发生了一些重要的事情：

首先，我们实例化LeNet类，并打印net对象。torch.nn.Module的子类将报告它已创建的层及其形状和参数。如果您想要了解其处理过程的要点，这可以提供一个方便的模型概述。

在下面，我们创建一个代表具有 1 个颜色通道的 32x32 图像的虚拟输入。通常，您会加载一个图像块并将其转换为这种形状的张量。

您可能已经注意到我们的张量有一个额外的维度 - 批处理维度。PyTorch 模型假定它们正在处理数据批次 - 例如，我们的图像块批次中的 16 个图像将具有形状(16, 1, 32, 32)。由于我们只使用一个图像，我们创建一个形状为(1, 1, 32, 32)的批次。

我们通过像调用函数一样调用模型来请求推理：net(input)。此调用的输出表示模型对输入表示特定数字的信心程度。（由于此模型的实例尚未学习任何内容，我们不应该期望在输出中看到任何信号。）查看output的形状，我们可以看到它还具有一个批处理维度，其大小应始终与输入批处理维度匹配。如果我们传入了一个包含 16 个实例的输入批次，output的形状将为(16, 10)。

数据集和数据加载器

从14:00开始观看视频。

接下来，我们将演示如何使用 TorchVision 中准备好下载的开放访问数据集，将图像转换为模型可消费的形式，并如何使用 DataLoader 将数据批量提供给模型。

我们需要做的第一件事是将我们的输入图像转换为 PyTorch 张量。

#%matplotlib inline

import torch
import torchvision
import torchvision.transforms as transforms

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2470, 0.2435, 0.2616))])

在这里，我们为我们的输入指定了两个转换：

transforms.ToTensor() 将由 Pillow 加载的图像转换为 PyTorch 张量。

transforms.Normalize() 调整张量的值，使其平均值为零，标准差为 1.0。大多数激活函数在 x = 0 附近具有最强的梯度，因此将数据居中在那里可以加快学习速度。传递给变换的值是数据集中图像的 rgb 值的平均值（第一个元组）和标准差（第二个元组）。您可以通过运行以下几行代码自己计算这些值：


from torch.utils.data import ConcatDataset transform = transforms.Compose([transforms.ToTensor()]) trainset = torchvision.datasets.CIFAR10(root='./data', train=True,

> download=True, transform=transform)
> 
#将所有训练图像堆叠在一起，形成形状为(50000, 3, 32, 32)的张量 x = torch.stack([sample[0] for sample in ConcatDataset([trainset])])

#获取每个通道的平均值 mean = torch.mean(x, dim=(0,2,3)) #tensor([0.4914, 0.4822, 0.4465]) std = torch.std(x, dim=(0,2,3)) #tensor([0.2470, 0.2435, 0.2616])

还有许多其他可用的转换，包括裁剪、居中、旋转和反射。

接下来，我们将创建一个 CIFAR10 数据集的实例。这是一个代表 10 类对象的 32x32 彩色图像块的集合：6 种动物（鸟、猫、鹿、狗、青蛙、马）和 4 种车辆（飞机、汽车、船、卡车）：

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)

Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data/cifar-10-python.tar.gz

  0%|          | 0/170498071 [00:00<?, ?it/s]
  0%|          | 425984/170498071 [00:00<00:42, 4044472.50it/s]
  2%|2         | 4063232/170498071 [00:00<00:07, 22577866.17it/s]
  6%|5         | 9404416/170498071 [00:00<00:04, 36369973.58it/s]
  8%|8         | 13762560/170498071 [00:00<00:04, 39105082.28it/s]
 11%|#1        | 19005440/170498071 [00:00<00:03, 43825417.38it/s]
 14%|#3        | 23429120/170498071 [00:00<00:03, 43818360.32it/s]
 17%|#6        | 28639232/170498071 [00:00<00:03, 46489541.28it/s]
 20%|#9        | 33325056/170498071 [00:00<00:02, 45786944.87it/s]
 23%|##2       | 38567936/170498071 [00:00<00:02, 47766940.54it/s]
 25%|##5       | 43384832/170498071 [00:01<00:02, 46754502.74it/s]
 28%|##8       | 48562176/170498071 [00:01<00:02, 48195537.67it/s]
 31%|###1      | 53411840/170498071 [00:01<00:02, 46939745.24it/s]
 35%|###4      | 59506688/170498071 [00:01<00:02, 51037365.18it/s]
 39%|###9      | 67108864/170498071 [00:01<00:01, 58314403.51it/s]
 45%|####5     | 77168640/170498071 [00:01<00:01, 70815830.81it/s]
 50%|#####     | 86016000/170498071 [00:01<00:01, 76062449.51it/s]
 56%|#####6    | 96239616/170498071 [00:01<00:00, 83839821.30it/s]
 62%|######1   | 105283584/170498071 [00:01<00:00, 85769908.93it/s]
 68%|######7   | 115474432/170498071 [00:01<00:00, 90570010.64it/s]
 73%|#######3  | 124551168/170498071 [00:02<00:00, 90287482.99it/s]
 79%|#######8  | 134545408/170498071 [00:02<00:00, 93132654.68it/s]
 84%|########4 | 143884288/170498071 [00:02<00:00, 92481450.08it/s]
 90%|########9 | 153157632/170498071 [00:02<00:00, 92207858.35it/s]
 95%|#########5| 162398208/170498071 [00:02<00:00, 74753698.93it/s]
100%|#########9| 170426368/170498071 [00:02<00:00, 64194917.16it/s]
100%|##########| 170498071/170498071 [00:02<00:00, 63329744.47it/s]
Extracting ./data/cifar-10-python.tar.gz to ./data

注意

当您运行上面的单元格时，数据集下载可能需要一些时间。

这是在 PyTorch 中创建数据集对象的一个示例。可下载的数据集（如上面的 CIFAR-10）是torch.utils.data.Dataset的子类。PyTorch 中的Dataset类包括 TorchVision、Torchtext 和 TorchAudio 中的可下载数据集，以及实用程序数据集类，如torchvision.datasets.ImageFolder，它将读取一个带有标签的图像文件夹。您还可以创建自己的Dataset子类。

当我们实例化数据集时，我们需要告诉它一些事情：

我们希望数据存储的文件系统路径。
无论我们是否将此集合用于训练；大多数数据集都将被分割为训练和测试子集。
如果我们还没有下载数据集，我们是否想要下载数据集。
我们想要应用于数据的转换。

一旦您的数据集准备好了，您可以将其提供给DataLoader：

trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

Dataset子类包装对数据的访问，并专门针对其提供的数据类型。DataLoader对数据一无所知，但会根据您指定的参数将Dataset提供的输入张量组织成批次。

在上面的示例中，我们要求DataLoader从trainset中给我们提供 4 个图像的批次，随机化它们的顺序（shuffle=True），并告诉它启动两个工作人员从磁盘加载数据。

将DataLoader提供的批次可视化是一个好的做法：

import matplotlib.pyplot as plt
import numpy as np

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))

# get some random training images
dataiter = iter(trainloader)
images, labels = next(dataiter)

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

introyt1 教程

Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
 ship   car horse  ship

运行上面的单元格应该会显示一条包含四幅图像和每个图像的正确标签的条带。

训练您的 PyTorch 模型

从17:10开始，跟随视频进行。

让我们把所有的部分放在一起，训练一个模型：

#%matplotlib inline

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torchvision
import torchvision.transforms as transforms

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

首先，我们需要训练和测试数据集。如果还没有，请运行下面的单元格以确保数据集已下载。（可能需要一分钟。）

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
                                         shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

Files already downloaded and verified
Files already downloaded and verified

我们将对来自DataLoader的输出运行检查：

import matplotlib.pyplot as plt
import numpy as np

# functions to show an image

def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))

# get some random training images
dataiter = iter(trainloader)
images, labels = next(dataiter)

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

introyt1 教程

cat   cat  deer  frog

这是我们将要训练的模型。如果看起来很熟悉，那是因为它是 LeNet 的一个变种-在本视频中之前讨论过-适用于 3 色图像。

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

net = Net()

我们需要的最后一些要素是损失函数和优化器：

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

损失函数，正如在本视频中之前讨论的那样，是模型预测与理想输出之间的差距的度量。交叉熵损失是我们这种分类模型的典型损失函数。

优化器是推动学习的关键。在这里，我们创建了一个实现随机梯度下降的优化器，这是更直接的优化算法之一。除了算法的参数，如学习率（lr）和动量，我们还传入net.parameters()，这是模型中所有学习权重的集合-这是优化器调整的内容。

最后，所有这些都被组装到训练循环中。继续运行此单元格，因为执行可能需要几分钟。

for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs
        inputs, labels = data

        # zero the parameter gradients
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

[1,  2000] loss: 2.195
[1,  4000] loss: 1.876
[1,  6000] loss: 1.655
[1,  8000] loss: 1.576
[1, 10000] loss: 1.519
[1, 12000] loss: 1.466
[2,  2000] loss: 1.421
[2,  4000] loss: 1.376
[2,  6000] loss: 1.336
[2,  8000] loss: 1.335
[2, 10000] loss: 1.326
[2, 12000] loss: 1.270
Finished Training

在这里，我们只进行2 个训练周期（第 1 行）-也就是说，对训练数据集进行两次遍历。每次遍历都有一个内部循环，遍历训练数据（第 4 行），提供经过转换的输入图像的批次和它们的正确标签。

将梯度归零（第 9 行）是一个重要的步骤。梯度在一个批次中累积；如果我们不为每个批次重置它们，它们将继续累积，这将提供不正确的梯度值，使学习变得不可能。

在第 12 行，我们要求模型对这个批次进行预测。在接下来的一行（第 13 行），我们计算损失-outputs（模型预测）和labels（正确输出）之间的差异。

在第 14 行，我们进行backward()传递，并计算将指导学习的梯度。

在第 15 行，优化器执行一个学习步骤-它使用backward()调用的梯度来推动学习权重朝着它认为会减少损失的方向。

循环的其余部分对 epoch 数进行了一些轻量级的报告，已完成的训练实例数量，以及训练循环中收集的损失是多少。

当您运行上面的单元格时，您应该会看到类似于这样的内容：

[1,  2000]  loss:  2.235
[1,  4000]  loss:  1.940
[1,  6000]  loss:  1.713
[1,  8000]  loss:  1.573
[1,  10000]  loss:  1.507
[1,  12000]  loss:  1.442
[2,  2000]  loss:  1.378
[2,  4000]  loss:  1.364
[2,  6000]  loss:  1.349
[2,  8000]  loss:  1.319
[2,  10000]  loss:  1.284
[2,  12000]  loss:  1.267
Finished  Training

请注意，损失是单调递减的，表明我们的模型在训练数据集上继续改善其性能。

作为最后一步，我们应该检查模型是否实际上正在进行通用学习，而不仅仅是“记忆”数据集。这被称为过拟合，通常表明数据集太小（没有足够的示例进行通用学习），或者模型具有比正确建模数据集所需的学习参数更多。

这就是数据集被分为训练和测试子集的原因 - 为了测试模型的普遍性，我们要求它对其未经训练的数据进行预测：

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d  %%' % (
    100 * correct / total))

Accuracy of the network on the 10000 test images: 54 %

如果您跟随进行，您应该看到模型在这一点上大约有 50%的准确率。这并不是最先进的，但比我们从随机输出中期望的 10%的准确率要好得多。这表明模型确实发生了一些通用学习。

脚本的总运行时间：（1 分钟 54.089 秒）

下载 Python 源代码：introyt1_tutorial.py

下载 Jupyter 笔记本：introyt1_tutorial.ipynb

Sphinx-Gallery 生成的画廊

PyTorch 张量介绍

原文：pytorch.org/tutorials/beginner/introyt/tensors_deeper_tutorial.html

译者：飞龙

协议：CC BY-NC-SA 4.0

注意

点击这里下载完整的示例代码

介绍 || 张量 || 自动求导 || 构建模型 || TensorBoard 支持 || 训练模型 || 模型理解

请跟随下面的视频或YouTube。

www.youtube.com/embed/r7QDUPb2dCM

张量是 PyTorch 中的中心数据抽象。这个交互式笔记本提供了对torch.Tensor类的深入介绍。

首先，让我们导入 PyTorch 模块。我们还将添加 Python 的 math 模块以便于一些示例。

import torch
import math

创建张量

创建张量的最简单方法是使用torch.empty()调用：

x = torch.empty(3, 4)
print(type(x))
print(x)

<class 'torch.Tensor'>
tensor([[6.0864e-06, 0.0000e+00, 1.9431e-19, 1.1024e+24],
        [8.8221e-04, 0.0000e+00, 3.9172e-05, 0.0000e+00],
        [1.1978e-35, 0.0000e+00, 7.7463e-37, 0.0000e+00]])

让我们解开刚才做的事情：

我们使用torch模块附加的众多工厂方法之一创建了一个张量。
张量本身是二维的，有 3 行和 4 列。
返回对象的类型是torch.Tensor，它是torch.FloatTensor的别名；默认情况下，PyTorch 张量由 32 位浮点数填充。（有关数据类型的更多信息请参见下文。）
打印张量时，您可能会看到一些看起来随机的值。torch.empty()调用为张量分配内存，但不会用任何值初始化它 - 所以您看到的是在分配时内存中的内容。

关于张量及其维度和术语的简要说明：

有时您会看到一个称为向量的一维张量。
同样，一个二维张量通常被称为矩阵。
超过两个维度的任何内容通常都被称为张量。

往往您会希望用某个值初始化张量。常见情况是全零、全一或随机值，torch模块为所有这些情况提供了工厂方法：

zeros = torch.zeros(2, 3)
print(zeros)

ones = torch.ones(2, 3)
print(ones)

torch.manual_seed(1729)
random = torch.rand(2, 3)
print(random)

tensor([[0., 0., 0.],
        [0., 0., 0.]])
tensor([[1., 1., 1.],
        [1., 1., 1.]])
tensor([[0.3126, 0.3791, 0.3087],
        [0.0736, 0.4216, 0.0691]])

工厂方法都只是做您期望的事情 - 我们有一个全是零的张量，另一个全是一的张量，还有一个介于 0 和 1 之间的随机值的张量。

随机张量和种子

说到随机张量，您是否注意到在其之前立即调用了torch.manual_seed()？使用随机值初始化张量，例如模型的学习权重，是常见的，但有时 - 尤其是在研究环境中 - 您会希望确保结果的可重现性。手动设置随机数生成器的种子是实现这一点的方法。让我们更仔细地看一下：

torch.manual_seed(1729)
random1 = torch.rand(2, 3)
print(random1)

random2 = torch.rand(2, 3)
print(random2)

torch.manual_seed(1729)
random3 = torch.rand(2, 3)
print(random3)

random4 = torch.rand(2, 3)
print(random4)

tensor([[0.3126, 0.3791, 0.3087],
        [0.0736, 0.4216, 0.0691]])
tensor([[0.2332, 0.4047, 0.2162],
        [0.9927, 0.4128, 0.5938]])
tensor([[0.3126, 0.3791, 0.3087],
        [0.0736, 0.4216, 0.0691]])
tensor([[0.2332, 0.4047, 0.2162],
        [0.9927, 0.4128, 0.5938]])

您应该看到random1和random3携带相同的值，random2和random4也是如此。手动设置 RNG 的种子会重置它，因此在大多数情况下，依赖随机数的相同计算应该提供相同的结果。

有关更多信息，请参阅PyTorch 关于可重现性的文档。

张量形状

通常，当您对两个或更多张量执行操作时，它们需要具有相同的形状 - 即，具有相同数量的维度和每个维度中相同数量的单元格。为此，我们有torch.*_like()方法：

x = torch.empty(2, 2, 3)
print(x.shape)
print(x)

empty_like_x = torch.empty_like(x)
print(empty_like_x.shape)
print(empty_like_x)

zeros_like_x = torch.zeros_like(x)
print(zeros_like_x.shape)
print(zeros_like_x)

ones_like_x = torch.ones_like(x)
print(ones_like_x.shape)
print(ones_like_x)

rand_like_x = torch.rand_like(x)
print(rand_like_x.shape)
print(rand_like_x)

torch.Size([2, 2, 3])
tensor([[[ 8.7595e-05,  0.0000e+00,  1.4013e-45],
         [ 0.0000e+00,  7.7463e-37,  0.0000e+00]],

        [[ 0.0000e+00,  0.0000e+00,  8.6286e-05],
         [ 0.0000e+00, -1.7707e+28,  4.5849e-41]]])
torch.Size([2, 2, 3])
tensor([[[ 0.0000e+00,  0.0000e+00,  1.4013e-45],
         [ 0.0000e+00,  7.7463e-37,  0.0000e+00]],

        [[ 0.0000e+00,  0.0000e+00,  8.6408e-05],
         [ 0.0000e+00, -1.7707e+28,  4.5849e-41]]])
torch.Size([2, 2, 3])
tensor([[[0., 0., 0.],
         [0., 0., 0.]],

        [[0., 0., 0.],
         [0., 0., 0.]]])
torch.Size([2, 2, 3])
tensor([[[1., 1., 1.],
         [1., 1., 1.]],

        [[1., 1., 1.],
         [1., 1., 1.]]])
torch.Size([2, 2, 3])
tensor([[[0.6128, 0.1519, 0.0453],
         [0.5035, 0.9978, 0.3884]],

        [[0.6929, 0.1703, 0.1384],
         [0.4759, 0.7481, 0.0361]]])

上面代码单元格中的第一个新内容是在张量上使用.shape属性。此属性包含张量每个维度的范围列表 - 在我们的情况下，x是一个形状为 2 x 2 x 3 的三维张量。

在下面，我们调用.empty_like()、.zeros_like()、.ones_like()和.rand_like()方法。使用.shape属性，我们可以验证每个方法返回的张量具有相同的维度和范围。

创建张量的最后一种方式是直接从 PyTorch 集合中指定其数据：

some_constants = torch.tensor([[3.1415926, 2.71828], [1.61803, 0.0072897]])
print(some_constants)

some_integers = torch.tensor((2, 3, 5, 7, 11, 13, 17, 19))
print(some_integers)

more_integers = torch.tensor(((2, 4, 6), [3, 6, 9]))
print(more_integers)

tensor([[3.1416, 2.7183],
        [1.6180, 0.0073]])
tensor([ 2,  3,  5,  7, 11, 13, 17, 19])
tensor([[2, 4, 6],
        [3, 6, 9]])

如果您已经有一个 Python 元组或列表中的数据，使用torch.tensor()是创建张量的最简单方式。如上所示，嵌套集合将导致一个多维张量。

注意

torch.tensor()会创建数据的副本。

张量数据类型

设置张量的数据类型有几种方式：

a = torch.ones((2, 3), dtype=torch.int16)
print(a)

b = torch.rand((2, 3), dtype=torch.float64) * 20.
print(b)

c = b.to(torch.int32)
print(c)

tensor([[1, 1, 1],
        [1, 1, 1]], dtype=torch.int16)
tensor([[ 0.9956,  1.4148,  5.8364],
        [11.2406, 11.2083, 11.6692]], dtype=torch.float64)
tensor([[ 0,  1,  5],
        [11, 11, 11]], dtype=torch.int32)

设置张量的基础数据类型的最简单方式是在创建时使用可选参数。在上面单元格的第一行中，我们为张量a设置了dtype=torch.int16。当我们打印a时，我们可以看到它充满了1而不是1. - Python 微妙地暗示这是一个整数类型而不是浮点数。

关于打印a的另一件事是，与我们将dtype保留为默认值(32 位浮点数)时不同，打印张量还会指定其dtype。

您可能还注意到，我们从将张量的形状指定为一系列整数参数开始，到将这些参数分组在一个元组中。这并不是严格必要的 - PyTorch 将一系列初始的、未标记的整数参数作为张量形状 - 但是当添加可选参数时，可以使您的意图更易读。

设置数据类型的另一种方式是使用.to()方法。在上面的单元格中，我们按照通常的方式创建了一个随机浮点张量b。在那之后，我们通过使用.to()方法将b转换为 32 位整数来创建c。请注意，c包含与b相同的所有值，但被截断为整数。

可用的数据类型包括：

torch.bool
torch.int8
torch.uint8
torch.int16
torch.int32
torch.int64
torch.half
torch.float
torch.double
torch.bfloat

使用 PyTorch 张量进行数学和逻辑运算

现在您已经了解了一些创建张量的方式…您可以用它们做什么？

让我们先看一下基本的算术运算，以及张量如何与简单标量交互：

ones = torch.zeros(2, 2) + 1
twos = torch.ones(2, 2) * 2
threes = (torch.ones(2, 2) * 7 - 1) / 2
fours = twos ** 2
sqrt2s = twos ** 0.5

print(ones)
print(twos)
print(threes)
print(fours)
print(sqrt2s)

tensor([[1., 1.],
        [1., 1.]])
tensor([[2., 2.],
        [2., 2.]])
tensor([[3., 3.],
        [3., 3.]])
tensor([[4., 4.],
        [4., 4.]])
tensor([[1.4142, 1.4142],
        [1.4142, 1.4142]])

正如您在上面看到的，张量和标量之间的算术运算，如加法、减法、乘法、除法和指数运算，会分布在张量的每个元素上。因为这样的操作的输出将是一个张量，您可以按照通常的运算符优先规则将它们链接在一起，就像我们创建threes的那一行一样。

两个张量之间的类似操作也会像您直觉地期望的那样：

powers2 = twos ** torch.tensor([[1, 2], [3, 4]])
print(powers2)

fives = ones + fours
print(fives)

dozens = threes * fours
print(dozens)

tensor([[ 2.,  4.],
        [ 8., 16.]])
tensor([[5., 5.],
        [5., 5.]])
tensor([[12., 12.],
        [12., 12.]])

这里需要注意的是，前一个代码单元中的所有张量的形状都是相同的。当我们尝试在形状不同的张量上执行二进制操作时会发生什么？

注意

以下单元格会抛出运行时错误。这是故意的。

a  =  torch.rand(2,  3)
b  =  torch.rand(3,  2)

print(a  *  b)

在一般情况下，您不能以这种方式操作形状不同的张量，即使在上面的单元格中，张量具有相同数量的元素。

简而言之：张量广播

注意

如果您熟悉 NumPy ndarrays 中的广播语义，您会发现这里也适用相同的规则。

与相同形状规则相悖的是张量广播。这里是一个例子：

rand = torch.rand(2, 4)
doubled = rand * (torch.ones(1, 4) * 2)

print(rand)
print(doubled)

tensor([[0.6146, 0.5999, 0.5013, 0.9397],
        [0.8656, 0.5207, 0.6865, 0.3614]])
tensor([[1.2291, 1.1998, 1.0026, 1.8793],
        [1.7312, 1.0413, 1.3730, 0.7228]])

这里的诀窍是什么？我们是如何将一个 2x4 的张量乘以一个 1x4 的张量的？

广播是一种在形状相似的张量之间执行操作的方式。在上面的例子中，一行四列的张量与两行四列的张量的每一行相乘。

这是深度学习中的一个重要操作。一个常见的例子是将学习权重的张量乘以一个批量的输入张量，将操作应用于批量中的每个实例，并返回一个形状相同的张量 - 就像我们上面的(2, 4) * (1, 4)的例子返回了一个形状为(2, 4)的张量。

广播的规则是：

每个张量必须至少有一个维度 - 不能是空张量。
比较两个张量的维度大小，从最后到第一个维度：
- 每个维度必须相等，或
- 其中一个维度必须为 1，或
- 一个张量中不存在的维度

当然，形状相同的张量是可以“广播”的，就像您之前看到的那样。

以下是遵守上述规则并允许广播的一些示例情况：

a =     torch.ones(4, 3, 2)

b = a * torch.rand(   3, 2) # 3rd & 2nd dims identical to a, dim 1 absent
print(b)

c = a * torch.rand(   3, 1) # 3rd dim = 1, 2nd dim identical to a
print(c)

d = a * torch.rand(   1, 2) # 3rd dim identical to a, 2nd dim = 1
print(d)

tensor([[[0.6493, 0.2633],
         [0.4762, 0.0548],
         [0.2024, 0.5731]],

        [[0.6493, 0.2633],
         [0.4762, 0.0548],
         [0.2024, 0.5731]],

        [[0.6493, 0.2633],
         [0.4762, 0.0548],
         [0.2024, 0.5731]],

        [[0.6493, 0.2633],
         [0.4762, 0.0548],
         [0.2024, 0.5731]]])
tensor([[[0.7191, 0.7191],
         [0.4067, 0.4067],
         [0.7301, 0.7301]],

        [[0.7191, 0.7191],
         [0.4067, 0.4067],
         [0.7301, 0.7301]],

        [[0.7191, 0.7191],
         [0.4067, 0.4067],
         [0.7301, 0.7301]],

        [[0.7191, 0.7191],
         [0.4067, 0.4067],
         [0.7301, 0.7301]]])
tensor([[[0.6276, 0.7357],
         [0.6276, 0.7357],
         [0.6276, 0.7357]],

        [[0.6276, 0.7357],
         [0.6276, 0.7357],
         [0.6276, 0.7357]],

        [[0.6276, 0.7357],
         [0.6276, 0.7357],
         [0.6276, 0.7357]],

        [[0.6276, 0.7357],
         [0.6276, 0.7357],
         [0.6276, 0.7357]]])

仔细观察上面每个张量的值：

创建b的乘法操作在a的每个“层”上进行了广播。
对于c，操作在a的每一层和行上进行了广播 - 每个 3 元素列都是相同的。
对于d，我们将其调整了一下 - 现在每个行在层和列之间都是相同的。

有关广播的更多信息，请参阅PyTorch 文档。

以下是一些尝试广播但将失败的示例：

注意

以下单元格会引发运行时错误。这是故意的。

a =     torch.ones(4, 3, 2)

b = a * torch.rand(4, 3)    # dimensions must match last-to-first

c = a * torch.rand(   2, 3) # both 3rd & 2nd dims different

d = a * torch.rand((0, ))   # can't broadcast with an empty tensor

就地更改张量

大多数张量上的二进制操作将返回第三个新张量。当我们说c = a * b（其中a和b是张量）时，新张量c将占用与其他张量不同的内存区域。

但是，有时您可能希望就地更改张量 - 例如，如果您正在进行可以丢弃中间值的逐元素计算。为此，大多数数学函数都有一个附加下划线（_）的版本，可以就地更改张量。

例如：

a = torch.tensor([0, math.pi / 4, math.pi / 2, 3 * math.pi / 4])
print('a:')
print(a)
print(torch.sin(a))   # this operation creates a new tensor in memory
print(a)              # a has not changed

b = torch.tensor([0, math.pi / 4, math.pi / 2, 3 * math.pi / 4])
print('\nb:')
print(b)
print(torch.sin_(b))  # note the underscore
print(b)              # b has changed

a:
tensor([0.0000, 0.7854, 1.5708, 2.3562])
tensor([0.0000, 0.7071, 1.0000, 0.7071])
tensor([0.0000, 0.7854, 1.5708, 2.3562])

b:
tensor([0.0000, 0.7854, 1.5708, 2.3562])
tensor([0.0000, 0.7071, 1.0000, 0.7071])
tensor([0.0000, 0.7071, 1.0000, 0.7071])

对于算术操作，有类似的函数行为：

a = torch.ones(2, 2)
b = torch.rand(2, 2)

print('Before:')
print(a)
print(b)
print('\nAfter adding:')
print(a.add_(b))
print(a)
print(b)
print('\nAfter multiplying')
print(b.mul_(b))
print(b)

Before:
tensor([[1., 1.],
        [1., 1.]])
tensor([[0.3788, 0.4567],
        [0.0649, 0.6677]])

After adding:
tensor([[1.3788, 1.4567],
        [1.0649, 1.6677]])
tensor([[1.3788, 1.4567],
        [1.0649, 1.6677]])
tensor([[0.3788, 0.4567],
        [0.0649, 0.6677]])

After multiplying
tensor([[0.1435, 0.2086],
        [0.0042, 0.4459]])
tensor([[0.1435, 0.2086],
        [0.0042, 0.4459]])

请注意，这些就地算术函数是torch.Tensor对象上的方法，而不像许多其他函数（例如torch.sin()）附加到torch模块。正如您从a.add_(b)中看到的那样，调用张量是在原地更改的。

还有另一种选项，可以将计算结果放入现有的分配张量中。我们迄今为止看到的许多方法和函数 - 包括创建方法！ - 都有一个out参数，让您指定一个张量来接收输出。如果out张量具有正确的形状和dtype，则可以在不进行新的内存分配的情况下完成：

a = torch.rand(2, 2)
b = torch.rand(2, 2)
c = torch.zeros(2, 2)
old_id = id(c)

print(c)
d = torch.matmul(a, b, out=c)
print(c)                # contents of c have changed

assert c is d           # test c & d are same object, not just containing equal values
assert id(c) == old_id  # make sure that our new c is the same object as the old one

torch.rand(2, 2, out=c) # works for creation too!
print(c)                # c has changed again
assert id(c) == old_id  # still the same object!

tensor([[0., 0.],
        [0., 0.]])
tensor([[0.3653, 0.8699],
        [0.2364, 0.3604]])
tensor([[0.0776, 0.4004],
        [0.9877, 0.0352]])

复制张量

与 Python 中的任何对象一样，将张量分配给变量会使变量成为张量的标签，而不是复制它。例如：

a = torch.ones(2, 2)
b = a

a[0][1] = 561  # we change a...
print(b)       # ...and b is also altered

tensor([[  1., 561.],
        [  1.,   1.]])

但是如果您想要一个单独的数据副本进行操作呢？clone()方法就是为您准备的：

a = torch.ones(2, 2)
b = a.clone()

assert b is not a      # different objects in memory...
print(torch.eq(a, b))  # ...but still with the same contents!

a[0][1] = 561          # a changes...
print(b)               # ...but b is still all ones

tensor([[True, True],
        [True, True]])
tensor([[1., 1.],
        [1., 1.]])

**在使用clone()时有一件重要的事情需要注意。**如果您的源张量启用了自动求导，那么克隆张量也会启用。**这将在自动求导的视频中更深入地介绍，但如果您想要简要了解详情，请继续阅读。

在许多情况下，这可能是您想要的。例如，如果您的模型在其forward()方法中具有多个计算路径，并且原始张量和其克隆都对模型的输出有贡献，那么为了启用模型学习，您希望为两个张量启用自动求导。如果您的源张量已启用自动求导（如果它是一组学习权重或从涉及权重的计算派生而来，则通常会启用），那么您将获得所需的结果。

另一方面，如果您进行的计算既不需要原始张量也不需要其克隆跟踪梯度，那么只要源张量关闭了自动求导，您就可以继续进行。

然而，还有第三种情况: 想象一下，你正在模型的forward()函数中执行计算，其中默认情况下为所有内容打开梯度，但你想要在中间提取一些值以生成一些指标。在这种情况下，你不希望克隆源张量跟踪梯度 - 关闭自动求导历史记录跟踪可以提高性能。为此，你可以在源张量上使用.detach()方法：

a = torch.rand(2, 2, requires_grad=True) # turn on autograd
print(a)

b = a.clone()
print(b)

c = a.detach().clone()
print(c)

print(a)

tensor([[0.0905, 0.4485],
        [0.8740, 0.2526]], requires_grad=True)
tensor([[0.0905, 0.4485],
        [0.8740, 0.2526]], grad_fn=<CloneBackward0>)
tensor([[0.0905, 0.4485],
        [0.8740, 0.2526]])
tensor([[0.0905, 0.4485],
        [0.8740, 0.2526]], requires_grad=True)

这里发生了什么？

我们使用requires_grad=True创建a。我们还没有涵盖这个可选参数，但在自动求导单元中会讨论。
当我们打印a时，它告诉我们属性requires_grad=True - 这意味着自动求导和计算历史跟踪已打开。
我们克隆a并将其标记为b。当我们打印b时，我们可以看到它正在跟踪其计算历史 - 它继承了a的自动求导设置，并添加到了计算历史中。
我们将a克隆到c，但首先调用detach()。
打印c，我们看不到计算历史，也没有requires_grad=True。

detach()方法将张量与其计算历史分离。它表示，“接下来的操作就好像自动求导已关闭一样。” 它在不更改a的情况下执行此操作 - 当我们最后再次打印a时，你会看到它保留了requires_grad=True属性。

转移到 GPU

PyTorch 的一个主要优势是其在 CUDA 兼容的 Nvidia GPU 上的强大加速。（“CUDA”代表Compute Unified Device Architecture，这是 Nvidia 用于并行计算的平台。）到目前为止，我们所做的一切都是在 CPU 上进行的。我们如何转移到更快的硬件？

首先，我们应该检查 GPU 是否可用，使用is_available()方法。

注意

如果你没有 CUDA 兼容的 GPU 和安装了 CUDA 驱动程序，本节中的可执行单元格将不会执行任何与 GPU 相关的代码。

if torch.cuda.is_available():
    print('We have a GPU!')
else:
    print('Sorry, CPU only.')

We have a GPU!

一旦我们确定有一个或多个 GPU 可用，我们需要将数据放在 GPU 可以看到的地方。你的 CPU 在计算时使用计算机 RAM 中的数据。你的 GPU 有专用内存附加在上面。每当你想在设备上执行计算时，你必须将进行该计算所需的所有数据移动到该设备可访问的内存中。（口语上，“将数据移动到 GPU 可访问的内存”缩写为“将数据移动到 GPU”。）

有多种方法可以将数据放在目标设备上。你可以在创建时执行：

if torch.cuda.is_available():
    gpu_rand = torch.rand(2, 2, device='cuda')
    print(gpu_rand)
else:
    print('Sorry, CPU only.')

tensor([[0.3344, 0.2640],
        [0.2119, 0.0582]], device='cuda:0')

默认情况下，新张量是在 CPU 上创建的，因此我们必须在想要使用可选device参数在 GPU 上创建张量时指定。当我们打印新张量时，你可以看到 PyTorch 告诉我们它在哪个设备上（如果不在 CPU 上）。

你可以使用torch.cuda.device_count()查询 GPU 的数量。如果你有多个 GPU，你可以通过索引指定它们：device='cuda:0'，device='cuda:1'等。

作为编码实践，在所有地方使用字符串常量指定设备是相当脆弱的。在理想情况下，无论你是在 CPU 还是 GPU 硬件上，你的代码都应该表现稳健。你可以通过创建一个设备句柄来实现这一点，该句柄可以传递给你的张量，而不是一个字符串：

if torch.cuda.is_available():
    my_device = torch.device('cuda')
else:
    my_device = torch.device('cpu')
print('Device: {}'.format(my_device))

x = torch.rand(2, 2, device=my_device)
print(x)

Device: cuda
tensor([[0.0024, 0.6778],
        [0.2441, 0.6812]], device='cuda:0')

如果你有一个现有张量存在于一个设备上，你可以使用to()方法将其移动到另一个设备上。以下代码行在 CPU 上创建一个张量，并将其移动到你在前一个单元格中获取的设备句柄。

y = torch.rand(2, 2)
y = y.to(my_device)

重要的是要知道，为了进行涉及两个或更多张量的计算，所有张量必须在同一设备上。无论你是否有 GPU 设备可用，以下代码都会抛出运行时错误：

x = torch.rand(2, 2)
y = torch.rand(2, 2, device='gpu')
z = x + y  # exception will be thrown

操作张量形状

有时，你需要改变张量的形状。下面，我们将看几种常见情况以及如何处理它们。

改变维度数量

有一种情况可能需要改变维度的数量，就是向模型传递单个输入实例。PyTorch 模型通常期望输入的批量。

例如，想象一个模型处理 3 x 226 x 226 的图像 - 一个有 3 个颜色通道的 226 像素正方形。当你加载和转换它时，你会得到一个形状为(3, 226, 226)的张量。然而，你的模型期望的输入形状是(N, 3, 226, 226)，其中N是批量中图像的数量。那么如何制作一个批量为 1 的批次？

a = torch.rand(3, 226, 226)
b = a.unsqueeze(0)

print(a.shape)
print(b.shape)

torch.Size([3, 226, 226])
torch.Size([1, 3, 226, 226])

unsqueeze()方法添加一个长度为 1 的维度。unsqueeze(0)将其添加为一个新的第零维 - 现在你有一个批量为 1 的张量！

那么如果是挤压呢？我们所说的挤压是什么意思？我们利用了一个事实，即任何维度的长度为 1 不会改变张量中的元素数量。

c = torch.rand(1, 1, 1, 1, 1)
print(c)

tensor([[[[[0.2347]]]]])

继续上面的例子，假设模型的输出对于每个输入是一个 20 元素向量。那么你期望输出的形状是(N, 20)，其中N是输入批次中的实例数。这意味着对于我们的单输入批次，我们将得到一个形状为(1, 20)的输出。

如果你想对这个输出进行一些非批量计算 - 比如只期望一个 20 元素的向量，怎么办？

a = torch.rand(1, 20)
print(a.shape)
print(a)

b = a.squeeze(0)
print(b.shape)
print(b)

c = torch.rand(2, 2)
print(c.shape)

d = c.squeeze(0)
print(d.shape)

torch.Size([1, 20])
tensor([[0.1899, 0.4067, 0.1519, 0.1506, 0.9585, 0.7756, 0.8973, 0.4929, 0.2367,
         0.8194, 0.4509, 0.2690, 0.8381, 0.8207, 0.6818, 0.5057, 0.9335, 0.9769,
         0.2792, 0.3277]])
torch.Size([20])
tensor([0.1899, 0.4067, 0.1519, 0.1506, 0.9585, 0.7756, 0.8973, 0.4929, 0.2367,
        0.8194, 0.4509, 0.2690, 0.8381, 0.8207, 0.6818, 0.5057, 0.9335, 0.9769,
        0.2792, 0.3277])
torch.Size([2, 2])
torch.Size([2, 2])

从形状可以看出，我们的二维张量现在是一维的，如果你仔细看上面单元格的输出，你会发现打印a会显示一个“额外”的方括号[]，因为有一个额外的维度。

你只能squeeze()长度为 1 的维度。看上面我们尝试在c中挤压一个大小为 2 的维度，最终得到的形状与开始时相同。调用squeeze()和unsqueeze()只能作用于长度为 1 的维度，因为否则会改变张量中的元素数量。

另一个可能使用unsqueeze()的地方是为了简化广播。回想一下我们之前的代码示例：

a = torch.ones(4, 3, 2)

c = a * torch.rand(   3, 1) # 3rd dim = 1, 2nd dim identical to a
print(c)

这样做的净效果是在维度 0 和 2 上广播操作，导致随机的 3 x 1 张量与a中的每个 3 元素列进行逐元素相乘。

如果随机向量只是一个 3 元素向量怎么办？我们将失去进行广播的能力，因为最终的维度不会根据广播规则匹配。unsqueeze()来拯救：

a = torch.ones(4, 3, 2)
b = torch.rand(   3)     # trying to multiply a * b will give a runtime error
c = b.unsqueeze(1)       # change to a 2-dimensional tensor, adding new dim at the end
print(c.shape)
print(a * c)             # broadcasting works again!

torch.Size([3, 1])
tensor([[[0.1891, 0.1891],
         [0.3952, 0.3952],
         [0.9176, 0.9176]],

        [[0.1891, 0.1891],
         [0.3952, 0.3952],
         [0.9176, 0.9176]],

        [[0.1891, 0.1891],
         [0.3952, 0.3952],
         [0.9176, 0.9176]],

        [[0.1891, 0.1891],
         [0.3952, 0.3952],
         [0.9176, 0.9176]]])

squeeze()和unsqueeze()方法也有原地版本，squeeze_()和unsqueeze_()：

batch_me = torch.rand(3, 226, 226)
print(batch_me.shape)
batch_me.unsqueeze_(0)
print(batch_me.shape)

torch.Size([3, 226, 226])
torch.Size([1, 3, 226, 226])

有时候你会想要更彻底地改变张量的形状，同时仍保留元素数量和内容。一个这种情况是在模型的卷积层和线性层之间的接口处 - 这在图像分类模型中很常见。卷积核会产生一个形状为特征 x 宽 x 高的输出张量，但接下来的线性层期望一个一维输入。reshape()会为你做这个，只要你请求的维度产生的元素数量与输入张量相同即可：

output3d = torch.rand(6, 20, 20)
print(output3d.shape)

input1d = output3d.reshape(6 * 20 * 20)
print(input1d.shape)

# can also call it as a method on the torch module:
print(torch.reshape(output3d, (6 * 20 * 20,)).shape)

torch.Size([6, 20, 20])
torch.Size([2400])
torch.Size([2400])

注意

上面单元格最后一行的(6 * 20 * 20,)参数是因为 PyTorch 在指定张量形状时期望一个元组 - 但当形状是方法的第一个参数时，它允许我们欺骗并只使用一系列整数。在这里，我们必须添加括号和逗号来说服方法，让它相信这实际上是一个单元素元组。

在可以的情况下，reshape()会返回一个视图，即一个查看相同底层内存区域的独立张量对象以进行更改。*这很重要：*这意味着对源张量进行的任何更改都会反映在该张量的视图中，除非你使用clone()。

在这个介绍范围之外，reshape()有时必须返回一个携带数据副本的张量。更多信息请参阅文档。

NumPy 桥接

在上面关于广播的部分中提到，PyTorch 的广播语义与 NumPy 的兼容 - 但 PyTorch 和 NumPy 之间的关系甚至比这更深。

如果您有现有的 ML 或科学代码，并且数据存储在 NumPy 的 ndarrays 中，您可能希望将相同的数据表示为 PyTorch 张量，无论是为了利用 PyTorch 的 GPU 加速，还是为了利用其构建 ML 模型的高效抽象。在 ndarrays 和 PyTorch 张量之间轻松切换：

import numpy as np

numpy_array = np.ones((2, 3))
print(numpy_array)

pytorch_tensor = torch.from_numpy(numpy_array)
print(pytorch_tensor)

[[1\. 1\. 1.]
 [1\. 1\. 1.]]
tensor([[1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)

PyTorch 创建一个与 NumPy 数组形状相同且包含相同数据的张量，甚至保留 NumPy 的默认 64 位浮点数据类型。

转换也可以同样轻松地进行另一种方式：

pytorch_rand = torch.rand(2, 3)
print(pytorch_rand)

numpy_rand = pytorch_rand.numpy()
print(numpy_rand)

tensor([[0.8716, 0.2459, 0.3499],
        [0.2853, 0.9091, 0.5695]])
[[0.87163675 0.2458961  0.34993553]
 [0.2853077  0.90905803 0.5695162 ]]

重要的是要知道，这些转换后的对象使用相同的底层内存作为它们的源对象，这意味着对一个对象的更改会反映在另一个对象中：

numpy_array[1, 1] = 23
print(pytorch_tensor)

pytorch_rand[1, 1] = 17
print(numpy_rand)

tensor([[ 1.,  1.,  1.],
        [ 1., 23.,  1.]], dtype=torch.float64)
[[ 0.87163675  0.2458961   0.34993553]
 [ 0.2853077  17\.          0.5695162 ]]

脚本的总运行时间：（0 分钟 0.294 秒）

下载 Python 源代码：tensors_deeper_tutorial.py

下载 Jupyter 笔记本：tensors_deeper_tutorial.ipynb

由 Sphinx-Gallery 生成的图库

自动微分的基础知识

原文：pytorch.org/tutorials/beginner/introyt/autogradyt_tutorial.html

译者：飞龙

协议：CC BY-NC-SA 4.0

注意

点击这里下载完整的示例代码

介绍 || 张量 || 自动微分 || 构建模型 || TensorBoard 支持 || 训练模型 || 模型理解

请跟随下面的视频或在youtube观看。

www.youtube.com/embed/M0fX15_-xrY

PyTorch 的Autograd功能是 PyTorch 灵活和快速构建机器学习项目的一部分。它允许快速且轻松地计算复杂计算中的多个偏导数（也称为梯度）。这个操作对基于反向传播的神经网络学习至关重要。

自动微分的强大之处在于它在运行时动态跟踪您的计算，这意味着如果您的模型具有决策分支，或者循环的长度直到运行时才知道，计算仍将被正确跟踪，并且您将获得正确的梯度来推动学习。这与您的模型是在 Python 中构建的事实结合在一起，比依赖于更严格结构化模型的静态分析来计算梯度的框架提供了更灵活的选择。

我们为什么需要自动微分？

机器学习模型是一个函数，具有输入和输出。在这里讨论中，我们将输入视为一个i维向量 $\vec{x}$ ，其中元素为 $x_{i}$ 。然后我们可以将模型M表示为输入的矢量值函数： $\vec{y} = \vec{M}(\vec{x})$ 。（我们将 M 的输出值视为矢量，因为一般来说，模型可能具有任意数量的输出。）

由于我们将主要讨论自动微分在训练的上下文中，我们感兴趣的输出将是模型的损失。损失函数 L( $\vec{y}$ ) = L( $\vec{M}$ ( $\vec{x}$ ))是模型输出的单值标量函数。这个函数表达了我们的模型预测与特定输入的理想输出相差多远。注意：在此之后，我们经常会省略向量符号，只要在上下文中清楚即可 - 例如， $y$ 而不是 $\vec y$ 。

在训练模型时，我们希望最小化损失。在理想情况下，对于一个完美的模型，这意味着调整其学习权重 - 即函数的可调参数 - 使得所有输入的损失为零。在现实世界中，这意味着一个迭代的过程，微调学习权重，直到我们看到我们对各种输入获得了可接受的损失。

我们如何决定在多远和哪个方向微调权重？我们希望最小化损失，这意味着使其对输入的一阶导数等于 0： $\frac{\partial L}{\partial x} = 0$ 。

然而，请记住，损失并不是直接从输入导出的，而是模型输出的函数（这是输入的函数）， $\frac{\partial L}{\partial x}$ = $\frac{\partial {L({\vec y})}}{\partial x}$ 。根据微分计算的链式法则，我们有 $\frac{\partial {L({\vec y})}}{\partial x}$ = $\frac{\partial L}{\partial y}\frac{\partial y}{\partial x}$ = $\frac{\partial L}{\partial y}\frac{\partial M(x)}{\partial x}$ 。

$\frac{\partial M(x)}{\partial x}$ 是复杂的地方。如果我们再次使用链式法则展开表达式，模型输出相对于输入的偏导数将涉及每个乘以学习权重、每个激活函数和模型中的每个其他数学变换的许多局部偏导数。每个这样的局部偏导数的完整表达式是通过计算图中以我们试图测量梯度的变量结尾的每条可能路径的局部梯度的乘积之和。

特别是，我们对学习权重上的梯度感兴趣 - 它们告诉我们改变每个权重的方向以使损失函数更接近零。

由于这种局部导数的数量（每个对应于模型计算图中的一个单独路径）往往会随着神经网络的深度呈指数增长，因此计算它们的复杂性也会增加。这就是自动微分的作用：它跟踪每次计算的历史。您 PyTorch 模型中的每个计算张量都携带其输入张量的历史记录以及用于创建它的函数。结合 PyTorch 函数旨在作用于张量的事实，每个函数都有一个用于计算自己导数的内置实现，这极大地加速了用于学习的局部导数的计算。

一个简单的例子

这是很多理论 - 但在实践中使用自动微分是什么样子呢？

让我们从一个简单的例子开始。首先，我们将进行一些导入，以便让我们绘制我们的结果：

# %matplotlib inline

import torch

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import math

接下来，我们将创建一个输入张量，其中包含区间 $2{\pi}]$ 上均匀间隔的值，并指定requires_grad=True。（像大多数创建张量的函数一样，torch.linspace()接受一个可选的requires_grad选项。）设置此标志意味着在接下来的每次计算中，autograd 将在该计算的输出张量中累积计算的历史。

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
print(a)

tensor([0.0000, 0.2618, 0.5236, 0.7854, 1.0472, 1.3090, 1.5708, 1.8326, 2.0944,
        2.3562, 2.6180, 2.8798, 3.1416, 3.4034, 3.6652, 3.9270, 4.1888, 4.4506,
        4.7124, 4.9742, 5.2360, 5.4978, 5.7596, 6.0214, 6.2832],
       requires_grad=True)

接下来，我们将进行计算，并以输入为单位绘制其输出：

b = torch.sin(a)
plt.plot(a.detach(), b.detach())

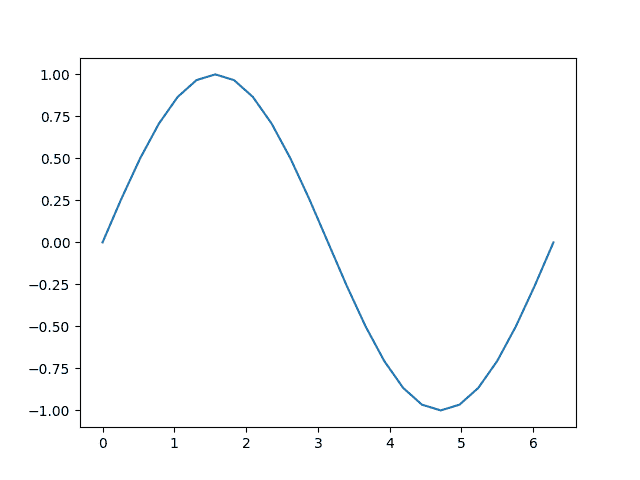
autogradyt tutorial

[<matplotlib.lines.Line2D object at 0x7f7f4ccf6f50>]

让我们更仔细地看看张量b。当我们打印它时，我们看到一个指示它正在跟踪其计算历史的指示器：

print(b)

tensor([ 0.0000e+00,  2.5882e-01,  5.0000e-01,  7.0711e-01,  8.6603e-01,
         9.6593e-01,  1.0000e+00,  9.6593e-01,  8.6603e-01,  7.0711e-01,
         5.0000e-01,  2.5882e-01, -8.7423e-08, -2.5882e-01, -5.0000e-01,
        -7.0711e-01, -8.6603e-01, -9.6593e-01, -1.0000e+00, -9.6593e-01,
        -8.6603e-01, -7.0711e-01, -5.0000e-01, -2.5882e-01,  1.7485e-07],
       grad_fn=<SinBackward0>)

这个grad_fn给了我们一个提示，即当我们执行反向传播步骤并计算梯度时，我们需要计算所有这个张量的输入的 $\sin(x)$ 的导数。

让我们进行更多的计算：

c = 2 * b
print(c)

d = c + 1
print(d)

tensor([ 0.0000e+00,  5.1764e-01,  1.0000e+00,  1.4142e+00,  1.7321e+00,
         1.9319e+00,  2.0000e+00,  1.9319e+00,  1.7321e+00,  1.4142e+00,
         1.0000e+00,  5.1764e-01, -1.7485e-07, -5.1764e-01, -1.0000e+00,
        -1.4142e+00, -1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00,
        -1.7321e+00, -1.4142e+00, -1.0000e+00, -5.1764e-01,  3.4969e-07],
       grad_fn=<MulBackward0>)
tensor([ 1.0000e+00,  1.5176e+00,  2.0000e+00,  2.4142e+00,  2.7321e+00,
         2.9319e+00,  3.0000e+00,  2.9319e+00,  2.7321e+00,  2.4142e+00,
         2.0000e+00,  1.5176e+00,  1.0000e+00,  4.8236e-01, -3.5763e-07,
        -4.1421e-01, -7.3205e-01, -9.3185e-01, -1.0000e+00, -9.3185e-01,
        -7.3205e-01, -4.1421e-01,  4.7684e-07,  4.8236e-01,  1.0000e+00],
       grad_fn=<AddBackward0>)

最后，让我们计算一个单元素输出。当您在没有参数的张量上调用.backward()时，它期望调用张量仅包含一个元素，就像在计算损失函数时一样。

out = d.sum()
print(out)

tensor(25., grad_fn=<SumBackward0>)

我们的张量中存储的每个grad_fn都允许您通过其next_functions属性一直回溯到其输入。我们可以看到，深入研究d的这个属性会显示出所有先前张量的梯度函数。请注意，a.grad_fn报告为None，表示这是一个没有自己历史记录的函数的输入。

print('d:')
print(d.grad_fn)
print(d.grad_fn.next_functions)
print(d.grad_fn.next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions[0][0].next_functions)
print('\nc:')
print(c.grad_fn)
print('\nb:')
print(b.grad_fn)
print('\na:')
print(a.grad_fn)

d:
<AddBackward0 object at 0x7f7f4ccf6ef0>
((<MulBackward0 object at 0x7f7f2c9c6650>, 0), (None, 0))
((<SinBackward0 object at 0x7f7f4ccf6ef0>, 0), (None, 0))
((<AccumulateGrad object at 0x7f7f2c9c6650>, 0),)
()

c:
<MulBackward0 object at 0x7f7f4ccf6ef0>

b:
<SinBackward0 object at 0x7f7f4ccf6ef0>

a:
None

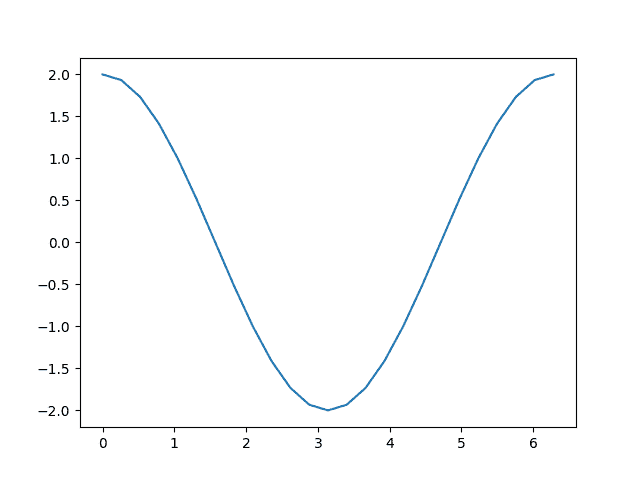
有了所有这些机制，我们如何得到导数？您在输出上调用backward()方法，并检查输入的grad属性以检查梯度：

out.backward()
print(a.grad)
plt.plot(a.detach(), a.grad.detach())

autogradyt tutorial

tensor([ 2.0000e+00,  1.9319e+00,  1.7321e+00,  1.4142e+00,  1.0000e+00,
         5.1764e-01, -8.7423e-08, -5.1764e-01, -1.0000e+00, -1.4142e+00,
        -1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00, -1.7321e+00,
        -1.4142e+00, -1.0000e+00, -5.1764e-01,  2.3850e-08,  5.1764e-01,
         1.0000e+00,  1.4142e+00,  1.7321e+00,  1.9319e+00,  2.0000e+00])

[<matplotlib.lines.Line2D object at 0x7f7f4cd6aa40>]

回顾我们走过的计算步骤：

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
b = torch.sin(a)
c = 2 * b
d = c + 1
out = d.sum()

添加一个常数，就像我们计算d时所做的那样，不会改变导数。这留下了 $\sin(a)$ ，其导数应该是 $\cos(a)$ 。从上面的图中可以看到，这正是我们看到的。

请注意，只有计算的叶节点的梯度被计算。例如，如果您尝试print(c.grad)，您会得到None。在这个简单的例子中，只有输入是叶节点，因此只有它的梯度被计算。

训练中的自动微分

我们已经简要了解了自动求导的工作原理，但是当它用于其预期目的时会是什么样子呢？让我们定义一个小模型，并检查在单个训练批次后它是如何变化的。首先，定义一些常量，我们的模型，以及一些输入和输出的替代品：

BATCH_SIZE = 16
DIM_IN = 1000
HIDDEN_SIZE = 100
DIM_OUT = 10

class TinyModel(torch.nn.Module):

    def __init__(self):
        super(TinyModel, self).__init__()

        self.layer1 = torch.nn.Linear(1000, 100)
        self.relu = torch.nn.ReLU()
        self.layer2 = torch.nn.Linear(100, 10)

    def forward(self, x):
        x = self.layer1(x)
        x = self.relu(x)
        x = self.layer2(x)
        return x

some_input = torch.randn(BATCH_SIZE, DIM_IN, requires_grad=False)
ideal_output = torch.randn(BATCH_SIZE, DIM_OUT, requires_grad=False)

model = TinyModel()

您可能会注意到，我们从未为模型的层指定requires_grad=True。在torch.nn.Module的子类中，我们假设我们希望跟踪层的权重以进行学习。

如果我们查看模型的层，我们可以检查权重的值，并验证尚未计算梯度：

print(model.layer2.weight[0][0:10]) # just a small slice
print(model.layer2.weight.grad)

tensor([ 0.0920,  0.0916,  0.0121,  0.0083, -0.0055,  0.0367,  0.0221, -0.0276,
        -0.0086,  0.0157], grad_fn=<SliceBackward0>)
None

让我们看看当我们运行一个训练批次时会发生什么变化。对于损失函数，我们将使用prediction和ideal_output之间的欧几里德距离的平方，我们将使用基本的随机梯度下降优化器。

optimizer = torch.optim.SGD(model.parameters(), lr=0.001)

prediction = model(some_input)

loss = (ideal_output - prediction).pow(2).sum()
print(loss)

tensor(211.2634, grad_fn=<SumBackward0>)

现在，让我们调用loss.backward()并看看会发生什么：

loss.backward()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])

tensor([ 0.0920,  0.0916,  0.0121,  0.0083, -0.0055,  0.0367,  0.0221, -0.0276,
        -0.0086,  0.0157], grad_fn=<SliceBackward0>)
tensor([12.8997,  2.9572,  2.3021,  1.8887,  5.0710,  7.3192,  3.5169,  2.4319,
         0.1732, -5.3835])

我们可以看到为每个学习权重计算了梯度，但是权重保持不变，因为我们还没有运行优化器。优化器负责根据计算出的梯度更新模型权重。

optimizer.step()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])

tensor([ 0.0791,  0.0886,  0.0098,  0.0064, -0.0106,  0.0293,  0.0186, -0.0300,
        -0.0088,  0.0211], grad_fn=<SliceBackward0>)
tensor([12.8997,  2.9572,  2.3021,  1.8887,  5.0710,  7.3192,  3.5169,  2.4319,
         0.1732, -5.3835])

您应该看到layer2的权重已经改变了。

关于这个过程的一个重要事项：在调用optimizer.step()之后，您需要调用optimizer.zero_grad()，否则每次运行loss.backward()时，学习权重上的梯度将会累积：

print(model.layer2.weight.grad[0][0:10])

for i in range(0, 5):
    prediction = model(some_input)
    loss = (ideal_output - prediction).pow(2).sum()
    loss.backward()

print(model.layer2.weight.grad[0][0:10])

optimizer.zero_grad(set_to_none=False)

print(model.layer2.weight.grad[0][0:10])

tensor([12.8997,  2.9572,  2.3021,  1.8887,  5.0710,  7.3192,  3.5169,  2.4319,
         0.1732, -5.3835])
tensor([ 19.2095, -15.9459,   8.3306,  11.5096,   9.5471,   0.5391,  -0.3370,
          8.6386,  -2.5141, -30.1419])
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

在运行上面的单元格后，您应该看到在多次运行loss.backward()后，大多数梯度的幅度会更大。在运行下一个训练批次之前未将梯度归零会导致梯度以这种方式增加，从而导致不正确和不可预测的学习结果。

关闭和打开自动求导

有些情况下，您需要对是否启用自动求导进行细粒度控制。根据情况，有多种方法可以实现这一点。

最简单的方法是直接在张量上更改requires_grad标志：

a = torch.ones(2, 3, requires_grad=True)
print(a)

b1 = 2 * a
print(b1)

a.requires_grad = False
b2 = 2 * a
print(b2)

tensor([[1., 1., 1.],
        [1., 1., 1.]], requires_grad=True)
tensor([[2., 2., 2.],
        [2., 2., 2.]], grad_fn=<MulBackward0>)
tensor([[2., 2., 2.],
        [2., 2., 2.]])

在上面的单元格中，我们看到b1有一个grad_fn（即跟踪的计算历史），这是我们所期望的，因为它是从打开自动求导的张量a派生出来的。当我们使用a.requires_grad = False显式关闭自动求导时，计算历史不再被跟踪，这是我们在计算b2时看到的。

如果您只需要暂时关闭自动求导，更好的方法是使用torch.no_grad()：

a = torch.ones(2, 3, requires_grad=True) * 2
b = torch.ones(2, 3, requires_grad=True) * 3

c1 = a + b
print(c1)

with torch.no_grad():
    c2 = a + b

print(c2)

c3 = a * b
print(c3)

tensor([[5., 5., 5.],
        [5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
        [5., 5., 5.]])
tensor([[6., 6., 6.],
        [6., 6., 6.]], grad_fn=<MulBackward0>)

torch.no_grad()也可以作为函数或方法装饰器使用：

def add_tensors1(x, y):
    return x + y

@torch.no_grad()
def add_tensors2(x, y):
    return x + y

a = torch.ones(2, 3, requires_grad=True) * 2
b = torch.ones(2, 3, requires_grad=True) * 3

c1 = add_tensors1(a, b)
print(c1)

c2 = add_tensors2(a, b)
print(c2)

tensor([[5., 5., 5.],
        [5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
        [5., 5., 5.]])

有一个相应的上下文管理器torch.enable_grad()，用于在自动求导尚未启用时打开自动求导。它也可以用作装饰器。

最后，您可能有一个需要跟踪梯度的张量，但您想要一个不需要的副本。为此，我们有Tensor对象的detach()方法-它创建一个与计算历史分离的张量的副本：

x = torch.rand(5, requires_grad=True)
y = x.detach()

print(x)
print(y)

tensor([0.0670, 0.3890, 0.7264, 0.3559, 0.6584], requires_grad=True)
tensor([0.0670, 0.3890, 0.7264, 0.3559, 0.6584])

当我们想要绘制一些张量时，我们在上面做了这个操作。这是因为matplotlib期望输入为 NumPy 数组，并且对于requires_grad=True的张量，PyTorch 不会启用从 PyTorch 张量到 NumPy 数组的隐式转换。制作一个分离的副本让我们可以继续前进。

自动求导和原地操作

到目前为止，在本笔记本中的每个示例中，我们都使用变量来捕获计算的中间值。自动求导需要这些中间值来执行梯度计算。*因此，在使用自动求导时，您必须小心使用原地操作。*这样做可能会破坏您在backward()调用中需要计算导数的信息。如果您尝试对需要自动求导的叶变量进行原地操作，PyTorch 甚至会阻止您，如下所示。

注意

以下代码单元格会抛出运行时错误。这是预期的。

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
torch.sin_(a)

自动求导分析器

Autograd 详细跟踪计算的每一步。这样的计算历史，结合时间信息，将成为一个方便的分析器 - autograd 已经内置了这个功能。这里是一个快速示例用法：

device = torch.device('cpu')
run_on_gpu = False
if torch.cuda.is_available():
    device = torch.device('cuda')
    run_on_gpu = True

x = torch.randn(2, 3, requires_grad=True)
y = torch.rand(2, 3, requires_grad=True)
z = torch.ones(2, 3, requires_grad=True)

with torch.autograd.profiler.profile(use_cuda=run_on_gpu) as prf:
    for _ in range(1000):
        z = (z / x) * y

print(prf.key_averages().table(sort_by='self_cpu_time_total'))

-------------------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------
                     Name    Self CPU %      Self CPU   CPU total %     CPU total  CPU time avg     Self CUDA   Self CUDA %    CUDA total  CUDA time avg    # of Calls
-------------------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------
          cudaEventRecord        43.53%       8.673ms        43.53%       8.673ms       2.168us       0.000us         0.00%       0.000us       0.000us          4000
                aten::div        28.70%       5.719ms        28.70%       5.719ms       5.719us      16.108ms        50.04%      16.108ms      16.108us          1000
                aten::mul        27.69%       5.518ms        27.69%       5.518ms       5.518us      16.083ms        49.96%      16.083ms      16.083us          1000
    cudaDeviceSynchronize         0.08%      15.000us         0.08%      15.000us      15.000us       0.000us         0.00%       0.000us       0.000us             1
-------------------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------
Self CPU time total: 19.925ms
Self CUDA time total: 32.191ms

分析器还可以标记代码的各个子块，按输入张量形状拆分数据，并将数据导出为 Chrome 跟踪工具文件。有关 API 的完整详细信息，请参阅文档。

高级主题：更多 Autograd 细节和高级 API

如果你有一个具有 n 维输入和 m 维输出的函数 $\vec{y}=f(\vec{x})$ ，完整的梯度是一个矩阵，表示每个输出对每个输入的导数，称为雅可比矩阵：

$\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)$

如果你有一个第二个函数， $l=g\left(\vec{y}\right)$ ，它接受 m 维输入（即与上面输出相同维度），并返回一个标量输出，你可以将其相对于 $\vec{y}$ 的梯度表示为一个列向量， $v=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}$ - 这实际上只是一个一列雅可比矩阵。

更具体地，想象第一个函数是你的 PyTorch 模型（可能有许多输入和许多输出），第二个函数是一个损失函数（以模型的输出为输入，损失值为标量输出）。

如果我们将第一个函数的雅可比矩阵乘以第二个函数的梯度，并应用链式法则，我们得到：

$J^{T}\cdot v=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}} \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right)$

注意：你也可以使用等效的操作 $v^{T}\cdot J$ ，并得到一个行向量。

得到的列向量是第二个函数相对于第一个函数的输入的梯度 - 或者在我们的模型和损失函数的情况下，是损失相对于模型输入的梯度。

**torch.autograd是用于计算这些乘积的引擎。**这是我们在反向传播过程中累积梯度的方式。

因此，backward()调用也可以同时接受一个可选的向量输入。这个向量表示张量上的一组梯度，这些梯度将乘以其前面的 autograd 跟踪张量的雅可比矩阵。让我们尝试一个具体的例子，使用一个小向量：

x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

tensor([  299.4868,   425.4009, -1082.9885], grad_fn=<MulBackward0>)

如果我们现在尝试调用y.backward()，我们会得到一个运行时错误和一个梯度只能隐式计算为标量输出的消息。对于多维输出，autograd 希望我们提供这三个输出的梯度，以便将其乘入雅可比矩阵：

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) # stand-in for gradients
y.backward(v)

print(x.grad)

tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

（请注意，输出梯度都与 2 的幂相关 - 这是我们从重复加倍操作中期望的。）

高级 API

在 autograd 上有一个 API，它可以直接访问重要的微分矩阵和向量运算。特别是，它允许你计算特定输入的特定函数的雅可比矩阵和Hessian矩阵。（Hessian 类似于雅可比矩阵，但表达了所有偏导数的二阶导数。）它还提供了用这些矩阵进行向量乘积的方法。

让我们计算一个简单函数的雅可比矩阵，对于 2 个单元素输入进行评估：

def exp_adder(x, y):
    return 2 * x.exp() + 3 * y

inputs = (torch.rand(1), torch.rand(1)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)

(tensor([0.7212]), tensor([0.2079]))

(tensor([[4.1137]]), tensor([[3.]]))

如果仔细观察，第一个输出应该等于 $2e^x$ （因为 $e^x$ 的导数是 $e^x$ ），第二个值应该是 3。

当然，您也可以使用高阶张量来做到这一点：

inputs = (torch.rand(3), torch.rand(3)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)

(tensor([0.2080, 0.2604, 0.4415]), tensor([0.5220, 0.9867, 0.4288]))

(tensor([[2.4623, 0.0000, 0.0000],
        [0.0000, 2.5950, 0.0000],
        [0.0000, 0.0000, 3.1102]]), tensor([[3., 0., 0.],
        [0., 3., 0.],
        [0., 0., 3.]]))

torch.autograd.functional.hessian()方法的工作方式相同（假设您的函数是两次可微的），但返回所有二阶导数的矩阵。

还有一个函数可以直接计算向量-Jacobian 乘积，如果您提供向量的话：

def do_some_doubling(x):
    y = x * 2
    while y.data.norm() < 1000:
        y = y * 2
    return y

inputs = torch.randn(3)
my_gradients = torch.tensor([0.1, 1.0, 0.0001])
torch.autograd.functional.vjp(do_some_doubling, inputs, v=my_gradients)

(tensor([-665.7186, -866.7054,  -58.4194]), tensor([1.0240e+02, 1.0240e+03, 1.0240e-01]))

torch.autograd.functional.jvp()方法执行与vjp()相同的矩阵乘法，但操作数的顺序相反。vhp()和hvp()方法对向量-海森乘积执行相同的操作。

有关更多信息，包括有关功能 API 的性能说明，请参阅功能 API 文档

脚本的总运行时间：（0 分钟 0.706 秒）

下载 Python 源代码：autogradyt_tutorial.py

下载 Jupyter 笔记本：autogradyt_tutorial.ipynb

Sphinx-Gallery 生成的图库