Codeforces Round #842 (Div. 2) C. Elemental Decompress

news2024/11/27 6:28:20

翻译：

您将得到一个由𝑛个整数组成的数组𝑎。

找到两个排列组合𝑝长度和𝑞𝑛这样马克斯(𝑝𝑖,𝑞𝑖)=𝑎𝑖所有1≤𝑖≤𝑛或报告这样𝑝𝑞并不存在。

†一个长度为𝑛的排列是一个由𝑛个不同的整数组成的数组，从1到𝑛，顺序是任意的。例如，[2,3,1,5,4]是一个排列，但[1,2,2]不是一个排列(2在数组中出现了两次)，[1,3,4]也不是一个排列(𝑛=3，但数组中有4)。

输入

第一行包含一个整数𝑡(1≤𝑡≤104)——测试用例的数量。测试用例的描述如下。

每个测试用例的第一行包含一个整数𝑛(1≤𝑛≤2⋅105)。

每个测试用例的第二行包含𝑛整数𝑎1𝑎2,…,𝑎𝑛(1≤𝑎𝑖≤𝑛)——𝑎数组。

可以保证𝑛对所有测试用例的总和不超过2⋅105。

输出

对于每个测试用例，如果不存在满足条件的𝑝和𝑞，则输出“NO”(不带引号)。

否则，输出“YES”(不带引号)，然后输出2行。第一行应该包含𝑛整数𝑝1，𝑝2，…，𝑝𝑛，第二行应该包含𝑛整数𝑞1，𝑞2，…，𝑞𝑛。

如果有多个解决方案，则可以输出其中任何一个。

您可以在任何情况下输出“YES”和“NO”(例如，字符串“YES”，“YES”和“YES”将被识别为积极响应)。

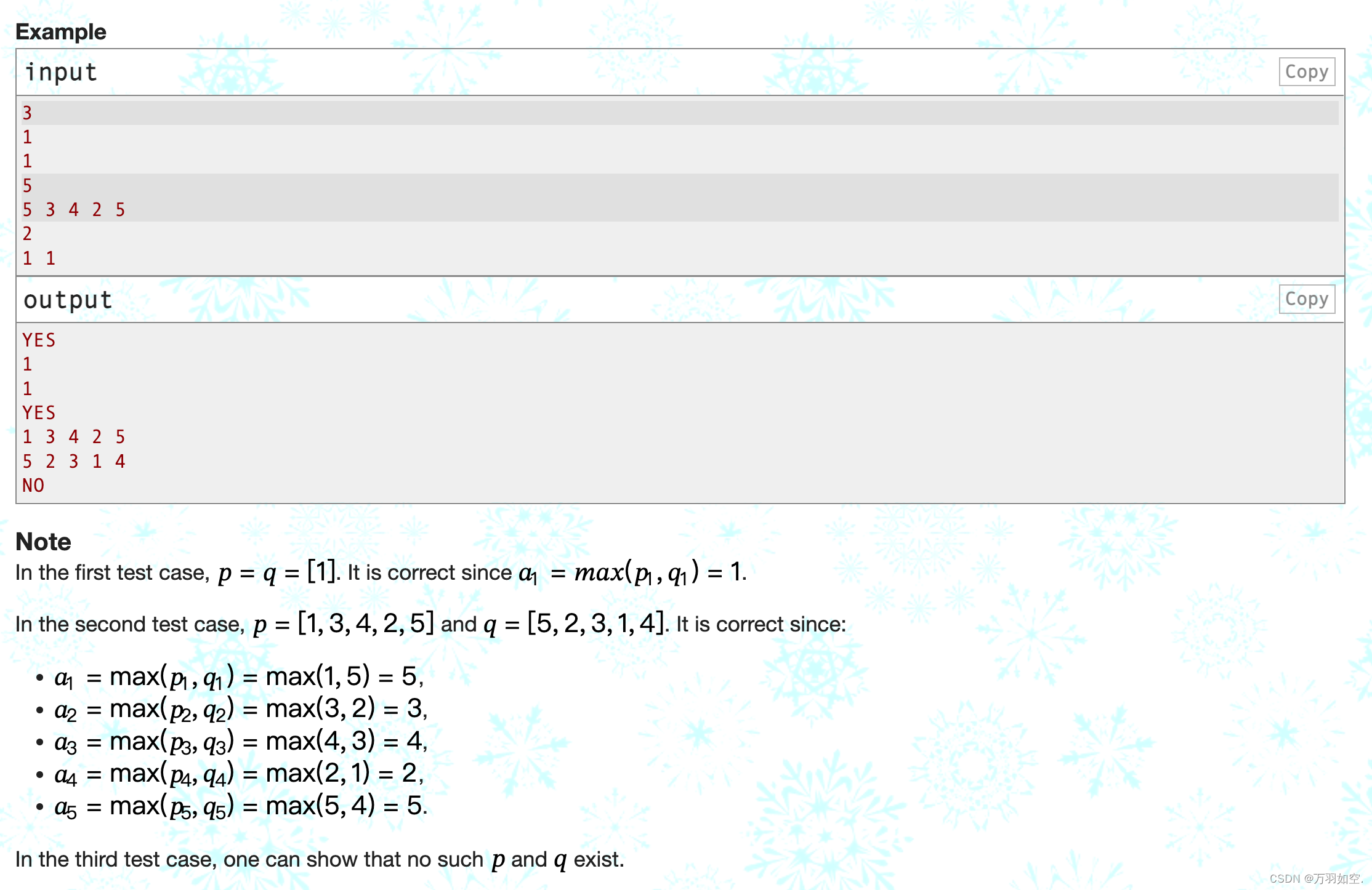
例子

inputCopy

3.

1

1

5

5 3 4 2 5

2

1

outputCopy

是的

1

1

是的

1 3 4 2 5

5 2 3 1 4

没有

请注意

在第一个测试用例中，𝑝=𝑞=[1]。这是正确的，因为𝑎1=𝑚𝑎𝑥(𝑝1，𝑞1)=1。

在第二个测试用例,𝑝=(1、3、4、2、5)和𝑞=[5,2、3、1,4]。是正确的，因为:

𝑎1 = max(𝑝1𝑞1)= max(1、5)= 5,

𝑎2 = max(𝑝2𝑞2)= max (3 2) = 3,

𝑎3 = max(𝑝3𝑞3)= max (4,3) = 4,

𝑎4 = max(𝑝4𝑞4)= max (2, 1) = 2,

𝑎5 = max(𝑝5𝑞5)= max(5 4) = 5。

在第三个测试用例中，可以显示不存在𝑝和𝑞。

思路：利用STL，然后无脑暴力，先放可以放的，无法决定的存入优先队列里面，然后没有放的也排下序，为了尽量能放下肯定先放小的，所以能放就放，最后判断一下就好了。‘

代码：

/*Looking! The blitz loop this planet to search way
 
 Only my RAILGUN can shoot it 今すぐ
 
 身体中を  光の速さで
 
 駆け巡った確かな予感
 
 掴め！ 望むものなら残さず
 
 輝ける自分らしさで
 
 信じてるよ  あの日の誓いを
 
 この瞳に光る涙それさえも  強さになるから
 
 */
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}

namespace simpler{
template<const unsigned _Mod=INT32_MAX>
class modint{
protected:
    int64_t _val;
    typedef modint<_Mod> _mint;
    friend inline _mint
    __construct(_mint&& _res,int64_t _x){
        _res._val=_x;
        return _res;
    }
    template<class _Tp>friend _mint
    __quickly_power(_mint _a,_Tp _b){
        if(_b<=0)return 1;
        _mint _res=1;
        for(;(bool)_b;_b>>=1,_a*=_a)if(_b&1)_res*=_a;
        return _res;
    }
public:
    modint():_val(0){}
    template<class _Tp>modint(_Tp _x){
        _val=((int64_t)_x%_Mod+_Mod)%_Mod;
    }
    template<class _Tp>explicit inline operator _Tp(){return (_Tp)_val;}
    
    friend _mint operator+(const _mint& _a,const _mint& _b){
        if(_a._val+_b._val>=_Mod)return __construct(_mint(),_a._val+_b._val-_Mod);
        return __construct(_mint(),_a._val+_b._val);
    }
    inline _mint& operator+=(const _mint& _b){return *this=*this+_b;}
    inline _mint& operator++(){return *this=*this+__construct(_mint(),1);}
    inline _mint& operator++(int){
        _mint _res=*this;*this=*this+__construct(_mint(),1);
        return _res;
    }//plus
    friend _mint operator-(const _mint& _a,const _mint& _b){
        if(_a._val-_b._val<0)return __construct(_mint(),_a._val-_b._val+_Mod);
        return __construct(_mint(),_a._val-_b._val);
    }
    inline _mint& operator-=(const _mint& _b){return *this=*this-_b;}
    inline _mint& operator--(){return *this=*this-__construct(_mint(),1);}
    inline _mint& operator--(int){
        _mint _res=*this;*this=*this-__construct(_mint(),1);
        return _res;
    }//minus
    friend inline _mint
    operator*(const _mint& _a,const _mint& _b){
        return __construct(_mint(),_a._val*_b._val%_Mod);
    }
    inline _mint& operator*=(const _mint& _b){return *this=*this*_b;}//multiplies
    _mint operator-(){return __construct(_mint(),_val?_Mod-_val:_val);}//negative
    friend inline _mint
    operator%(const _mint& _a,const _mint& _b){
        return __construct(_mint(),_a._val%_b._val);
    }
    inline _mint& operator%=(const _mint& _b){return *this=*this%_b;}//modulus
    
    friend inline bool
    operator==(const _mint& _a,const _mint& _b){
        return _a._val==_b._val;
    }
    friend inline bool
    operator!=(const _mint& _a,const _mint& _b){
        return _a._val!=_b._val;
    }
    friend inline bool
    operator<(const _mint& _a,const _mint& _b){
        return _a._val<_b._val;
    }
    friend inline bool
    operator>(const _mint& _a,const _mint& _b){
        return _a._val>_b._val;
    }
    friend inline bool
    operator<=(const _mint& _a,const _mint& _b){
        return _a._val<=_b._val;
    }
    friend inline bool
    operator>=(const _mint& _a,const _mint& _b){
        return _a._val>=_b._val;
    }
    
    friend inline _mint
    operator&(const _mint& _a,const _mint& _b){
        return _a._val&_b._val;
    }
    inline _mint& operator&=(const _mint& _b){return *this=*this&_b;}
    friend inline _mint
    operator|(const _mint& _a,const _mint& _b){
        return _a._val|_b._val;
    }
    inline _mint& operator|=(const _mint& _b){return *this=*this|_b;}
    friend inline _mint
    operator^(const _mint& _a,const _mint& _b){
        return _a._val^_b._val;
    }
    inline _mint& operator^=(const _mint& _b){return *this=*this^_b;}
    friend inline _mint
    operator<<(const _mint& _a,const _mint& _b){
        return _a._val<<_b._val;
    }
    inline _mint& operator<<=(const _mint& _b){return *this=*this<<_b;}
    friend inline _mint
    operator>>(const _mint& _a,const _mint& _b){
        return _a._val>>_b._val;
    }
    inline _mint& operator>>=(const _mint& _b){return *this=*this>>_b;}
    inline _mint operator~()const{return __construct(_mint(),~_val);}
    inline bool  operator!()const{return !_val;}
    
    friend inline std::istream&
    operator>>(std::istream& _is,_mint& _b){
        return _is>>_b._val;
    }
    friend inline std::ostream&
    operator<<(std::ostream& _os,const _mint& _b){
        return _os<<_b._val;
    }
    
    template<class _Tp>_mint
    power(_Tp _n)const{
        return __quickly_power(*this,_n);
    }
    inline _mint inv()const{return __quickly_power(*this,_Mod-2);}
    
    friend inline _mint
    operator/(const _mint& _a,const _mint& _b){
        return __construct(_mint(),_a._val*_b.inv()._val%_Mod);
    }
    inline _mint& operator/=(const _mint& _b){return *this=*this/_b;}
};//modint 2.0
}
using mint=simpler::modint<998244353>;
const int Maxn=2e5+5;
//definition
//mint a[Maxn];
//mint f[2][Maxn];
int n,t;
int a[200005];
struct we{
    int x,y;
}p[200005],q[200005];
int an1[200005],an2[200005];
bool cmp(we a,we b){
    return a.x<b.x;
}
bool cmp2(we a,we b){
    return a.y<b.y;
}
void wanyurukong(){
    cin>>n;
    map<int,int>ff;
    bool bj=0;
    for (int i =1; i<=n; i++) {
        cin>>a[i];
        p[i].x=-1;
        q[i].x=-1;
        an1[i]=an2[i]=-9999;
        ff[a[i]]++;
        if (ff[a[i]]>2) {
            bj=1;
        }
    }
    if (bj||ff[1]>=2) {
        printf("NO\n");return;
    }
    set<int>f1,f2;
    for (int i =1; i<=n; i++) {
        if (ff[a[i]]==1) {
            ff[a[i]]--;
            p[i].x=a[i];
            an1[i]=a[i];
            f1.insert(a[i]);
        }
        else if(ff[a[i]]==2){
            ff[a[i]]--;
            q[i].x=a[i];
            an2[i]=a[i];
            f2.insert(a[i]);
        }
        p[i].y=q[i].y=i;
    }
    priority_queue<int,vector<int>,greater<int>>d1,d2;
    for (int i =1; i<=n; i++) {
        if (!f1.count(i)) {
            d1.push(i);
        }
        if (!f2.count(i)) {
            d2.push(i);
        }
    }
    sort(p+1, p+1+n, cmp);
    sort(q+1, q+1+n, cmp);
    for (int i =1; i<=n; i++) {
        if (q[i].x==-1) {
            continue;
        }
        if (d1.top()<=q[i].x) {
            an1[q[i].y]=d1.top();
            d1.pop();
        }
//        else{
//            printf("NO\n");return;
//        }
    }
    for (int i =1; i<=n; i++) {
        if (p[i].x==-1) {
            continue;
        }
        if (d2.top()<=p[i].x) {
            an2[p[i].y]=d2.top();
            d2.pop();
        }
//        else{
//            printf("NO\n");return;
//        }
    }
//    sort(p+1, p+1+n, cmp2);
//    sort(q+1, q+1+n, cmp2);
    if (*min_element(an1+1, an1+1+n)==-9999||*min_element(an2+1, an2+1+n)==-9999) {
        printf("NO\n");return;
    }
    printf("YES\n");
    for (int i =1; i<=n; i++) {
        printf("%d ",an1[i]);
    }printf("\n");
    for (int i =1; i<=n; i++) {
        printf("%d ",an2[i]);
    }printf("\n");
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        wanyurukong();
    }
    //wanyurukong
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/143253.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Spring Boot学习篇(七)

Spring Boot学习篇(七)

Spring Boot学习篇(七) 1.thymeleaf模板引擎使用篇(一) 1.1 准备工作 1.1.1 在pom.xml中导入所需要的依赖 a thymeleaf模板引擎所需要的依赖 <!--thymeleaf模板引擎,前后端不分离的时候用 普通的html格式--> <dependency><groupId>org.springframework.…
阅读更多...
计算机网络实验---Wireshark 实验

计算机网络实验---Wireshark 实验

数据链路层 实作一/熟悉 Ethernet 帧结构 实作二/了解子网内/外通信时的 MAC 地址 实作三/掌握 ARP 解析过程 网络层 实作一 /熟悉 IP 包结构 实作二 IP 包的分段与重组 实作三 考察 TTL 事件 传输层 实作一 熟悉 TCP 和 UDP 段结构 实作二 分析 TCP 建立和释放连接 应用层 …
阅读更多...
数据结构基本介绍

数据结构基本介绍

1.what is Data Structure? A data structure is a memory used to store and organize dataIt is also used for processing, retrieving, and storing data 2. what is classification of Data Structure? 2.1 what is Linear data structure? Data structure in which…
阅读更多...
你还不懂递归么？不允许你不懂，进来折腾下自己吧

你还不懂递归么？不允许你不懂，进来折腾下自己吧

举例数组 const arr [ {id: "1175310929766055936", pid: "", name: "总裁办" },---返回空数组, {id: "1175311213774962688", pid: "", name: "行政部" },---返回空数组, {id: "1175311267684352000&qu…
阅读更多...
随想录一刷Day27——回溯算法

随想录一刷Day27——回溯算法

文章目录Day27_回溯算法13. 子集 II14. 491.递增子序列15. 全排列全排列 IIDay27_回溯算法 13. 子集 II 90. 子集 II class Solution { private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startI…
阅读更多...
[SwiftUI 开发] Widget 小组件

[SwiftUI 开发] Widget 小组件

小组件简述 小组件可以在主屏幕上实现内容展示和功能跳转。 系统会向小组件获取时间线&#xff0c;根据当前时间对时间线上的数据进行展示。点击正在展示的视觉元素可以跳转到APP内&#xff0c;实现对应的功能。 小组件是一个独立于 App 环境(即 App Extension)&#xff0c;小…
阅读更多...
谷粒学院——第二十一章、spring security详细

谷粒学院——第二十一章、spring security详细

一、Spring Security介绍 1、Spring Security简介 Spring 是非常流行和成功的 Java 应用开发框架&#xff0c;Spring Security 正是 Spring 家族中的成员。Spring Security 基于 Spring 框架&#xff0c;提供了一套 Web 应用安全性的完整解决方案。 正如你可能知道的关于安全…
阅读更多...
年度征文｜2022年「博客之星」，花落谁家？ 大家来竞猜吧

年度征文｜2022年「博客之星」，花落谁家？ 大家来竞猜吧

一年一度的「博客之星」大赛如火如荼地进行着&#xff0c;大家都忙着评分、发帖、回帖.....今天发现我在分组的排名只有40多名&#xff0c;基本上算是放弃了。但是&#xff0c;看到本文的朋友&#xff0c;还是可以帮我拉拉票的&#xff01;请点开链接给个五星评分&#xff1a; …
阅读更多...
CentOS服务器署Springboot的java项目最简单操作步骤

CentOS服务器署Springboot的java项目最简单操作步骤

CentOS服务器署Springboot的java项目最简单操作步骤 准备工作 1.首先本地有一个能跑起来正常的 java 项目的 jar 包; 2.有一个前端项目, 可以仅是一个 index.html 文件; 3.需要备案好的域名 (可选, 否则只能 ip 访问) 4.购买阿里云或者腾讯云等等任意 CentOS 服务器一个 1. 获…
阅读更多...
（机器学习深度学习常用库、框架|Pytorch篇）第（待定）节：卷积神经网络CNN中一些经典网络结构写法

（机器学习深度学习常用库、框架|Pytorch篇）第（待定）节：卷积神经网络CNN中一些经典网络结构写法

文章目录一&#xff1a;LeNet-5二&#xff1a;AlexNet三&#xff1a;VGG四&#xff1a;ResNet五&#xff1a;MobileNetV1六&#xff1a;InceptionNet一&#xff1a;LeNet-5 LeNet-5&#xff1a;LeNet-5是一个较简单的卷积神经网络。下图显示了其结构&#xff1a;输入的二维图像…
阅读更多...
ansible通过多种方法配置yum源仓库

ansible通过多种方法配置yum源仓库

目录 1.挂载本地光盘到/mnt ​2.配置yum源仓库文件通过多种方式实现 仓库1 &#xff1a;Name: RH294_BaseDescription&#xff1a; RH294 base softwareBase urt: file:///mnt/BaseOS不需要验证钦件包 GPG 签名启用此软件仓库 ​编辑仓库 2:Name: RH294_StreamDescription &…
阅读更多...
第四十二篇 nextTick

第四十二篇 nextTick

在前面封装swiper组件当中&#xff0c;通过许多种方式方法&#xff0c;其一从mounted初始化过早转到updated后出现初始化重复&#xff0c;再者通过设置key值和使用v-if控制swiper组件&#xff0c;然后通过Vue.diretive自定义指令的方式来封装swiper组件&#xff0c;那么本篇的n…
阅读更多...
排序算法之快速排序

排序算法之快速排序

目录 排序算法介绍 快速排序 算法流程 算法实现 python C 快排为什么快 算法优化 基准数优化 python C 尾递归优化 python C 排序算法介绍 《Hello算法》是GitHub上一个开源书籍&#xff0c;对新手友好&#xff0c;有大量的动态图&#xff0c;很适合算法初学者自…
阅读更多...
Struts2框架标签

Struts2框架标签

Struts2框架标签1、前言2、UI标签2.1、表单标签2.1、非表单标签3、通用标签4、例子4.1、实体类User4.2、控制器UserAction4.3、配置文件struts.xml4.4、页面users.jsp4.5、测试1、前言 Struts2有丰富的tag标签可以使用&#xff0c;即Struts2的标签库&#xff0c;如果能够灵活运…
阅读更多...
彻底理解动态规划：编辑距离

彻底理解动态规划：编辑距离

本篇的题目非常经典&#xff0c;几乎是面试必备&#xff0c;即&#xff0c;编辑距离问题&#xff0c;edit distance&#xff1b; 给定两个字符串word1以及word2&#xff0c;返回将word1转为word2需要的最少步骤&#xff0c;在每一步中你可以针对字符串word1进行以下操作&#…
阅读更多...
技术开发115

技术开发115

技术开发115 业务内容&#xff1a; 拖车用辅助脚、拖车用零件类、特殊车辆用车轴Sub。Assy产品、面向汽车产业的生产设备、面向建设机械的零部件类、面向汽车产业的检查夹具 公司简介&#xff1a; 董事长&#xff1a;佐藤安弘 资本金&#xff1a;4500万日元 员工数&#x…
阅读更多...
shell第五天练习

shell第五天练习

题目&#xff1a; 1、编写函数&#xff0c;实现打印绿色OK和红色FAILED&#xff0c;判断是否有参数&#xff0c;存在为Ok&#xff0c;不存在为FAILED 2、编写函数&#xff0c;实现判断是否无位置参数&#xff0c;如无参数&#xff0c;提示错误 3、编写函数实现两个数字做为参数…
阅读更多...
聊聊前端安全之CSRF

聊聊前端安全之CSRF

本文作者为奇舞团前端开发工程师一、什么是CSRFCSRF&#xff08;Cross Site Request Forgery&#xff0c;跨站域请求伪造&#xff09;&#xff0c;通常缩写为 CSRF。CSRF攻击是攻击者通过伪装成受信任用户向服务器发起各种请求&#xff0c;达到欺骗服务器接收并执行指令&#x…
阅读更多...
【数据结构】顺序表

【数据结构】顺序表

【本篇内容】线性表顺序表线性表线性表是n个具有相同特性的数据元素的有限序列。常见的线性表&#xff1a;顺序表、链表、栈、队列、字符串......线性表在逻辑上是线性结构&#xff0c;但是在物理结构上并一定是连续的&#xff0c;线性表在物理上存储时&#xff0c;通常是以数组…
阅读更多...
保证原子性的几种方式，你都知道吗？？？

保证原子性的几种方式，你都知道吗？？？

1. 前言 今天主要是从实战 浅谈原理的角度来说下&#xff0c;并发线程下原子性的几种处理方式&#xff0c;好了废话不多说了&#xff0c;接下来让我们看看吧 2. 开始 在开始之前需要提问下大家, 代码i ; 能保持原子性吗&#xff1f;&#xff1f;&#xff1f; 是不是一句话就执…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023