文章目录
- Day27_回溯算法
- 13. 子集 II
- 14. 491.递增子序列
- 15. 全排列
- 全排列 II
Day27_回溯算法
13. 子集 II
90. 子集 II
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
int nums_size = nums.size();
for (int i = startIndex; i < nums_size; i++) {
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
used[i] = false;
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end());
backtracking(nums, 0, used);
return result;
}
};
不适用 used 数组
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
result.push_back(path);
int nums_size = nums.size();
for (int i = startIndex; i < nums_size; i++) {
if (i > startIndex && nums[i] == nums[i - 1]) continue; // 对同一树层使用过的元素进行跳过
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end());
backtracking(nums, 0);
return result;
}
};
14. 491.递增子序列
题目:
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
思路:
找单调递增的序列,利用数组哈希去重
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
if (path.size() > 1) {
result.push_back(path);
}
int used[201] = {0}; // 这里使用数组来进行去重操作,题目说数值范围[-100, 100]
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back())
|| used[nums[i] + 100] == 1) {
continue;
}
used[nums[i] + 100] = 1; // 记录这个元素在本层用过了,本层后面不能再用了
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> findSubsequences(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
15. 全排列
46. 全排列
思路:
全排列是有序的,使用过的数字有可能再使用一次,所以不使用
startIndex
但是不能在一个排列中出现同一元素多次使用的情况,所以要使用一个used数组记录当前使用过的数字
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, vector<bool>& used) {
int nums_size = nums.size();
if (path.size() == nums_size) {
result.push_back(path);
return ;
}
for (int i = 0; i < nums_size; i++) {
if (used[i] == true) continue;
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
public:
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
全排列 II
47. 全排列 II
思路:
集合中出现重复元素,则会有重复的排列结果,需要对结果去重
- 排序
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, vector<bool>& used) {
int nums_size = nums.size();
if (path.size() == nums_size) {
result.push_back(path);
return ;
}
for (int i = 0; i < nums_size; i++) {
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue; // 去重
if (used[i] == false) { // 只能使用当前序列中没用过的元素
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, used);
used[i] = false;
path.pop_back();
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end()); // 前期要排序,后期去重要用到
backtracking(nums, used);
return result;
}
};
一个很有意思的点
去重时用
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
或者
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) continue;
都能得到正确的结果,区别是:
对于排列问题,树层上去重(前者)和树枝上去重(后者),都是可以的,但是树层上去重效率更高!
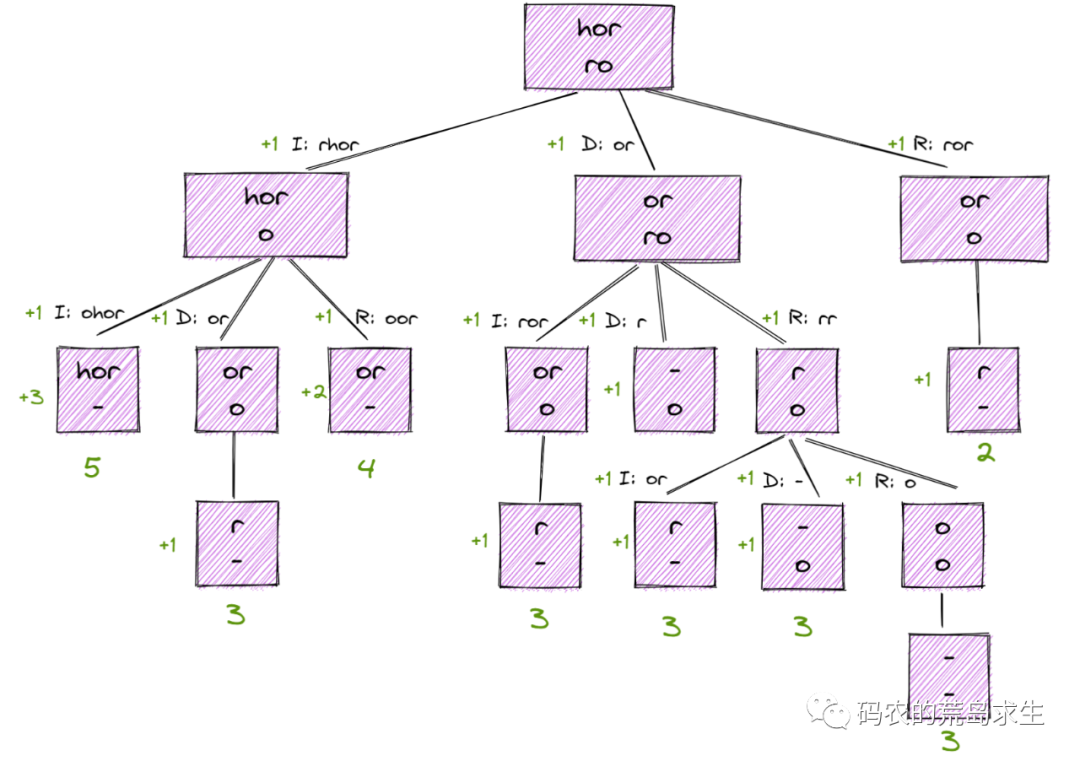
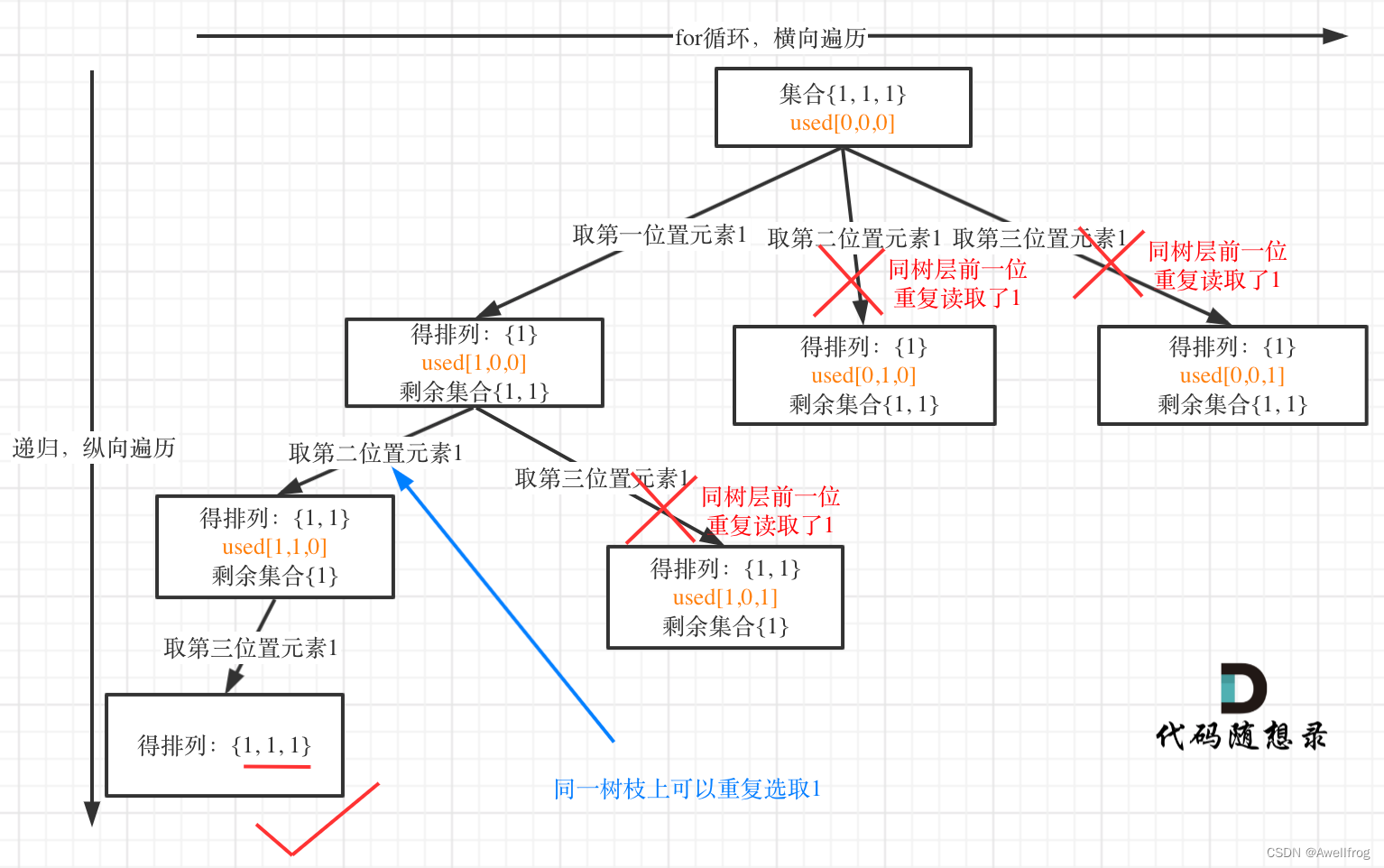
以 [1,1,1] 为例:
- 树层上去重(used[i - 1] == false),的树形结构如下:
- 树枝上去重(used[i - 1] == true)的树型结构如下:
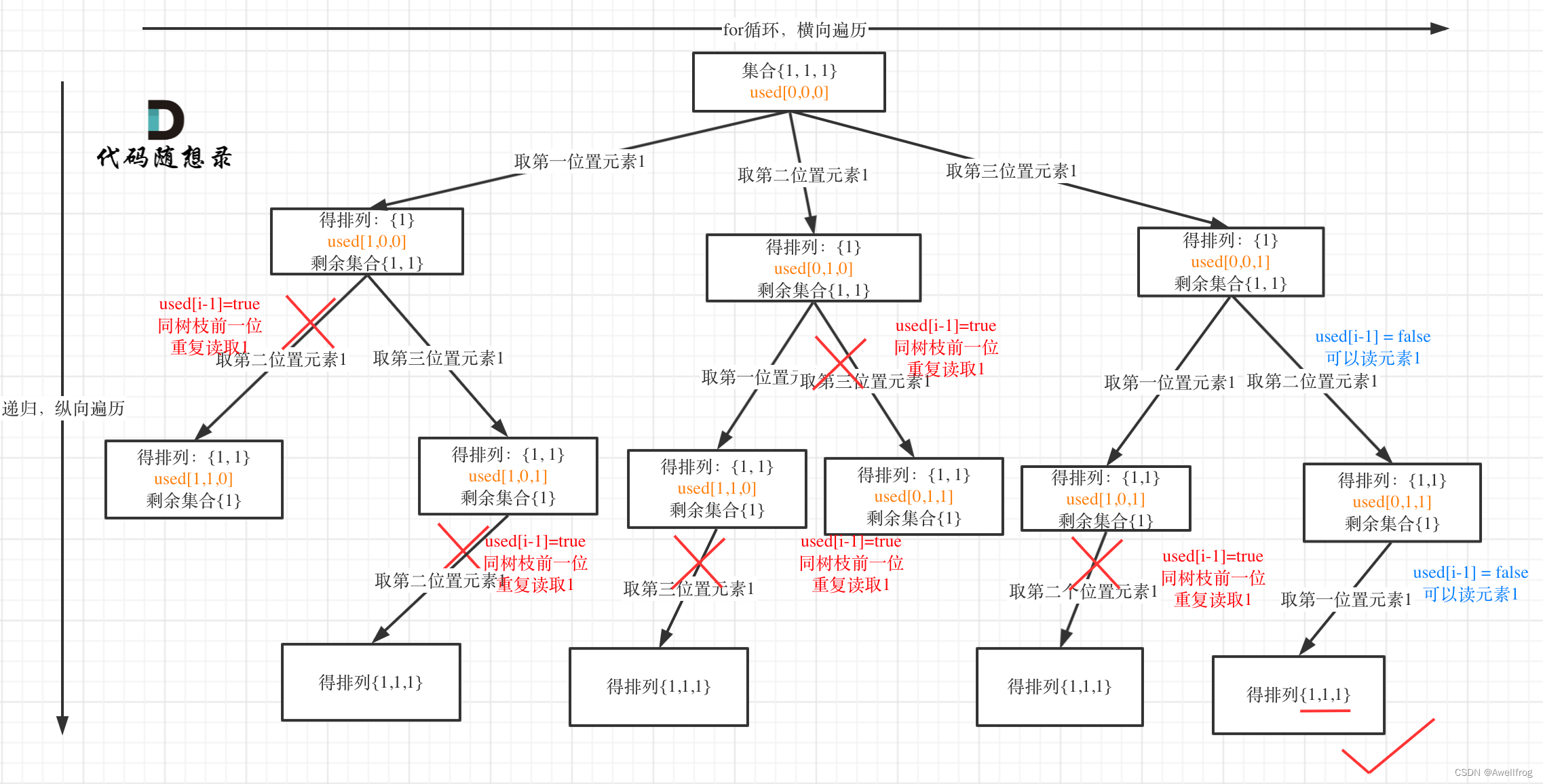
很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
![[SwiftUI 开发] Widget 小组件](https://img-blog.csdnimg.cn/aaaf16390713467186f8f6e7490ff282.png)