本篇的题目非常经典,几乎是面试必备,即,编辑距离问题,edit distance;
给定两个字符串word1以及word2,返回将word1转为word2需要的最少步骤,在每一步中你可以针对字符串word1进行以下操作:
-
新增一个字符
-
删除一个字符
-
替换一个字符
假如word1是"horse",word2是“ros”,那么你的程序需要返回3,也就是说将word1转为word2至少需要三个步骤:
-
将word1中的第一个字符h替换为字符r:horse -> rorse,此时word1变为rorse,word1与word2前两个字符相等
-
将word1中的第三个字符r删掉:rorse -> rose,此时word1变为rose,word1与word2的前三个字符相等
-
将word1中的最后一个字符删掉:rose -> ros,此时word1与word2相等。
想一想该怎样用动态规划解决这个问题。
选择与子问题
和之前的题目一样,你首先应该找出子问题是什么,子问题与原始问题的依赖关系是什么。
找出子问题的关键在于每一步的选择。
如果word1与word2的第一个字符相等,假设word1是hor、word2是hr,那么我们可以放心的排除掉两个字符串的第一个字符,即EditDistance("hor", "hr")一定等于EditDistance("or", "r"):

此时我们得到了一个子问题EditDistance("or", "r"),原始问题EditDistance("hor", "hr")的值等于该子问题。
真正有趣的是如果word1与word2的第一个字符不相等的情况,假设word1为“hor”,而word2为“ro”,此时根据该问题的规则针对word1的第一个字符有三种操作:
1,在word1的第一个字符前新增(Insert)一个字符r,此时word1变为rhor,由于此时word1 的第一个字符等于word2的第一个字符,可以放心的忽略掉,因此我们得到了子问题EditDistance("hor","o"),由于执行了一次新增操作,因此:
EditDistance("hor","ro") = EditDistance("hor","o") + 1
2,将word1的第一个字符删掉(Delete),此时word1变为“or”,我们得到了一个新的子问题EditDistance("or","ro"),由于执行了一次删除操作,因此:
EditDistance("hor","ro") = EditDistance("or","ro") + 1
3,将word1的第一个字符替换(Replace )为r,此时word1变为了“ror”,由于word1的第一个字符等于word2的第一个字符,因此可以放心的忽略掉,我们得到了一个新的子问题EditDistance("or","o"),由于执行了一次删除操作,因此:
EditDistance("hor","ro") = EditDistance("or","o") + 1
根据题目要求,我们需要得到最小的编辑距离,因此:
EditDistance("hor","ro") = min(EditDistance("hor","o"),
EditDistance("or","ro"),
EditDistance("or","o")) + 1
即:

可以看到,如果word1与word2的第一个字符如果不相等的话那么我们会得到三个子问题,取这三个子问题的最小值然后加1就是原始问题的解。
现在我们找到了子问题与原始问题之间的依赖关系。
实际上,根据上述讨论我们还可以进一步扩展从而得到完整的状态空间树。
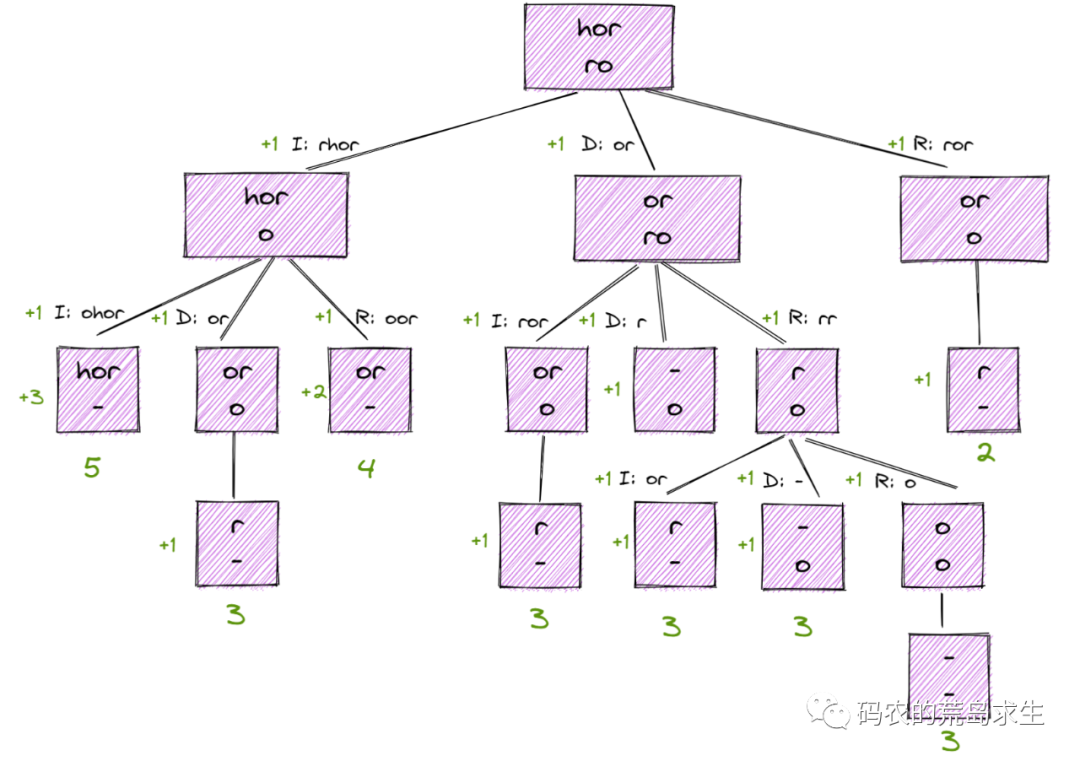
从这棵树中可以看到最小的编辑距离是2。
现在你应该清楚的知道该怎样我们是怎样一步步将问题不断的分解为更小的子问题,然后利用子问题的解来得到原始问题的解了。
自顶向下递归代码
上图中每个方框都是一个子问题,决定一个子问题的因素在于word1与word2当前处理到了哪个位置,假设对word1处理到了第i个位置,对word2处理到了第j个位置,因此我们可以对问题进行定义:
int EditDistance(int i, int j);
该函数表示从i到word1的末尾形成的字符串与从j从word2的末尾形成的字符串的编辑距离。
因此如果调用该函数时我们应该这样使用:
EditDistance(0, 0);
有了该定义与上述分析,你可以轻而易举的写出这样的递归代码:
string word1;
string word2;
int EditDistance(int i, int j) {
if (i == word1.length() && j == word2.length()) return 0;
if (i == word1.length()) return word2.length() - j;
if (j == word2.length()) return word1.length() - i;
if (word1[i] == word2[j]) return EditDistance(i + 1, j + 1);
else {
return min(EditDistance(i + 1, j + 1), min(
EditDistance(i, j + 1),
EditDistance(i + 1, j))) + 1;
}
}
我们将word1与word2声明为全局变量,这样你可以清楚的看到决定EditDistance函数值的因素只有这两个参数i和j,i的取值为[0, word1.length()],j的取值为[0, word2.length()],也就是说子问题的个数只有(word1.length() + 1) * (word2.length() + 1) 个,上述递归代码存在大量重复计算问题,因此可以通过增加cache进行优化,这个改动就留给大家啦。
接下来我们着手将自顶向下的递归代码改为自底向上的动态规划代码。
自底向上动态规划代码
由于子问题的个数只有(word1.length() + 1) * (word2.length() + 1) 个,因此可以定义一个相同大小的二维数组dp:
vector<vector<int>>dp(word1.length() + 1, vector<int>(word2.length() + 1, 0));
接下来我们要求解最小子问题,最小子问题就是上述递归代码的递归出口:
if (i == word1.length() && j == word2.length()) return 0;
该最小子问题的解包含在了dp数组的初始化中。
接下来的子问题是另外两个递归出口:
if (i == word1.length()) return word2.length() - j;
if (j == word2.length()) return word1.length() - i;
我们可以简单的构造出两种情况下的所有i和j来初始化数组dp,即:
for (int j = word2.length() - 1; j >= 0; j--)
dp[word1.length()][j] = word2.length() - j;
for (int i = word1.length() - 1; i >= 0; i--)
dp[i][word2.length()] = word1.length() - i;
最后我们利用两个for循环来构造出所有的i和j,从而将递归函数的最后一部分:
if (word1[i] == word2[j]) return EditDistance(i + 1, j + 1);
else {
return min(EditDistance(i + 1, j + 1), min(
EditDistance(i, j + 1),
EditDistance(i + 1, j))) + 1;
}
放置在for循环中,并将对递归函数的调用替换为对数组dp的读写:
for (int i = word1.length() - 1; i >= 0; i--) {
for (int j = word2.length() - 1; j >= 0; j--) {
if (word1[i] == word2[j])
dp[i][j] = dp[i + 1][j + 1];
else
dp[i][j] = min(dp[i + 1][j + 1], min(dp[i][j + 1], dp[i + 1][j])) + 1;
}
}
最终,完整的动态规划代码为:
int minDistance(string word1, string word2) {
vector<vector<int>>dp(word1.length() + 1, vector<int>(word2.length() + 1, 0));
for (int j = word2.length() - 1; j >= 0; j--)
dp[word1.length()][j] = word2.length() - j;
for (int i = word1.length() - 1; i >= 0; i--)
dp[i][word2.length()] = word1.length() - i;
for (int i = word1.length() - 1; i >= 0; i--) {
for (int j = word2.length() - 1; j >= 0; j--) {
if (word1[i] == word2[j])
dp[i][j] = dp[i + 1][j + 1];
else
dp[i][j] = min(dp[i + 1][j + 1], min(dp[i][j + 1], dp[i + 1][j])) + 1;
}
}
return dp[0][0];
}