用javascript分类刷leetcode13.单调栈(图文视频讲解)

84. 柱状图中最大的矩形 (hard)

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

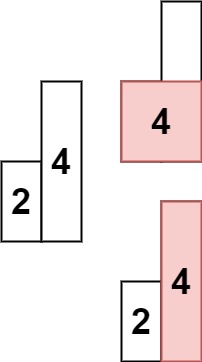
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10
示例 2：

输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

思路：准备单调递增栈存放数组下标，因为这样可以从栈顶找到左边第一个比自己小的下标，这样从当前下标出发到第一个比自己小的柱子的下标就是矩形面积的宽度，然后在乘当前柱子的高度就是面积，如果当前柱子大于栈顶的下标对应的柱子高度，就入栈，否则不断出栈，计算栈顶的柱子所能形成的矩形面积，然后更新最大矩形面积
复杂度：时间复杂度O(n)，n是heights的长度，数组里每个元素尽出栈一次。空间复杂度O(n)，栈空间最多为n

动画过大，点击查看

js：

const largestRectangleArea = (heights) => {
    let maxArea = 0
    const stack = [] //单调递增栈 注意栈存的时下标
    heights = [0, ...heights, 0]    //在heights数组前后增加两个哨兵 用来清零单调递增栈里的元素   
    for (let i = 0; i < heights.length; i++) {
        //当前元素对应的高度小于栈顶元素对应的高度时
        while (heights[i] < heights[stack[stack.length - 1]]) {
            const stackTopIndex = stack.pop() //出栈
            maxArea = Math.max(               //计算面积 并更新最大面积
                maxArea,
                heights[stackTopIndex] * (i - stack[stack.length - 1] - 1)//高乘宽
            )
        }
        stack.push(i)//当前下标加入栈
    }
    return maxArea
}

85. 最大矩形 (hard)

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

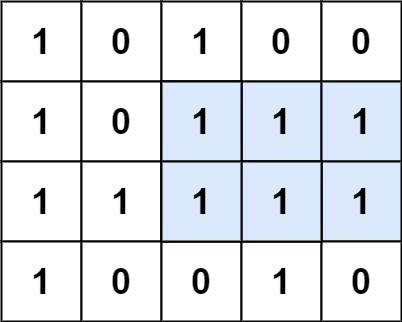
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：6
解释：最大矩形如上图所示。
示例 2：

输入：matrix = []
输出：0
示例 3：

输入：matrix = [[“0”]]
输出：0
示例 4：

输入：matrix = [[“1”]]
输出：1
示例 5：

输入：matrix = [[“0”,“0”]]
输出：0

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 ‘0’ 或 ‘1’

方法1.单调栈

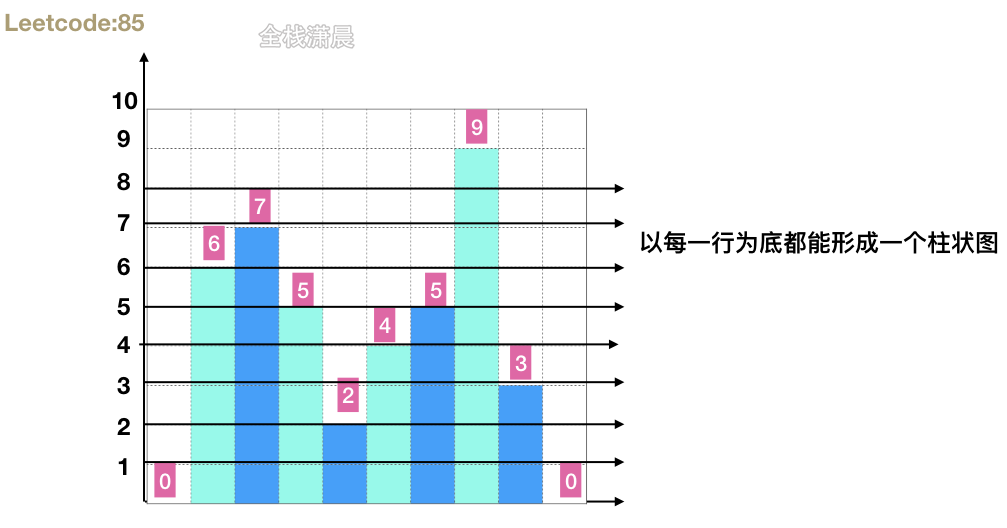
ds_106

思路：84题的变种，从第一行到第n行形成的柱状图可以利用84题求解，然后循环每一行，计算以这一行为底的柱状图最大面积，然后更新最大矩形面积
复杂度：时间复杂度O(mn)，m、n分别是矩形的高度和宽度，循环m次行，每行里循环每个柱子的高度。空间复杂度O(n)，heights数组的空间。

js：

var maximalRectangle = function (matrix) {
    if (matrix.length == 0) return 0;

    let res = 0;
    let heights = new Array(matrix[0].length).fill(0);//初始化heights数组
    for (let row = 0; row < matrix.length; row++) {
        for (let col = 0; col < matrix[0].length; col++) {
            if(matrix[row][col] == '1' ) heights[col] += 1;
            else heights[col] = 0;
        }//求出每一层的 heights[] 然后传给84题的函数
        res = Math.max(res, largestRectangleArea(heights));//更新一下最大矩形面积
    }
    return res;
};

const largestRectangleArea = (heights) => {
  let maxArea = 0
  const stack = [] //单调递增栈 注意栈存的时下标
  heights = [0, ...heights, 0]    //在heights数组前后增加两个哨兵 用来清零单调递增栈里的元素   
  for (let i = 0; i < heights.length; i++) { 
    //当前元素对应的高度小于栈顶元素对应的高度时
    while (heights[i] < heights[stack[stack.length - 1]]) { 
      const stackTopIndex = stack.pop() //出栈
      maxArea = Math.max(               //计算面积 并更新最大面积
        maxArea,                        
        heights[stackTopIndex] * (i - stack[stack.length - 1] - 1)//高乘宽
      )
    }
    stack.push(i)//当前下标加入栈
  }
  return maxArea
}

42. 接雨水（hard）

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

思路：首先考虑暴力做法，找找思路，暴力做法可以遍历数组，在每个位置分别往两边寻找左柱子中的最大高度和右柱子中的最大高度，找到之后，用左右最大高度的较小者减去当前柱子的高度，就是当前位置能接的水量。该方法要循环整个数组，并且每个位置要遍历数组寻找左右柱子高度的最大值，嵌套了一层循环，所以复杂度是O(n^2)。

我们怎样加速嵌套的这层循环呢，其实可以预先计算从左往右和从右往左的最大高度数组，在循环数组的时候，可以直接拿到该位置左右两边的最大高度，当前位置的接水量就是左右两边高度的较小者减去当前位置柱子的高度
复杂度：时间复杂度O(n)，寻找左右的最大高度，循环计算每个位置的接水量，总共3个循环，但他们不是嵌套关系。空间复杂度是O(n)，n是heights数组，用到了leftMax和rightMax数组，即存放左右两边最大高度的数组。

方法1.动态规划

动画过大，点击查看

js：

var trap = function(height) {
    const n = height.length;
    if (n == 0) {//极端情况
        return 0;
    }

    const leftMax = new Array(n).fill(0);//初始化从左往右看的最大值数组
    leftMax[0] = height[0];
    for (let i = 1; i < n; ++i) {
        leftMax[i] = Math.max(leftMax[i - 1], height[i]);
    }

    const rightMax = new Array(n).fill(0);//初始化从右往左看的最大值数组
    rightMax[n - 1] = height[n - 1];
    for (let i = n - 2; i >= 0; --i) {
        rightMax[i] = Math.max(rightMax[i + 1], height[i]);
    }

    let ans = 0;
      //循环数组，每个位置能接的雨水量就是这个位置左右最大值的较小者减去当前的高度
    for (let i = 0; i < n; ++i) {
        ans += Math.min(leftMax[i], rightMax[i]) - height[i];
    }
    return ans;
};

方法2:单调栈

动画过大，点击查看

思路：遍历heights数组，将其中的元素加入单调递减栈，如果当前柱子的高度大于栈顶柱子的高度，不断出栈，相当于找到左边比当前柱子矮的位置，然后每次出栈之后都要累加一下面积。
复杂度：时间复杂度O(n)，n是heights的长度，数组中的每个元素最多入栈出栈一次。空间复杂度O(n)，栈的空间，最多不会超过heights的长度

js：

var trap = function(height) {
    let ans = 0;
    const stack = [];//单调递减栈。存放的是下标哦
    const n = height.length;
    for (let i = 0; i < n; ++i) {//循环heights
          //当前柱子的高度大于栈顶柱子的 不断出栈
        while (stack.length && height[i] > height[stack[stack.length - 1]]) {
            const top = stack.pop();
            if (!stack.length) {//栈为空时 跳出循环
                break;
            }
            const left = stack[stack.length - 1];//拿到当前位置左边比当前柱子矮的位置
            const currWidth = i - left - 1;//计算宽度
            const currHeight = Math.min(height[left], height[i]) - height[top];//计算高度
            ans += currWidth * currHeight;//计算当面积
        }
        stack.push(i);//加入栈
    }
    return ans;
};

方法3.双指针

动画过大，点击查看

思路：如果右边存在一个比当前高的柱子，就会形成一个洼地，同理，左边存在一个比当前高柱子，也会形成一个坑，用双指针循环heights数组，判断是否形成洼地，如果能形成洼地，则计算积水量，累加进ans。
复杂度：时间复杂度O(n)，n为heights的长度，总共遍历heights一次。空间复杂度O(1)，只用到了两个指针

js：

var trap = function(height) {
    let ans = 0;
    let left = 0, right = height.length - 1;//初始化双指针
    let leftMax = 0, rightMax = 0;//左右两边最大高度
    while (left < right) {//循环双指针
        leftMax = Math.max(leftMax, height[left]);//左边最大值
        rightMax = Math.max(rightMax, height[right]);//右边最大值
        if (height[left] < height[right]) {//右边的柱子高于左边的柱子 计算这个位置的接水量 累加进结果
            ans += leftMax - height[left];
            ++left;
        } else {    //左边的柱子高于或等于右边的柱子 计算这个位置的接水量 累加进结果
            ans += rightMax - height[right];
            --right;
        }
    }
    return ans;
};

239. 滑动窗口最大值 (hard)

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置最大值

[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2：

输入：nums = [1], k = 1
输出：[1]

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length

方法1.优先队列

动画过大，点击查看

思路：最大值问题我们可以采用大顶堆，具体就是维护一个大顶堆，初始的时候将0～k-1的元素加入堆中，存入的是值和索引的键值队，然后滑动窗口从从索引为k的元素开始遍历，将新进入滑动窗口的元素加堆中，当堆顶元素不在滑动窗口中的时候，不断删除堆顶堆元素，直到最大值在滑动窗口里。
复杂度分析：时间复杂度O(nlogn)，n是nums的长度，将一个元素加入优先队列的时间复杂度是logn，最坏的情况下所有元素都要入队，所以复杂度是nlogn。空间复杂度是O(n)，最坏的情况下，所有元素都在队列中，所以是O(n)

js:

class Heap {
    constructor(comparator = (a, b) => a - b, data = []) {
        this.data = data;
        this.comparator = comparator;//比较器
        this.heapify();//堆化
    }

    heapify() {
        if (this.size() < 2) return;
        for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
            this.bubbleDown(i);//bubbleDown操作
        }
    }

    peek() {
        if (this.size() === 0) return null;
        return this.data[0];//查看堆顶
    }

    offer(value) {
        this.data.push(value);//加入数组
        this.bubbleUp(this.size() - 1);//调整加入的元素在小顶堆中的位置
    }

    poll() {
        if (this.size() === 0) {
            return null;
        }
        const result = this.data[0];
        const last = this.data.pop();
        if (this.size() !== 0) {
            this.data[0] = last;//交换第一个元素和最后一个元素
            this.bubbleDown(0);//bubbleDown操作
        }
        return result;
    }

    bubbleUp(index) {
        while (index > 0) {
            const parentIndex = (index - 1) >> 1;//父节点的位置
            //如果当前元素比父节点的元素小，就交换当前节点和父节点的位置
            if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
                this.swap(index, parentIndex);//交换自己和父节点的位置
                index = parentIndex;//不断向上取父节点进行比较
            } else {
                break;//如果当前元素比父节点的元素大，不需要处理
            }
        }
    }

    bubbleDown(index) {
        const lastIndex = this.size() - 1;//最后一个节点的位置
        while (true) {
            const leftIndex = index * 2 + 1;//左节点的位置
            const rightIndex = index * 2 + 2;//右节点的位置
            let findIndex = index;//bubbleDown节点的位置
            //找出左右节点中value小的节点
            if (
                leftIndex <= lastIndex &&
                this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
            ) {
                findIndex = leftIndex;
            }
            if (
                rightIndex <= lastIndex &&
                this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
            ) {
                findIndex = rightIndex;
            }
            if (index !== findIndex) {
                this.swap(index, findIndex);//交换当前元素和左右节点中value小的
                index = findIndex;
            } else {
                break;
            }
        }
    }

    swap(index1, index2) {//交换堆中两个元素的位置
        [this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
    }

    size() {
        return this.data.length;
    }
}

var maxSlidingWindow = function(nums, k) {
    let ans = [];
    let heap = new Heap((a, b) => b.val - a.val);//大顶堆
    for(let i=0;i<k-1;i++) heap.offer({val: nums[i], index: i});//初始的时候将0～k-1的元素加入堆中
    for(let i=k-1; i<nums.length; i++){//滑动窗口从从索引为k-1的元素开始遍历
        heap.offer({val: nums[i], index: i});//将新进入滑动窗口的元素加堆中
      //当堆顶元素不在滑动窗口中的时候，不断删除堆顶堆元素，直到最大值在滑动窗口里。
        while(heap.peek().index<=i-k) heap.poll();
        ans.push(heap.peek().val);//将在滑动窗口里的最大值加入ans
    }
    return ans;
}

方法2.单调队列

动画过大，点击查看

思路：维护单调递减队列，当进入滑动窗口的元素大于等于队尾的元素时不断从队尾出队，直到进入滑动窗口的元素小于队尾的元素，才可以入队，以保证单调递减的性质，当队头元素已经在滑动窗口外了，移除对头元素，当i大于等于k-1的时候，单调递减队头就是滑动窗口的最大值
复杂度分析：时间复杂度O(n)，n是nums的长度，每个元素入队一次。空间复杂度O(k)，队列最多存放k大小的元素

js:

var maxSlidingWindow = function (nums, k) {
    const q = [];//单递减的双端队列
    const ans = [];//最后的返回结果
    for (let i = 0; i < nums.length; i++) {//循环nums
        //当进入滑动窗口的元素大于等于队尾的元素时 不断从队尾出队，
        //直到进入滑动窗口的元素小于队尾的元素，以保证单调递减的性质
        while (q.length && nums[i] >= nums[q[q.length - 1]]) {
            q.pop();
        }
        q.push(i);//元素的索引入队
        while (q[0] <= i - k) {//队头元素已经在滑动窗口外了，移除对头元素
            q.shift();
        }
        //当i大于等于k-1的时候，单调递减队头就是滑动窗口的最大值
        if (i >= k - 1) ans.push(nums[q[0]]);
    }
    return ans;
};

496. 下一个更大元素 I (easy）

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置右侧的第一个比 x 大的元素。

给你两个没有重复元素的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的下一个更大元素。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的下一个更大元素。

示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：

4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
示例 2：

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：

2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

提示：

1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 104
nums1和nums2中所有整数互不相同
nums1 中的所有整数同样出现在 nums2 中

进阶：你可以设计一个时间复杂度为 O(nums1.length + nums2.length) 的解决方案吗？

动画过大，点击查看

思路：
1. 循环nums2，如果循环的元素大于栈顶元素，并且栈不为空，则不断将栈顶元素作为key，当前元素作为value加入map中
2. 本质是第一个比栈顶元素大的值会让栈中的元素不断出队所以这个数就是这些出栈元素的下一个更大的数
3. 剩下来的元素就是没有找到最大值的
4. 遍历nums1将结果推入ans中
复杂度：时间复杂度O(m+n)，nums1、nums2遍历一遍，nums2中的元素入队出队一次。空间复杂度O(n)，栈空间和map的空间的复杂度

js：

let nextGreaterElement = function(nums1, nums2) {
    let map = new Map(), stack = [], ans = [];
  //循环nums2，如果循环的元素大于栈顶元素，并且栈不为空，则不断将栈顶元素作为key，当前元素作为value加入map中
  //本质是第一个比栈顶元素大的值会让栈中的元素不断出队 所以这个数就是这些出栈元素的下一个更大的数
    nums2.forEach(item => {
        while(stack.length && item > stack[stack.length-1]){
            map.set(stack.pop(), item)
        };
        stack.push(item);
    });
    stack.forEach(item => map.set(item, -1));//剩下来的元素就是没有找到最大值的
    nums1.forEach(item => ans.push(map.get(item)));//遍历nums1将结果推入ans中
    return ans;
};