单调栈单调队列专题

文章目录

- - 一、单调栈
  - - 1、问题模型
    - 2、实现过程：
    - 3、代码实现
    - 4、规律总结
    - 5、题目练习
  - 二、单调队列
  - - 1、问题模型
    - 2、实现过程：
    - 3、代码实现
    - 4、规律总结
    - 5、题目练习
  - 三、总结

一、单调栈

1、问题模型

主要解决一类问题： $O (n)$ 求数列中每个元素左边/右边第一个大于/小于它的数。

例如，给定一个长度为 $N$ 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 $- 1$ 。

$1≤N≤10^5$
$1≤数列中元素≤10^9$

模板题

2、实现过程：

假设现在要求数列中每个数左边第一个比它小的数。

按照朴素做法，对于每个位置都往前遍历，直到找到一个比他小的数停止。
如果数列类似于 5 4 3 2 1，那么这种思路的复杂度就是 $O(n^2)$ ，复杂度很高。

有没有什么办法优化呢？

现在有一个数列 ${2, 7, 9, 5, 8, 6, 3, ...\}$ 。
前面几个数为 {2, 7, 9}：

后面来一个 5，那么对于数列中后面再来的所有数来说，要找到左边第一个比他们小的数，有 5 在就没 7, 9 什么事了：如果是比 5 大的数，那么找到 5 就停了；如果是比 5 小的数，7, 9 也没什么用。7, 9 两个数对后面再来的数没有价值。然后 5 继续往左找到 2，该数是左边第一个小于它的数，找到了，停止。
数列中对后面来的数有价值的有 ${2, 5\}$ 。
接着来了 8，往前找第一个比它小的数，第一个找的数 5 正好比它小，停止。
数列中对后面来的数有价值的有 ${2, 5, 8\}$ 。
接着来了 6，往前找第一个比它小的数，发现前面的 8 大于 6，那么数列中后面再来的数就只会参考 6，而数 8 对后面再来的数没有价值。继续往左找到 5 比 6 小，找到了，停止。
数列中对后面来的数有价值的有 ${2, 5, 6\}$ 。
接着来了 3，往前找第一个比它小的数，发现前面的 6 大于 3，那么数列中后面再来的数就只会参考 3，而数 6 对后面再来的数没有价值。继续往左找到 5 大于 3，同样 5 对后面再来的数没有价值。继续往左找到 2 比 3 小，找到了，停止。
数列中对后面来的数有价值的有 ${2, 3\}$ 。
…

总结操作规律：
当数列后面一个数 x 来了之后，会往前遍历有价值的数，将比 x 大的数都删掉，没删掉的第一个数就是左边第一个比它小的数；如果删完之后没有数了，说明没有比 x 小的数。

按照这种寻找方式，发现每个数都会找到左边第一个比它小的数，满足了问题要求。
同时发现：
来的每个数要么 O(1) 直接找到前一个数是比他小的数，要么O(n)遍历的时候把前面没有价值的数删掉，为后面再来的数省下时间。
每个数最多会被遍历删掉 1 次，那么整个数列最多会被遍历 1 次，时间复杂度 $O (n)$ 。

这种查询方式把原来 $O(n^2)$ 的时间复杂度降为了 $O (n)$ 。

再次观察操作规律和数列中有价值的数发现：

数列中有价值的数始终是单调递增的；
每次数列中来一个数之后，都是从后往前将有价值数列中的元素依次取出判断，类似栈操作。

所以完全可以把数列中有价值的元素用栈来存储，形成了一个单调递增的栈，叫做单调栈。

3、代码实现

将上述操作规律转化为代码就为：

stack<int> stk; //利用STL中的stack实现栈
for(int i=1;i<=n;i++) //从前往后遍历所有位置
{
	int x; cin >> x; //读入当前元素
	
	while(stk.size() && stk.top() >= x) stk.pop(); //把栈顶所有大于等于当前值的元素弹出，其对后面再来的数没有价值
	
	if(!stk.size()) cout << -1 << ' '; //如果栈空了，说明左边没有比x小的元素，输出-1
	else cout << stk.top() << ' '; //否则栈顶元素即为第一个比x小的元素，将其输出
	
	stk.push(x); //将当前元素入栈
}

整体代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 200010;
int T, n, m;
int a[N];

signed main(){
	cin >> n;
	
	stack<int> stk;
	for(int i=1;i<=n;i++)
	{
		int x; cin >> x;
		
		while(stk.size() && stk.top() >= x) stk.pop();
		
		if(!stk.size()) cout << -1 << ' ';
		else cout << stk.top() << ' ';
		
		stk.push(x);
	}
	return 0;
}

4、规律总结

上述操作通过 维护单调递增栈，求出了数列中每个数左边第一个比它小的数。
同理可以 维护单调递减栈，求出数列中每个数左边第一个比它大的数。

将枚举顺序转换，从后往前枚举，便能求出数列中每个数右边第一个比它小/大的数。

5、题目练习

练习1：发射站
题意：
一共 n 个发射站排成一行，每个发射站有高度 $H_i$ ，能够向左右两边发射能量值为 $V_i$ 的能量（最两端的向中间一端）。
每个发射站发出的能量只被两边最近的且比它高的发射站接收。
求出每个发射站接收到的能量值。

$1≤N≤10^6 ,$
$1≤H_i≤2×10^9,$
$1≤V_i≤10000$

思路
每个发射站发出的能量只被两边最近的且比它高的发射站接收，也就是分别求出每个位置左右两边第一个比高度大的位置，将其能量值累加。

Code

#include<iostream>
#include<queue>
#include<stack>
using namespace std;

const int N=1000010;
int n,m;
struct Node{
	int h,val,sum;
}a[N];
int que[N];

int main(){
	cin>>n;
	for(int i=1;i<=n;i++) scanf("%d%d",&a[i].h,&a[i].val);
	
	stack<int> stk;
	for(int i=1;i<=n;i++)
	{
		while(stk.size()&&a[stk.top()].h<=a[i].h) stk.pop();
		
		if(stk.size()) a[stk.top()].sum+=a[i].val;
		stk.push(i);
	}
	
	while(stk.size()) stk.pop();
	
	for(int i=n;i>=1;i--)
	{
		while(stk.size()&&a[stk.top()].h<=a[i].h) stk.pop();
		
		if(stk.size()) a[stk.top()].sum+=a[i].val;
		stk.push(i);
	}
	
	int ans=0;
	for(int i=1;i<=n;i++) ans=max(ans,a[i].sum);
	cout<<ans;
	return 0;

	/* 数组模拟栈实现，耗时更低
	int x=0;
	for(int i=1;i<=n;i++)
	{
		while(x>0&&a[que[x]].h<=a[i].h) x--;
		
		if(x) a[que[x]].sum+=a[i].val;
		que[++x]=i;
	}
	
	x=0;
	for(int i=n;i>=1;i--)
	{
		while(x>0&&a[que[x]].h<=a[i].h) x--;
		
		if(x) a[que[x]].sum+=a[i].val;
		que[++x]=i;
	}
	*/
}

练习2：直方图中最大的矩形
题意
给定 n 个矩形，每个矩形具有相等的宽度，但可以具有不同的高度。
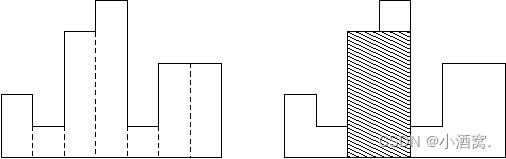
在这里插入图片描述

计算在公共基线处对齐的矩形中能够拼成的最大矩形面积。（此矩形须在公共基线处对齐）

$1≤n≤10^5,$
$0≤h_i≤10^9$

思路
这道题乍一看没有思路，这时就需要仔细观察，观察拼成的矩形特征。

发现能够拼成的矩形的高度一定是所有矩形高度中的一种。

不好直接求出形成的最大矩形，那么就直接暴力枚举所有矩形，就让当前矩形的高度作为拼成的矩形高度。
为了让该矩形的面积尽可能大，那么左右两边就要尽可能延伸，最多延伸到哪呢？
往左最多延伸到左边第一个比枚举位置高度小的位置的后一个位置，往右最多延伸到右边第一个比枚举高度小的位置的前一个位置。

用单调栈分别将两个位置求出，然后计算出以当前位置矩形的高度作为拼接矩形高度的最大矩形面积。

取所有位置的求出最大矩形面积的最大值即可。

Code

#include<bits/stdc++.h>
using namespace std;

const int N = 100010;
int n, m;
int a[N], l[N], r[N];

int main(){
	while(cin >> n && n)
	{
		for(int i=1;i<=n;i++) cin >> a[i];
		for(int i=1;i<=n;i++) l[i] = r[i] = 0;
		
		stack<int> stk;
		for(int i=1;i<=n;i++)
		{
			while(stk.size() && a[stk.top()] >= a[i]) stk.pop();
			
			if(stk.size()) l[i] = stk.top();
			stk.push(i);
		}
		while(stk.size()) stk.pop();
		for(int i=n;i>=1;i--)
		{
			while(stk.size() && a[stk.top()] >= a[i]) stk.pop();
			
			if(stk.size()) r[i] = stk.top();
			stk.push(i);
		}
		
		long long maxa = 0;
		for(int i=1;i<=n;i++)
		{
			int L = l[i], R = r[i];
			
			L ++;
			if(!R) R = n;
			else R --;
			
			maxa = max(maxa, (long long)(R - L + 1) * a[i]); //注意开longlong
		}
		cout << maxa << endl;
	}
	return 0;
}

课后练习1：仰视奶牛
课后练习2：找山坡（+思维）
课后练习3：城市游戏（练习2变式，+思维、前缀和）

二、单调队列

1、问题模型

主要解决一类问题： $O (n)$ 求数列的一个移动区间中元素的最大值/最小值。

例如，给定长度为 $n$ 的数组和定值 $k$ 。
现有一区间长度为 k，分别求出当区间右端位于 $k$ 到 $n$ 每个位置时，区间中元素的最大值和最小值。

$n≤10^6$

模板题

2、实现过程：

朴素做法，每次都遍历整个区间，最坏情况下时间复杂度为 $O(n^2)$ 。
而采用单调队列的思路可以将时间复杂度降为 $O (n)$ 。

其实，在上述单调栈的实现过程中，就可以发现：
对于求每个元素左边第一个比它小的元素，维护的单调递增栈而言，每次加入一个元素之后，当前数列中元素的最小值就存放在栈底，栈底元素就是当前数列中元素的最小值。
（对于这种现象也不难解释，每次加入一个元素的时候，这个元素都会依次把比其小的栈顶元素弹出，当数列最小值加入的时候，会把栈中所有元素弹出，那么最小值就压到栈底了）

如果我们在这个栈中只存储题目中所描述的长度为 k 的区间中的元素，那么我们把区间中所有数依次加到栈中，维护单调递增栈，就可以直接得到区间最小值了。

在区间向右移动一个位置的过程中，移出了区间最左边的一个位置，区间最右边加进来一个位置。
如果区间最左边移出的元素在维护的单调栈中的话，需要把该元素从栈中删去，然后根据新加的位置元素更新单调递增栈，将其加到栈中即可。栈底元素就是该区间的最小值。
区间每次往后移动一个位置，每次往栈中加入一个元素，当移动完整个数列时，数列中的每个数在栈中最多被遍历删除 1 次，那么就成功将时间复杂度降为 O(n)。

但中间的 如果区间最左边移出的元素在维护的单调栈中的话，需要把该元素从栈中删去 这个过程如何实现呢？
因为是从左往右依次把所有位置入栈来的维护单调递增栈，那么如果区间最左边的元素还在栈中的话，就一定是栈底元素，也就是之前区间的最小值。如果要把这个元素删掉，只需要从栈底取出一个元素删除。

在栈中如何能够从栈底取元素呢？
栈是没有办法从栈底取出元素的，为了实现这个操作只好把栈改为队列，把之前放到栈中的所有元素改为放到队列中，仿照维护单调递增栈的方式维护单调递增队列。

如果区间最左边的元素还在栈中的话，需要把该元素从栈中删去。

那么 如何判断区间最左边移出的元素在不在栈中呢？
只需要看栈底元素，即队列中队头元素的位置是不是区间最左边移出的位置。
但是此时队列中都是存的元素，元素可能会有重复，如何能够知道队头元素的位置呢？

我们需要在队列中存储元素的位置，而不是元素本身！
（知道位置 i 可以得到元素本身 a[i]，但是知道元素的值 x 却不能得到元素的位置。所以为了判断队头元素是不是区间最左边移出的元素，我们干脆在队列中存储元素位置）

分析到这里，整个实现过程就简洁明了了：
把区间中的元素位置依次加入到单调队列中，通过位置得到元素来维护单调递增队列。

在区间移动时：

1、首先判断单调队列队头位置是否是区间最左端移出的位置，如果是，将其弹出；
2、然后根据将新加入的位置更新单调递增队列；
3、将新加入的位置放到队列中。

3、代码实现

根据上述实现过程，转化为对应代码：

//求滑动窗口区间最小值
deque<int> que;
for(int i=1;i<=n;i++)
{
	cin >> a[i];
	if(que.size() && que.front() <= i - m) que.pop_front(); //1、首先判断单调队列队头位置是否是区间最左端移出的位置，如果是，将其弹出；
	while(que.size() && a[que.back()] >= a[i]) que.pop_back(); //2、然后根据将新加入的位置更新单调递增队列；
	
	que.push_back(i); //3、将新加入的位置放到队列中。
	if(i >= m) mina[i] = a[que.front()]; //该单调队列中，队头元素就是区间最小值所在位置
}

完整代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 1000010;
int T, n, m;
int a[N];
int maxa[N], mina[N];

signed main(){
	cin >> n >> m;
	
	deque<int> que;
	
	//求移动区间元素最小值
	for(int i=1;i<=n;i++) 
	{
		if(que.size() && que.front() <= i - m) que.pop_front();
		while(que.size() && a[que.back()] >= a[i]) que.pop_back();
		
		que.push_back(i);
		if(i >= m) mina[i] = a[que.front()];
	}
	
	for(int i=m;i<=n;i++) cout << mina[i] << " ";
	
	return 0;
}

同样可以手写队列：

#include<bits/stdc++.h>
using namespace std;

const int N = 1000010, mod = 1e9+7;
int T, n, m;
int a[N];
int maxa[N], mina[N];
int q[N];

signed main(){
	cin >> n >> m;

	//求移动区间元素最小值
	int st = 0, ed = -1;
	for(int i=1;i<=n;i++)
	{
		if(ed >= st && q[st] <= i - m) st ++;
		while(ed >= st && a[q[ed]] <= a[i]) ed --;
		
		q[++ed] = i;
		if(i >= m) maxa[i] = a[q[st]];
	}
	
	for(int i=m;i<=n;i++) cout << mina[i] << " ";
	
	return 0;
}

4、规律总结

因为实现原理和单调栈一样，所以规律也类似：

求区间最小值，维护单调递增栈；
求区间最大值，维护单调递减栈。

5、题目练习

练习1：最大子序和
题意
给定长度为 $n$ 的整数序列，从中找出一段长度不超过 $m$ 的连续子序列，使该子序列中元素和最大。
（子序列的长度至少是 1）

$1≤n,m≤3*10^5$

思路
一般涉及到连续子序列（子串）问题，都会用到前缀和。
就像之前见过的一道求最大子段和的题目。
那道题是求长度至少为 m 的最大连续子序列，而这道题是求长度不超过 m 的最大连续子序列。

把这两道题放在一起说。
实现思路相同，都是枚举所有位置，把当前位置作为所选子串的末位置，找到前面最佳的首位置。

之前那道题求长度至少为 m 的最大连续子序列：
对于当前末位置 i 来说，满足的首位置在区间 [1, i-m+1] 中。
已经维护出来每个位置的前缀和 s[]，那么为了使得以当前位置 i 结尾的子串元素和最大，就可以选择区间 [1, i-m] 中前缀和最小的一个值 s[j]，用当前位置前缀和 s[i] 减去这个值，便可以得到以 i 位置结尾的，最大的合法区间和。O(n) 边遍历边维护即可。

当前这道题求求长度不超过 m 的最大连续子序列也是一样：
对于当前末位置 i 来说，满足的首位置在区间 [i-m+1, i] 中。
为了使得以当前位置 i 结尾的子串元素和最大，就可以选择区间 [i-m, i-1] 中前缀和最小的一个值 s[j]，用当前位置前缀和 s[i] 减去这个值，便可以得到以 i 位置结尾的，最大的合法区间和。

对于位置 i 不断往后走，区间 [i-m, i-1] 也是不断往后走的，始终要查询这个区间的最小值，就可以用单调队列 O(n) 来维护。

Code

#include<bits/stdc++.h>
using namespace std;

#define int long long

const int N = 300010, mod = 1e9+7;
int T, n, m;
int a[N], s[N];

signed main(){
	cin >> n >> m;
	for(int i=1;i<=n;i++) cin >> a[i], s[i] = s[i - 1] + a[i];
	
	int ans = -1e18;
	
	deque<int> que;
	for(int i=1;i<=n;i++)
	{
		if(que.size() && que.front() <= i-m-1) que.pop_front();
		
		while(que.size() && s[que.back()] >= s[i - 1]) que.pop_back();
		que.push_back(i-1);
		
		if(que.size()) ans = max(ans, s[i] - s[que.front()]);
	}
	cout << ans;
	return 0;
}