209数组-长度最小的子数组

news2024/11/16 5:21:51

题目

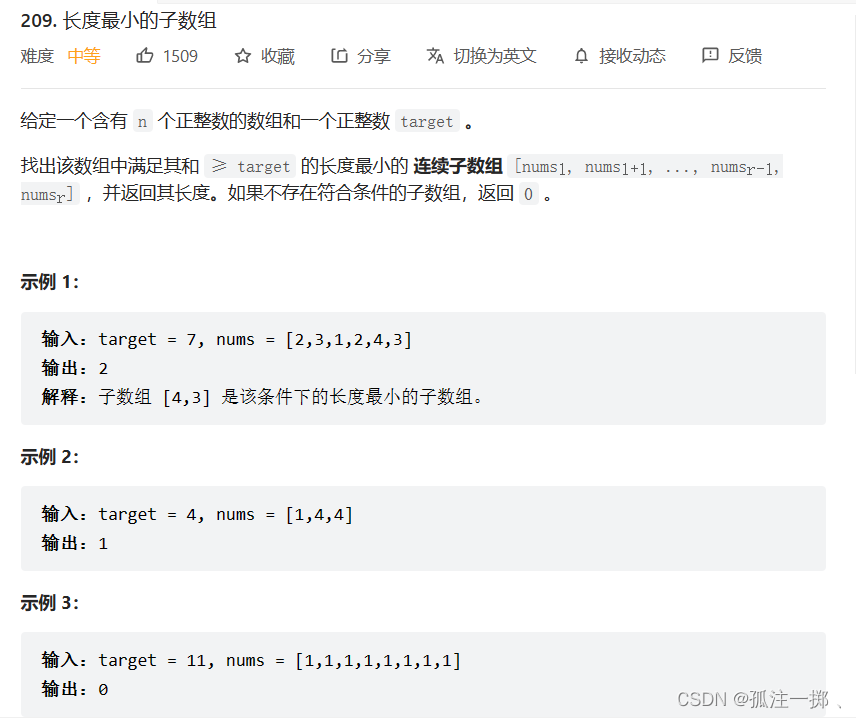
链接：209. 长度最小的子数组 - 力扣（LeetCode）

思路

可以采用暴力，两个for循环，不断寻找符合条件的子序列。时间复杂度为O(n^2)

代码：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0;
        int subLength = 0;
        for(int i = 0; i < nums.size(); i++){
            sum = 0;
            for(int j = i; j < nums.size(); j++){
                sum = sum + nums[j];
                if (sum >= target){
                    subLength = j - i + 1;
                    result = result < subLength ? result : subLength;
                    break; 
                }
            }
        }
        return result == INT32_MAX ? 0 : result;
    }
};

但是在leetcode上提交会超时。

所以采用滑动窗口的办法。

不断调节子序列的起始位置和终止位置，从而得出我们想要的结果。

用一个for循环表示滑动窗口的终止位置，如图示。

https://code-thinking.cdn.bcebos.com/gifs/209.%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.gif

窗口就是满足和大于等于target值的最小的连续子数组。

窗口的起始位置：如果当前窗口值大于target了，窗口就要向前移动。

窗口的结束位置：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

从而将O(n^2)暴力解法降为O(n)。

代码：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; //滑动窗口的数值之和
        int i = 0; //滑动窗口起始位置
        int subLength = 0; //滑动窗口的长度
        for(int j = 0; j < nums.size(); j++){
            sum = sum + nums[j];
            //这里使用while，每次更新起始位置i，并不断比较子序列是否符合条件
            while(sum >= target){
                subLength = j - i + 1; //取子序列的长度；
                result = result < subLength ? result : subLength;
                sum = sum - nums[i]; //更新起始位置i
                i++;
            }
        }
        return result == INT32_MAX ? 0 : result;
    }
};