D-一种很新的阶乘_浙江机电职业技术学院第八届新生亮相赛（同步赛） (nowcoder.com)

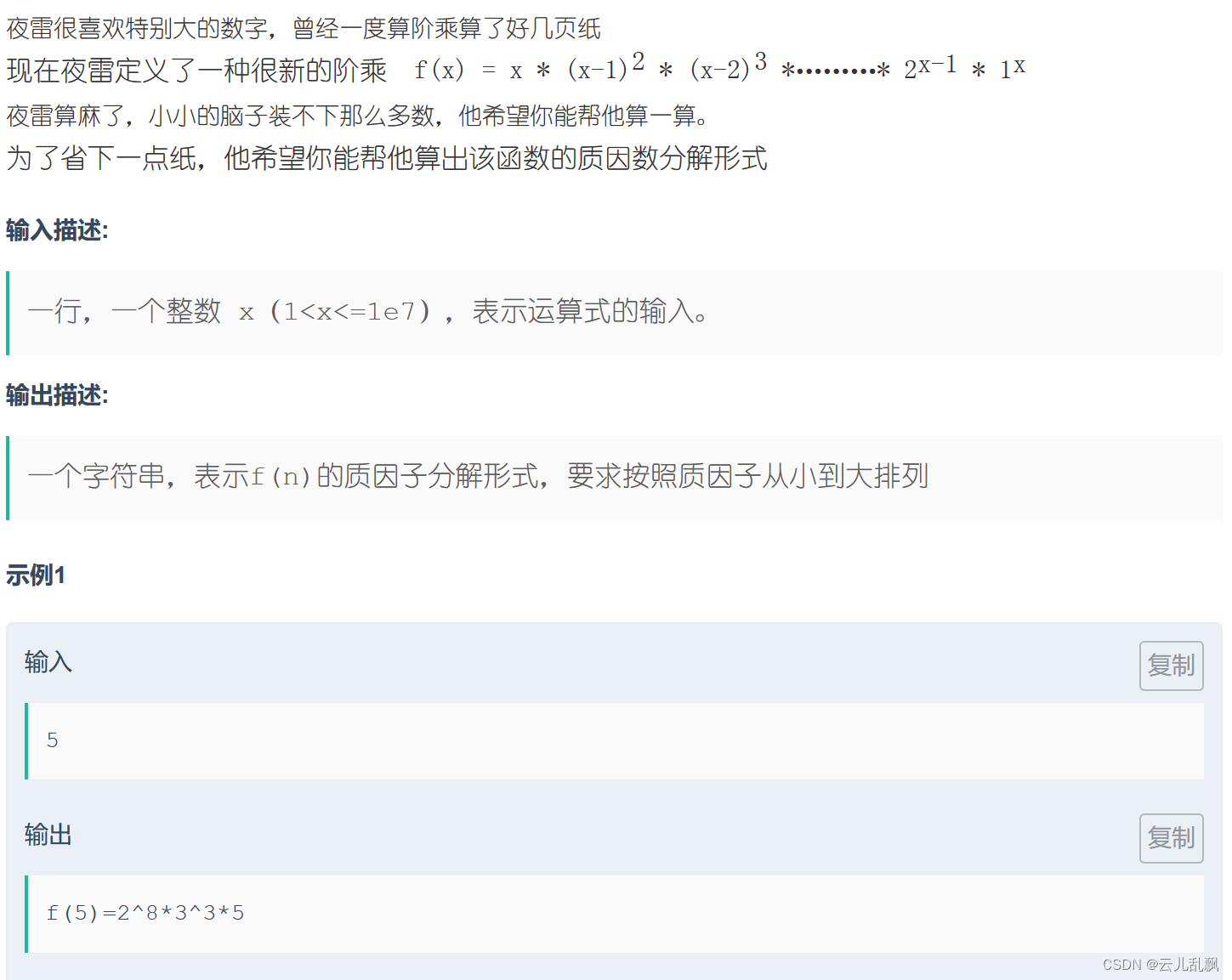        首先可以看出[1,n]中的数a的次方在初始情况下是n - a + 1，所以我们可以初始化一个w数组，w[i]存储的值为i的次方，注意w[i]的数据类型必须是long long，否则会溢出。

        题目要求我们输出f(n)的质因数分解形式，所以当a是合数时，我们要考虑将a分解，我们可以将a分解为a1 * a2，其中a1是a的最小质因子。也就是说我们要找到每个数的最小质因子，我们可以用线性筛法，每筛掉一个数就记录这个数的最小质因子，这里用数组记录，mi[i]存储i的最小质因子。

#include <iostream>
#include <string>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
#define ll long long
using namespace std;
typedef pair<int, int> PII;

const int N = 1e7 + 10;
ll st[N] = { 0 }, w[N] = { 0 }, m[N] = { 0 };
vector<ll> p;
int main() {
    ll x;
    cin >> x;
    for (int i = 1; i <= x; i++) {
        w[i] = x - i + 1;
    }
    for (int i = 2; i <= x; i++) {
        if (!st[i]) {
            p.push_back(i);
            m[i] = i; //质数的最小质因子是它自己
        }
        for (int j = 0; p[j] <= x / i; j++) {
            st[p[j] * i] = 1;
            m[p[j] * i] = p[j];
            if (i % p[j] == 0) break;
        }
    }
    for (int i = x; i >= 2; i--) {

        //i是质数，不能被分解，直接跳过
        if (m[i] == i) continue;

        //i被分解为了mi[i]和i / mi[i]，则mi[i]和i / mi[i]对应的次方都应该加上i的次方
        //i被分解后，次方应该置为0
        w[m[i]] += w[i];
        w[i / m[i]] += w[i];
        w[i] = 0;
    }
    int f = 0;
    cout << "f(" << x << ")=";
    for (ll i = 2; i <= x; i++) {
        if (w[i] == 0) continue;
        if (f) cout << "*";
        if (w[i] == 1) cout << i;
        else cout << i << "^" << w[i];
        f = 1;
    }
    return 0;
}