1802. 有界数组中指定下标处的最大值

题目描述

给你三个正整数 n、index 和 maxSum 。你需要构造一个同时满足下述所有条件的数组 nums（下标 从 0 开始 计数）：

• nums.length == n
• nums[i] 是 正整数 ，其中 0 <= i < n
• abs(nums[i] - nums[i+1]) <= 1 ，其中 0 <= i < n-1
• nums 中所有元素之和不超过 maxSum
• nums[index] 的值被 最大化

返回你所构造的数组中的 nums[index] 。

注意：abs(x) 等于 x 的前提是 x >= 0 ；否则，abs(x) 等于 -x 。

---

示例 1

输入：n = 4, index = 2, maxSum = 6
输出：2
解释：数组 [1,1,2,1] 和 [1,2,2,1] 满足所有条件。不存在其他在指定下标处具有更大值的有效数组。

---

示例 2

输入：n = 6, index = 1, maxSum = 10
输出：3

---

提示

• 1 <= n <= maxSum <= 10⁹
• 0 <= index < n

算法一：模拟

思路

• 从 index 开始往两边扩充：维护一个 [l,r] 范围，每次往范围内每个位置 +1 ，通过这种方式维护一个向上生长的“三角形”。
  

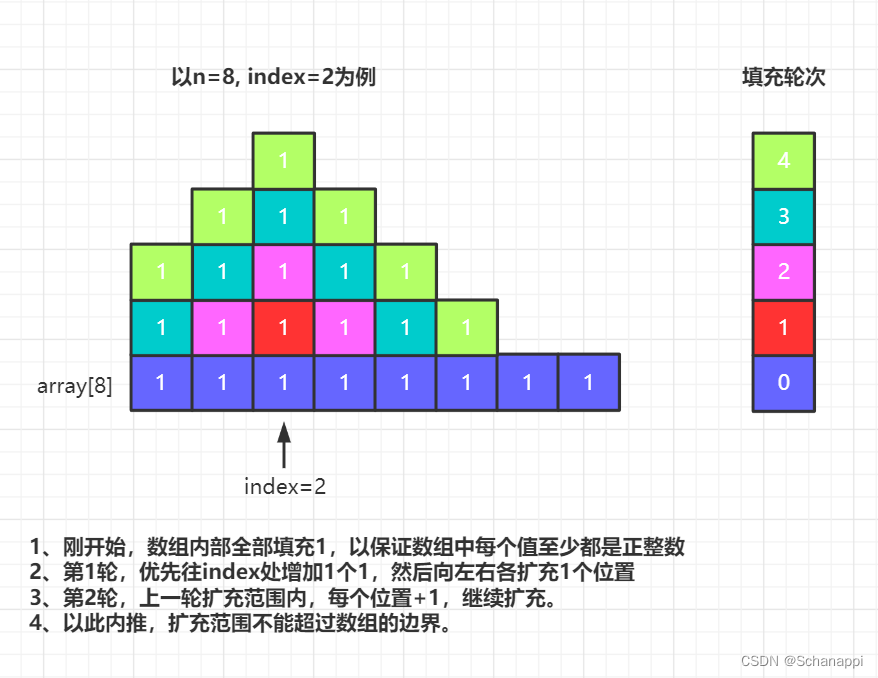
收获

• 这个图形模拟比我之前动手计算清晰很多，值得学习。

算法情况

• 时间复杂度：O（√M） ， 其中 M = n - index
• 空间复杂度：O（1）

代码

class Solution {
public:
    int maxValue(int n, int index, int maxSum) {
        int ans = 1;
        int left = index, right = index;
        // 整个数组一开始填充为1
        // rest记录全部填充为1，剩余1的个数
        int rest = maxSum - n;
        while(left > 0 || right < n-1){
            int len = right - left + 1;
            if(rest >= len){
                // 当前[l, r]范围全部+1
                rest -= len;
                ans ++;
                // 范围往两边扩大
                left = max(0, left - 1);
                right = min(right + 1, n - 1);
            }
            else break;
        }
        // 剩余的数平均分配
        ans += rest / n;

        return ans;
    }
};