1.简介

目标识别有两大经典结构: 第一类是以Faster RCNN为代表的二阶段识别方法，这种结构的第一阶段专注于proposal的提取，第二阶段则对提取出的proposal进行分类和精确坐标回归。
二阶段结构准确度较高，但因为第二阶段需要单独对每个proposal进行分类/回归，速度就打了折扣；目标识别的第二类结构是以YOLO和SSD为代表的单阶段结构，它们摒弃了提取proposal的过程，只用一级就完成了识别/回归，虽然速度较快但准确率远远比不上两级结构。那有没有办法在单阶段结构中也能实现较高的准确度呢？Focal Loss就是要解决这个问题。
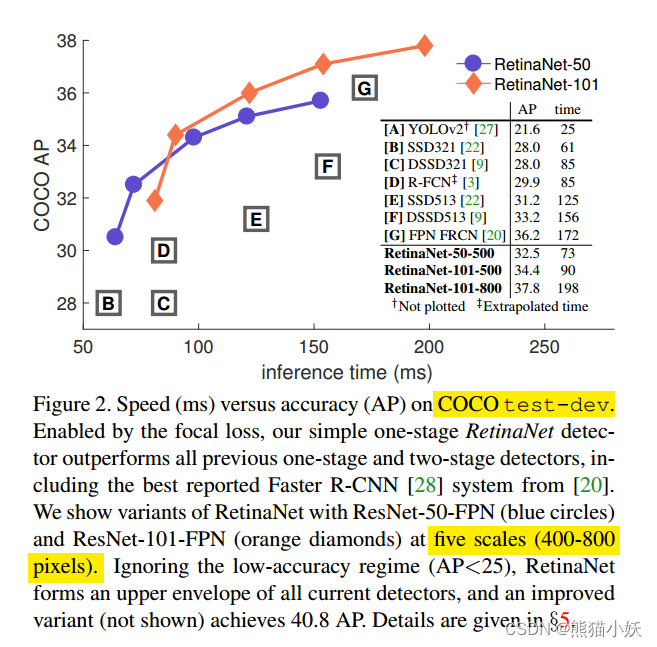
在这里插入图片描述
这是在coco数据集上的mAP指标, 可以看出要比一些单阶段的例如ssd，还有二阶段fpn faster rcnn都要高。在当时2018年的时候，还是ＳＯＴＡ的。

2.模型

2.1 二阶段要比单阶段模型效果好本质原因

作者认为，单阶段效果比二阶段差的根本原因是类别不均衡。
二阶段模型一般在训练过程，第一个阶段筛选出的proposals，这已经过滤掉了大部分的背景bbox，第二个阶段采样过程保持正负样本的一定比例，例如fixed foreground-to-background ratio (1:3), or online hard example mining (OHEM). 这样就保持了前后背景样本的比例平衡问题。
而单阶段的模型，没有proposal，针对所有的候选位置进行采样，这些bbox大约有∼100k 左右。负样本的数量远远大于正样本的数量，造成正负样本的极不均衡。采样过程可以学习二阶段模型，但是这个过程肯定是低效的，因为训练过程还是大部分被｀easily classified background主导，所以整体的效果稍差。

而正负样本的极不平衡会造成如下影响：

在计算loss时，负样本数量很多，所以在loss中负样本的比重就很大，然而负样本比较容易分类(easy negatives)，所以给loss能提供的有用信息较少。
而正样本是我们最终要得到的检测结果，比较难分类(hard positive)，所以提供的loss信息比较重要，但是由于数量少，这些关键的loss很容易被淹没掉。

2.2 模型结构

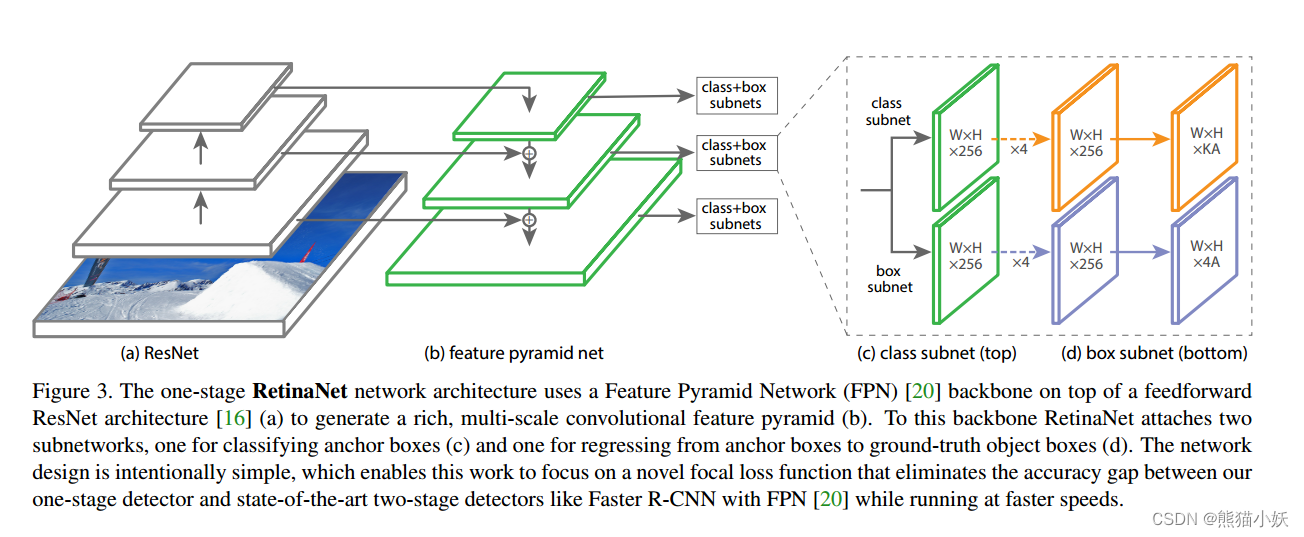
在这里插入图片描述
模型的结构中规中据
backbone: resnet 50 or 100
neck: fpn
head: dease head ( class + bbox regression)

最大的亮点是在于利用focal loss解决　关于前后背景／简单，难例不均衡问题，从而抑制easy sample,让更多的正负hard sample在loss上起到更大作用，更好的解决样本类别不均衡问题。

2.3.focal loss

2.3.1　公式说明

在这里插入图片描述

从图中可以看出，一般样本可以分为四大类：

easy negative：全是背景，比较容易判断的负样本
easy positive：全是物体，比好容易判断的正样本
hard negative：包含部分物体，但大部分为背景，比较难判断的负样本
hard positive：包含部分背景，但大部分为物体，比较难判断的正样本

可以看出hard examples就是在背景和物体过渡的区域，但是由于每张图中的物体较少，也就是正样本比较少，所有这种hard examples也比较少，同时由于负样本有很多，所以easy negative就很多，因此easy examples也就远多于hard examples。所以说正负样本不均衡可以引起hard-easy样本不均衡，进而使得loss被easy examples的loss所控制，从而使得模型没有一个有效的loss来指导训练，所以最终得到一个不好的模型，所以最后的准确率比较低。
所以我们需要Focal loss来赋予这些hard examples更多权重。
在这里插入图片描述
作者这里为了简化，拿二分类问题进行举例。

Focal loss是在交叉熵损失函数基础上进行的修改，首先回顾二分类交叉上损失：
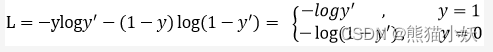
在这里插入图片描述

y’是经过激活函数的输出，所以在0-1之间。可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。那么Focal loss是怎么改进的呢？
在这里插入图片描述

首先在原有的基础上加了一个因子，其中gamma>0使得减少易分类样本的损失。使得更关注于困难的、错分的样本。
例如gamma为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的gamma次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。
此外，加入平衡因子alpha，用来平衡正负样本本身的比例不均：文中alpha取0.25，即正样本要比负样本占比小，这是因为负例易分。

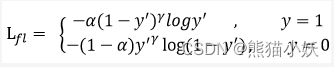
在这里插入图片描述
只添加alpha虽然可以平衡正负样本的重要性，但是无法解决简单与困难样本的问题。
gamma调节简单样本权重降低的速率，当gamma为0时即为交叉熵损失函数，当gamma增加时，调整因子的影响也在增加。实验发现gamma为2是最优。

gamma :　难例权重，越大越关注难例。gamma占主导地位。随着gamma的增大，alpha要相应的减小。
alpha：正负样本权重，越大越关注正样本。
在gamma增加的时候，alpha要适当减小。

2.3.2　其他

(1) 并不是对于所有的anchor都计算loss，只是对于存在gt的所有anchor计算loss
在这里插入图片描述

(2) 　初始化
在这里插入图片描述

在模型运行初始阶段，为了训练稳定性，设定了一个预先值π，即正样本的概率一般取到π=0.01
在这里插入图片描述
最后一层的卷积bias　b稍有不同

2.4 消融实验

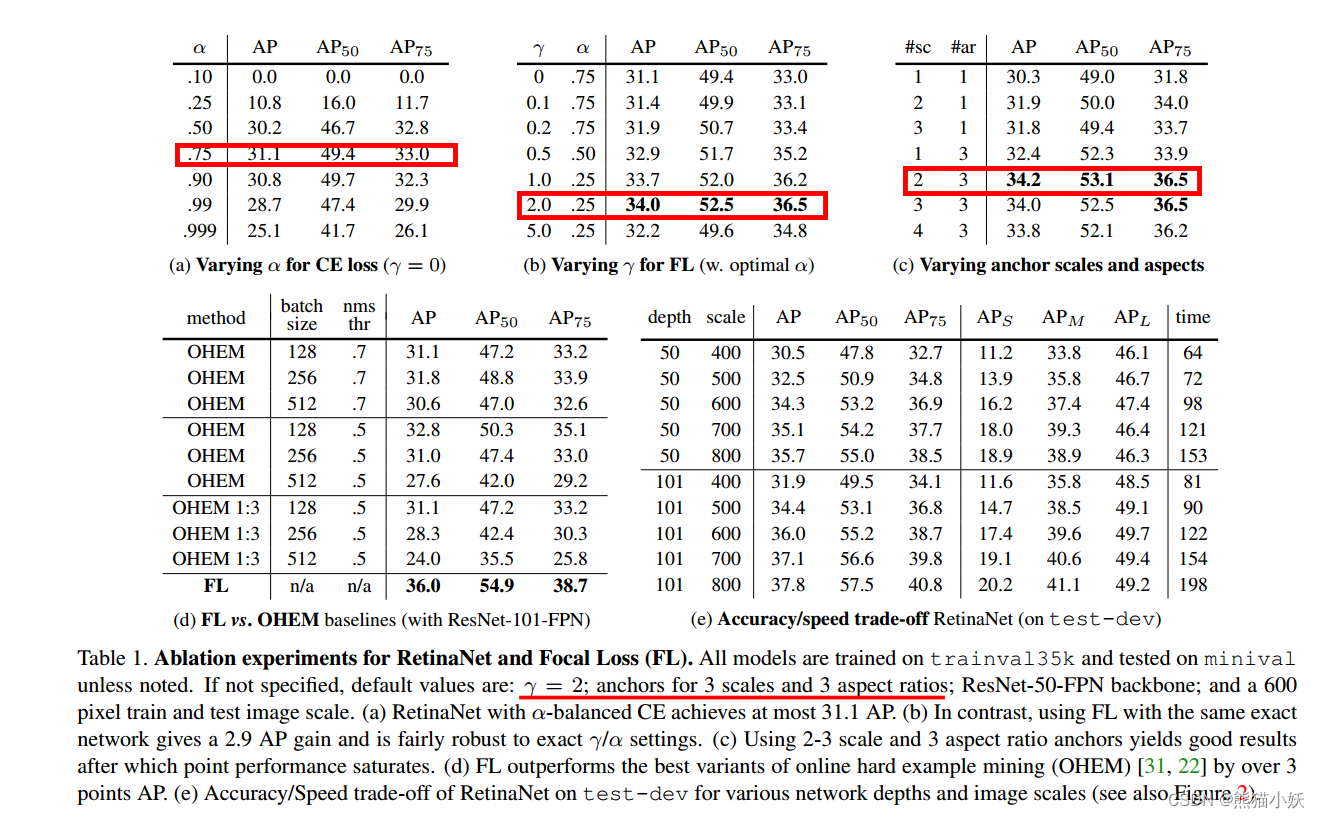
在这里插入图片描述

(a) 单独调alpha，在0.75最优
(b)　alpha+gamma : alpha降低到最小，gamma较大最好。关注negtivate hard example最好。>
© 调整anchor scale or aspect。这个也不是anchor越大越多最好
(d)　OHEM vs FL ,FL更好一些
(e)　input size尺度，　backbone大小影响

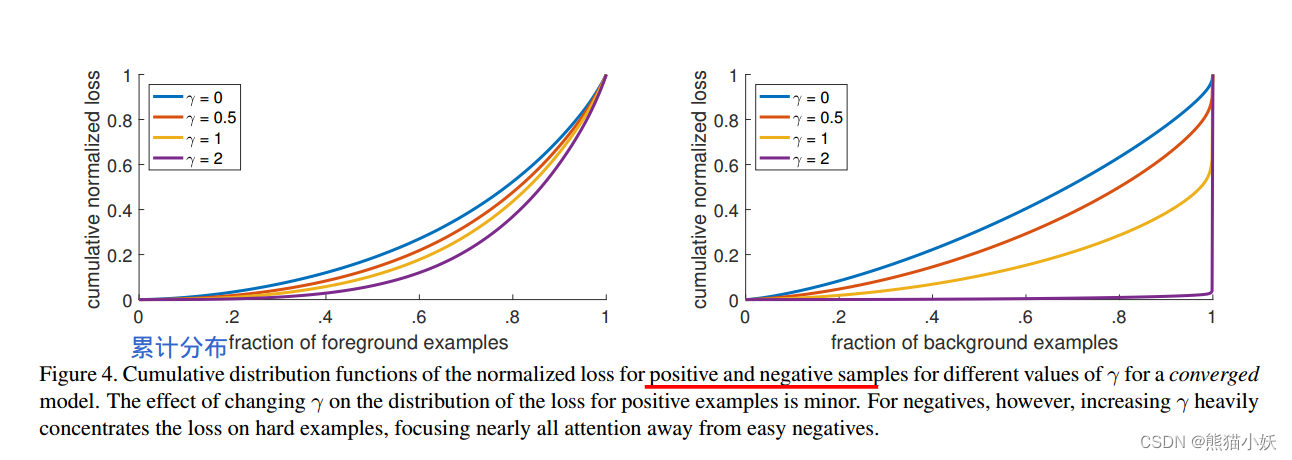
在这里插入图片描述
正样本和负样本的累积分布函数（CDF）如图4所示。如果我们观察正样本损失（左），我们会发现CDF看起来，随着gamma的增加，变化其实并不大，说明gamma对于正样本难例的提升作用较小。