b站课程链接:线性模型
1.基本思想:
给出了一组一维数据,定义了一个简单的线性拟合函数,通过穷举法来列出一些权重(拟合函数的系数),并计算这些权重对应的拟合损失函数(使用均方误差(MSE))。
Linear Model:
y
^
=
w
∗
x
\hat{y}=w*x
y^=w∗x (为了简化模型,未加偏置项b)
Training Loss (Error):
l
o
s
s
=
(
y
^
−
y
)
2
=
(
w
∗
x
−
y
)
2
loss=(\hat{y}-y)^2=(w*x-y)^2
loss=(y^−y)2=(w∗x−y)2
Mean Square Error:
c
o
s
t
=
1
N
∑
n
=
1
N
(
y
n
^
−
y
n
)
2
cost=\frac{1}{N}\displaystyle\sum_{n=1}^N(\hat{y_n}-y_n)^2
cost=N1n=1∑N(yn^−yn)2
2.课程代码:
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 定义拟合函数
def forward(x):
return x * w
# 定义损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
# 存放权重(系数)和相应损失
w_list = []
mse_list = []
# 权重使用穷举法
for w in np.arange(0.0, 4.1, 0.1):
print("w={:.2f}".format(w))
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t',"{:.2f} {:.2f} {:.2f} {:.2f}".format(x_val, y_val, y_pred_val, loss_val))
print('MSE={:.2f}'.format(l_sum / 3))
# 存储权重(系数)和相应损失
w_list.append(w)
mse_list.append(l_sum / 3)
# 可视化
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
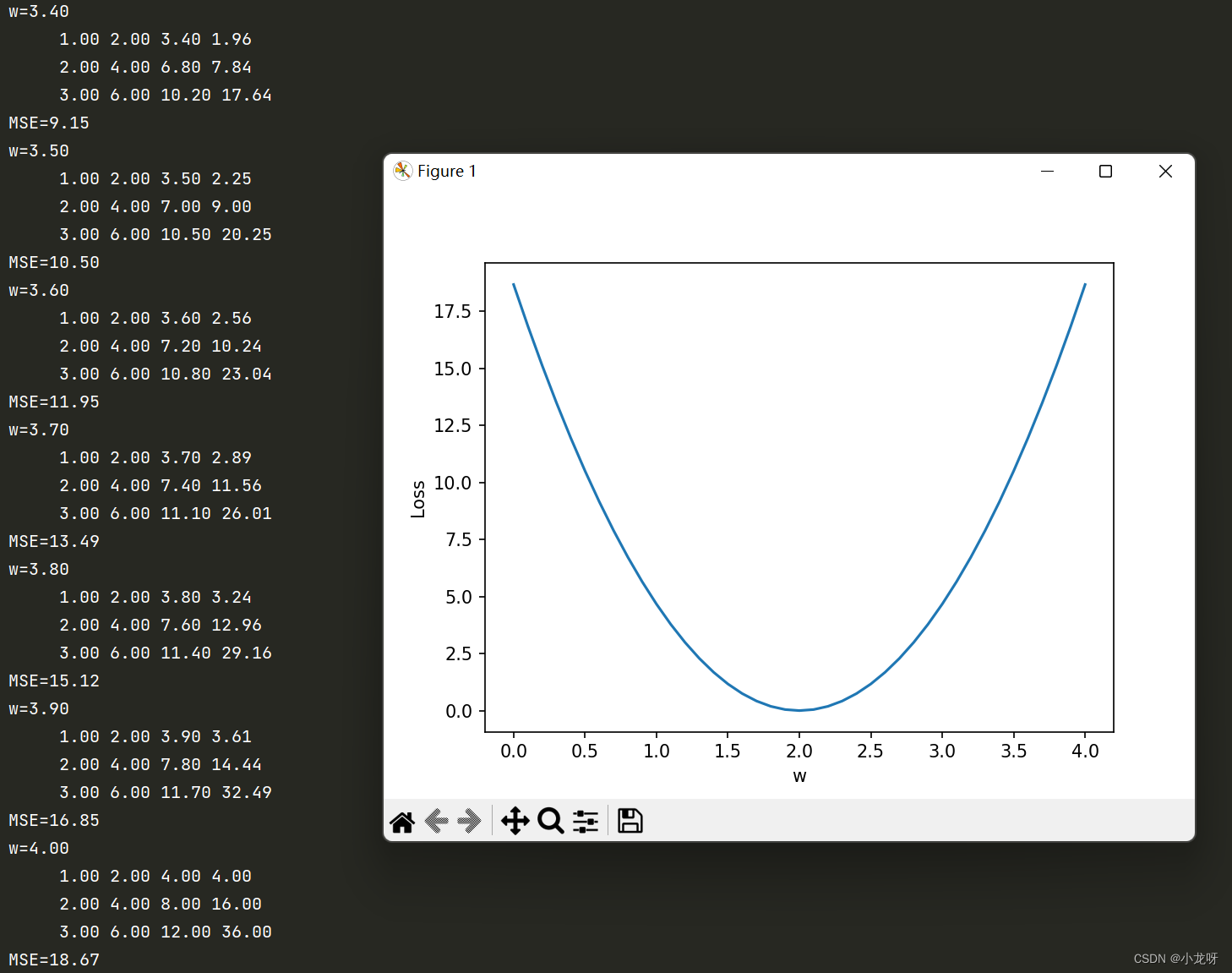
3.运行结果(部分截图):