计算机组成原理复习:数据的表示和运算
- 2. 数据的表示和运算
- 2.1 数制与编码
- 2.1.1 数制:进位计数制及其相互转换
- 2.1.2 编码:数值数据的编码与表示
- 2.1.2.1 逻辑型数据
- 2.1.2.2 字符型数据 之 ASCII码
- 2.1.2.3 数值型数据 之 BCD码
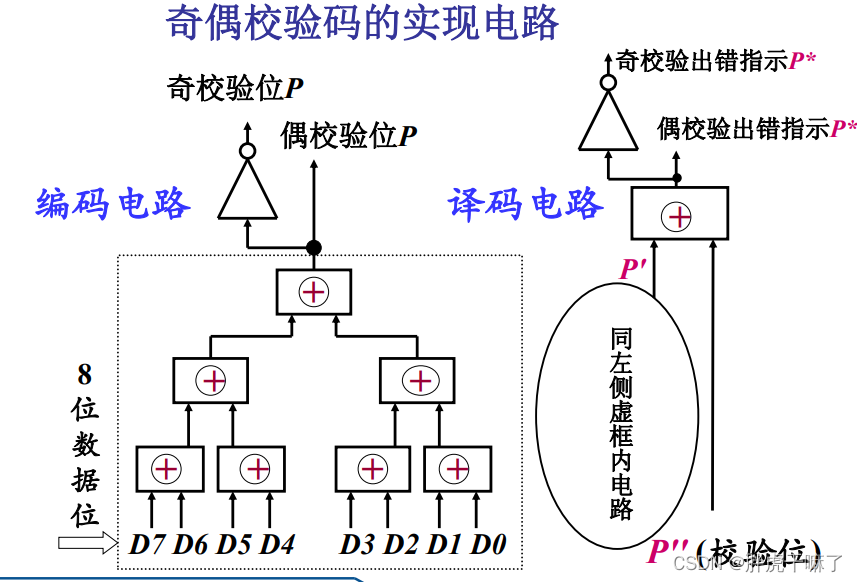
- 2.1.3 校验码——奇偶校验码
- 2.2 定点数的表示和运算
- 2.2.1 定点数的表示
- 2.2.2 定点数的运算
- 2.3 浮点数的表示和运算
- 2.3.1 浮点数的表示
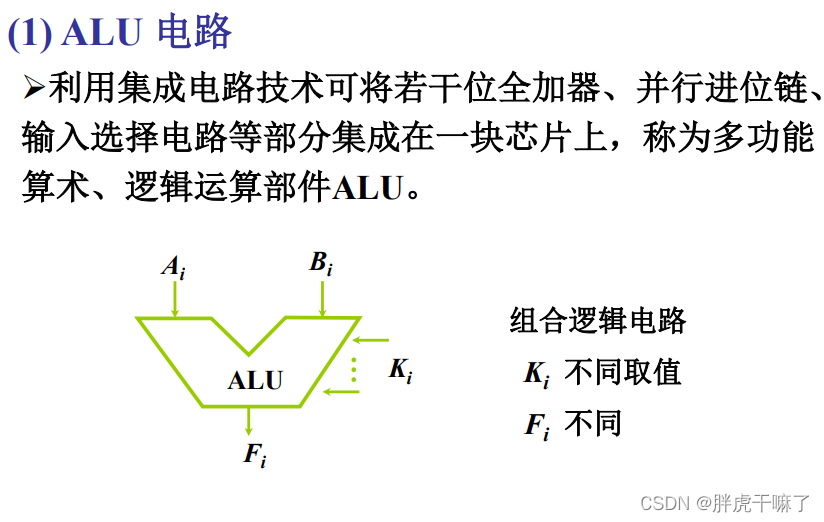
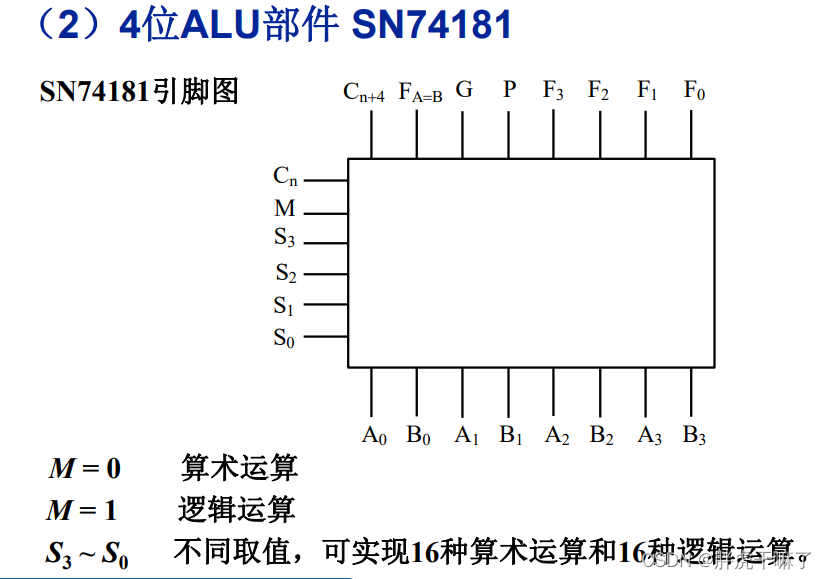
- 2.4 算术逻辑单元ALU
- 2.4.1 串行进位加法器
- 2.4.2 并行进位加法器
- 2.4.3 算术逻辑单元 ALU
2. 数据的表示和运算
主要内容:
- 数据表示、运算方法
- 二进制、十进制、十六进制之间的转换√
- 数据编码与检错纠错(奇偶校验)√
- 8421-BCD码√,ASCII码√、汉字内码
- 定点数的原码反码补码√,整数的移码√
- 定点数的加减法运算√与溢出判断√,乘法运算规则√
- 浮点数的表示√,规格化√,IEEE754标准√
- 运算器部件
- ALU组成与功能,加法器和进位方式
2.1 数制与编码
2.1.1 数制:进位计数制及其相互转换





2.1.2 编码:数值数据的编码与表示
真值:数据的数值通常以正负号后跟绝对值来表示,称之为真值
机器数:在计算机中使用的连同数符一起数码化的数值成为机器数
数据可以分为:
- 逻辑型数据
- 字符型数据:ASCII码等、字符串、汉字
- 数值型数据:定点小数、整数、浮点数、二-十进制数(BCD码)
2.1.2.1 逻辑型数据
只有两个值,1表示真,0表示假

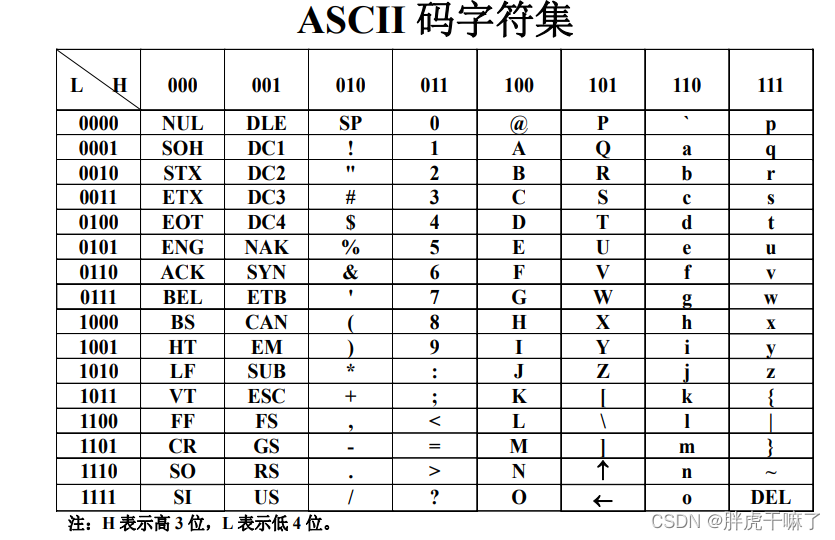
2.1.2.2 字符型数据 之 ASCII码

2.1.2.3 数值型数据 之 BCD码


2.1.3 校验码——奇偶校验码







2.2 定点数的表示和运算
2.2.1 定点数的表示
定点数:在计算机中,小数点位置固定不变的数






整数的机器数表示范围:

在小数的公式上,将所有数值乘了2n-1倍
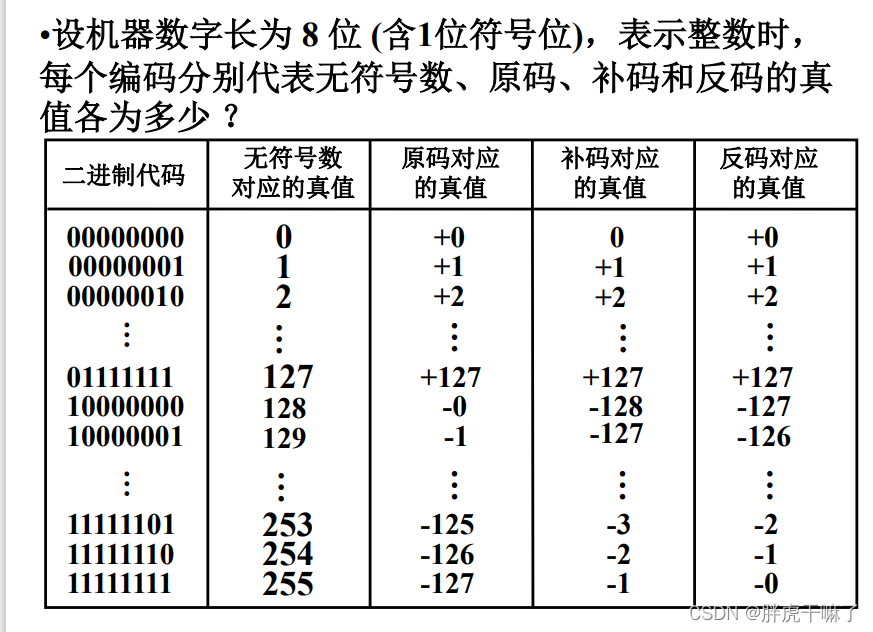
当真值小于0时,反码=补码+1


2.2.2 定点数的运算
(1)定点数的移位运算
分为算术移位和逻辑移位

(2)定点数的补码加减运算

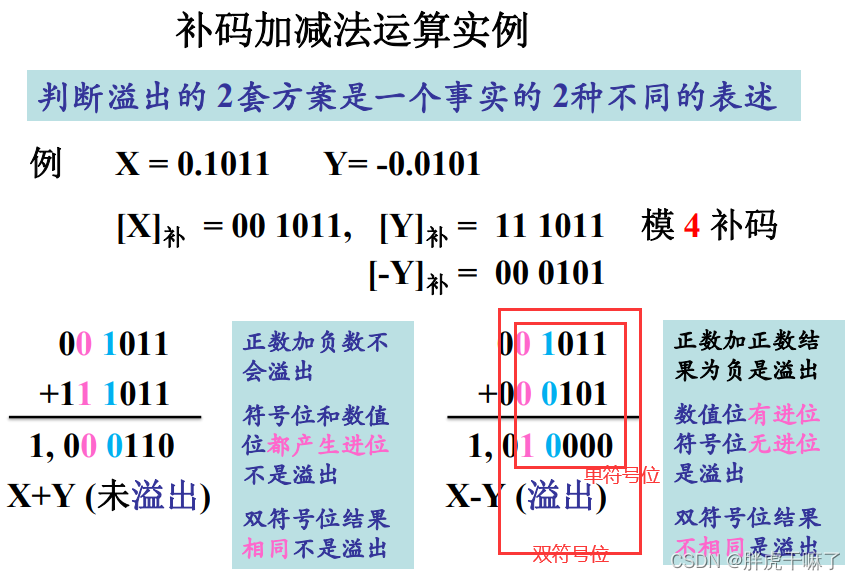
(3)溢出条件判断
溢出:当运算结果超出机器数所能表示的范围时,称为溢出
主要判别方法有:
- 单符号位:当任意符号的两个数(的补码)相加时,设Cf为最高数值位的进位,Cs为符号位的进位,如果Cf等于Cs,则运算结果正确;若不相等,则产生溢出。即溢出的判断条件为:OV=Cs异或Cf
- 双符号位:对补码进行变形,第一个符号位Sf1,第二个符号位为Sf2,(正数的双符号位为00,负数的双符号位为11)符号位直接参与运算,当结果的两个符号位不相同时,则判断为溢出,溢出的条件为OV = Sf1 异或 Sf2。当运算结果为01正溢或10负溢时,最高符号位Sf1代表其真正答案的符号。
(4)定点数的乘法运算
- 原码一位乘法:两个原码数相乘,乘积的符号位相乘的两个数的异或值,数值上为两个数的绝对值 之和
- 补码一位乘法:将乘法直接用补码进行,以减少转换次数

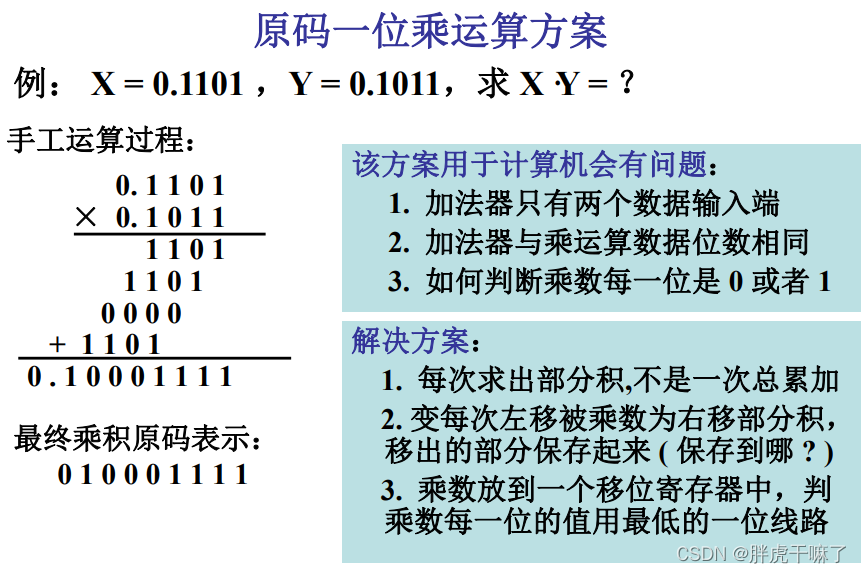
需要注意的是,在原码一位乘运算中中,我们对符号单独进行处理,再使用绝对值运算,对被乘数B和部分积A均使用双符号位,乘数末位Cn作为判断位,进行n次(累加、右移的)循环
且在最后一步加法之后,还要再进行一次移位操作



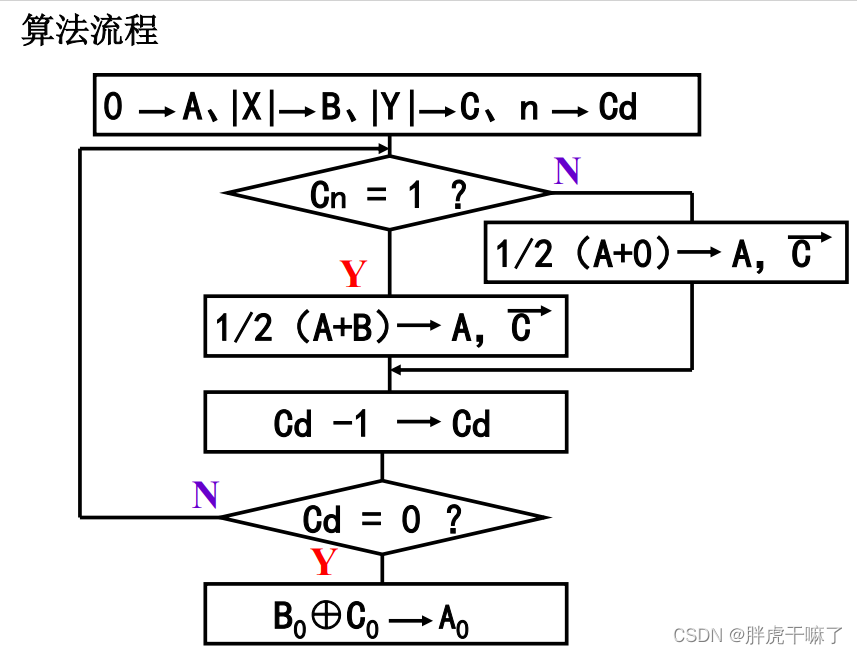
关于定点补码一位乘法:
在原码乘法中,不方便的一点是需要对符号位进行单独计算,并且在最后给乘法冠以正确的符号。
而补码乘法是采用操作数的补码进行乘法运算,最后的乘积仍然为补码,以保持乘积的正确符号




需要注意的是,相对于原码乘法,在补码乘法中,为乘数拓展出了Y0位和Yn+1位(初值均为0),以应对计算 Yn+1-Yn 的需求
另外,在移位的过程中,部分积和被乘数采取双符号位,仅参加运算而不参加移位,乘数C取单符号位,符号位参加移位,这也是与原码乘法不同的一点
最后一个与原码乘法不同的是:在第n+1步中,仅完成累加而不需要移位

2.3 浮点数的表示和运算
主要内容:浮点数的表示,规格化,IEEE754标准
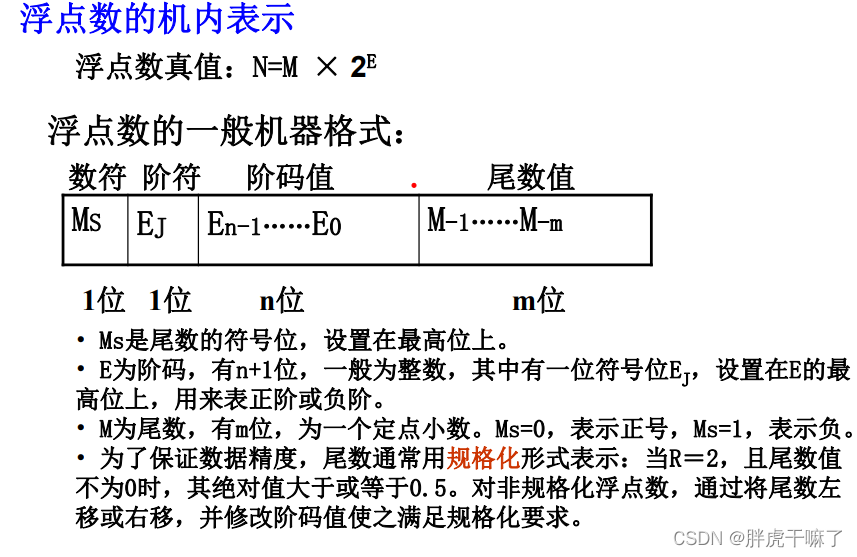
2.3.1 浮点数的表示
- 浮点数的表示范围:


- 浮点数规格化

在未进行规格化时,浮点数的表示范围:
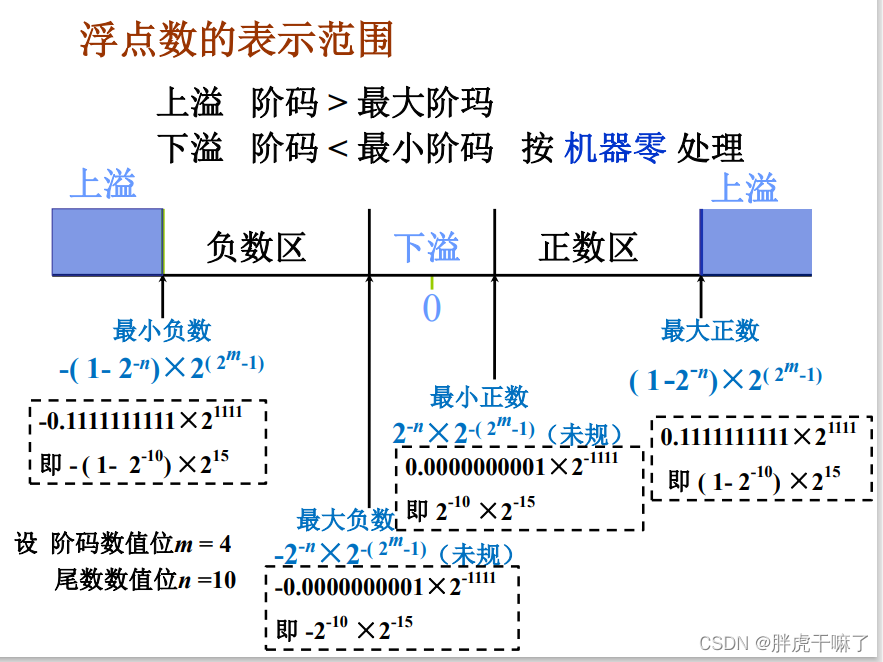
在规格化后,浮点数的绝对值的最小值要求大于等于0.5,此时浮点数表示范围:

常规的浮点数表示方法,阶码和位数部分都使用补码表示


- IEEE 754标准
需要注意的是:
IEEE754的阶码使用移码来表示,即将原码投影到非负区间内完成,是带有一定偏移量的无符号整数;
IEEE 754的尾数使用原码来表示







浮点数的加减运算,了解即可












2.4 算术逻辑单元ALU
主要内容:ALU组成与功能,加法器和进位方式
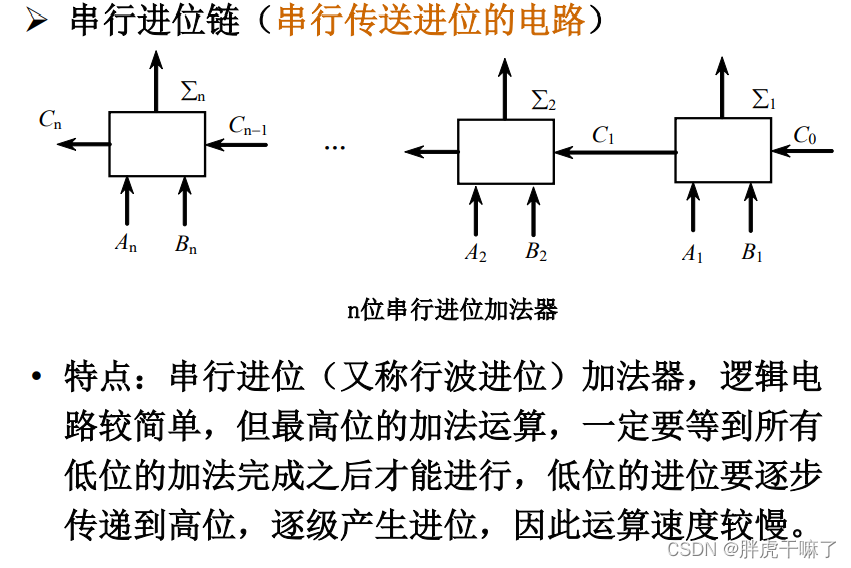
2.4.1 串行进位加法器
2.4.2 并行进位加法器
核心思想:为串行进位加法器提速——加快进位产生和传递的速度

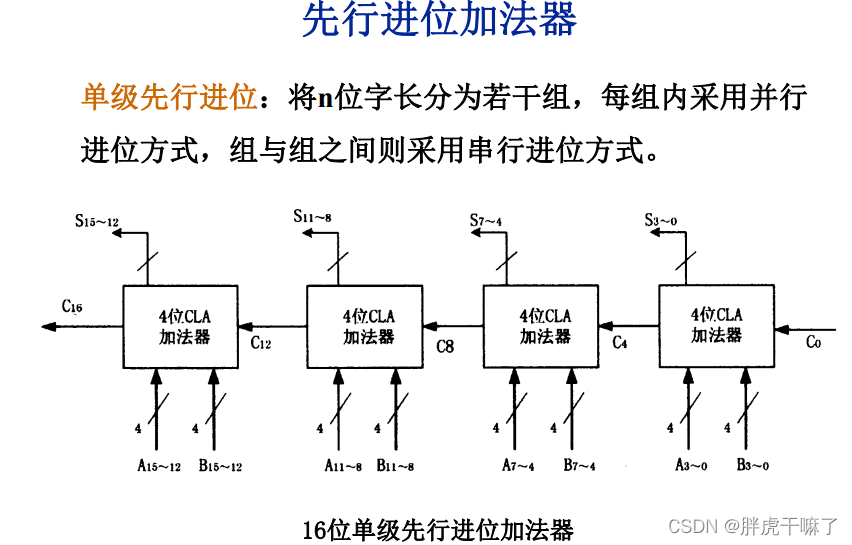
2.4.3 算术逻辑单元 ALU