图的遍历(深度DFS与广度BFS)

news2024/10/5 5:20:30

文章目录

        • 图的遍历
        • 深度优先遍历
          • 思路
          • 邻接表
          • 邻接矩阵
          • 性能分析
        • 广度优先遍历
          • 思路
          • 邻接表
          • 邻接矩阵
          • 性能分析
        • 源代码

图的遍历

**对有向图和无向图进行遍历是按照某种次序系统地访问图中的所有顶点, 并且使得每一个顶点只能访问一次. **

对于图的遍历需要解决掉两个问题:

  1. 如果存在回路/环的图, 会陷入死循环.
  2. 对于非连通图, 从一顶点出发, 不能到达所有其它的顶点.

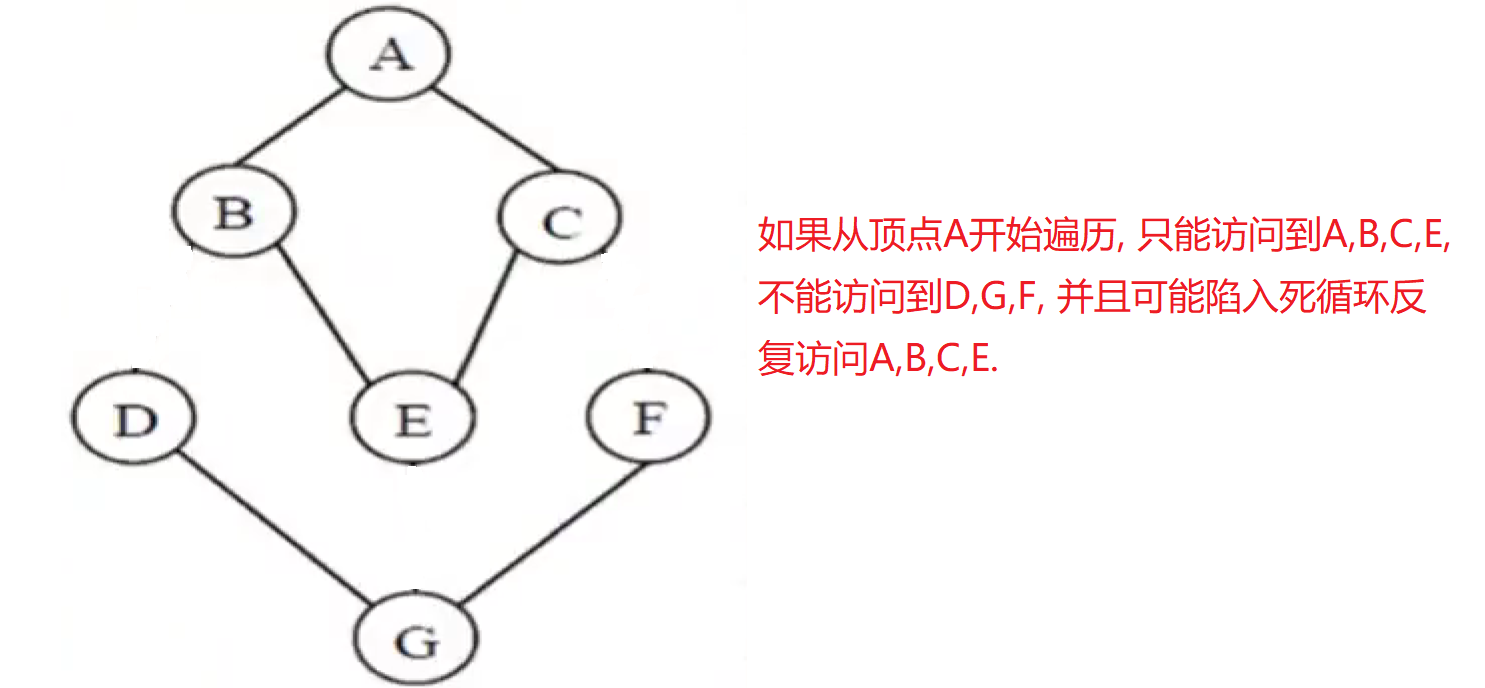
image-20230103124533746

**解决方法: **

**为每一个顶点保留一个标志位数组visited, 算法开始时, 所有顶点的标志位都置为false. **

在遍历的过程中, 当某个顶点被访问时, 其标志位就可以被标记为已访问true.

深度优先遍历

思路
  1. 首先选定一个未被访问的顶点src, 访问此顶点并作已访问标志.
  2. 然后依次从src的未被访问的邻接顶点出发进行深度优先遍历图.
  3. 重复上述过程直至图中所有和src有路径想通的顶点都被访问到.
  4. 如果还有顶点未被访问, 再选取其它未被访问的顶点, 重复以上遍历过程, 直到图中所有的顶点都被访问过.

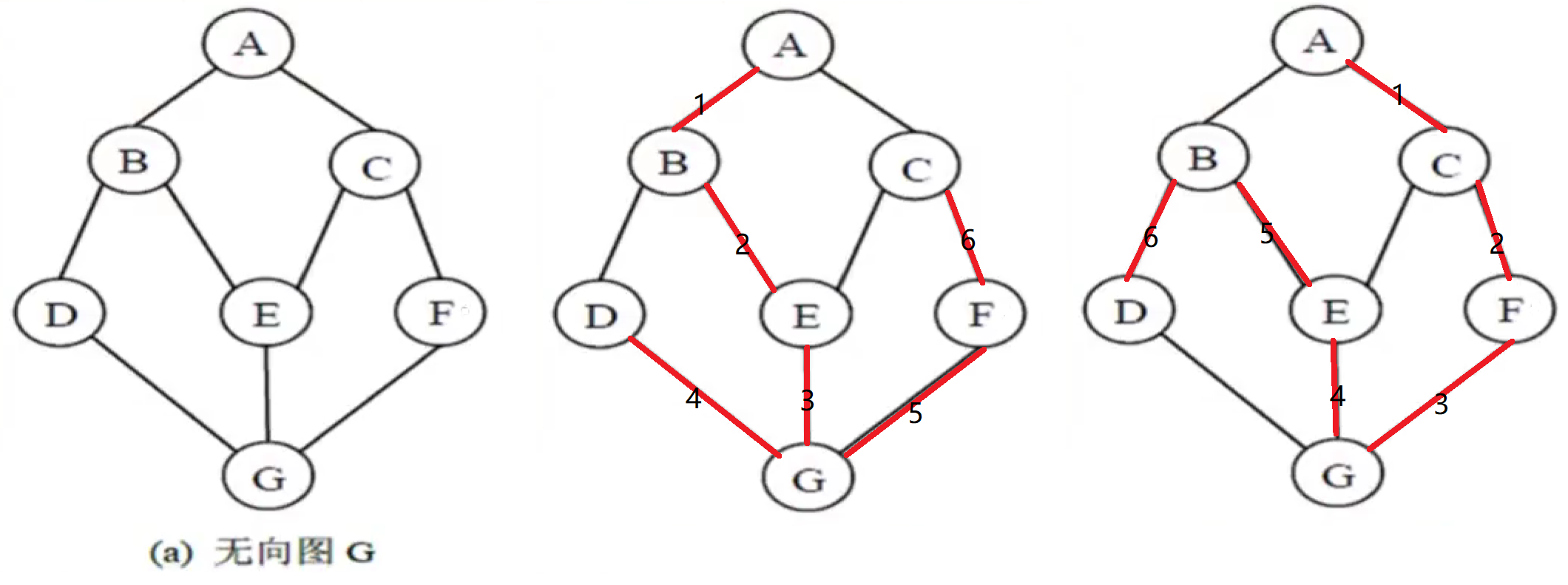
image-20230103130301425

无向图G, 从顶点A出发, 一种可能的深度优先遍历: A,B,E,G,D,F,C. 另一种可能的深度优先遍历: A,C,F,G,E,B,D. 所以当存储结构和遍历算法不确定时, 其遍历结果可能不唯一.

邻接表
namespace AdjacentList
{
	template<typename W>
	struct Edge
	{
		int _dsti;
		W _weight;

		struct Edge<W>* _next;

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			, _weight(weight)
			, _next(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度边表
    }
}

image-20230103131244934

邻接矩阵
namespace AdjacentMatrix
{
	template<typename V, typename W, W W_MAX, bool Directed = false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
    }
}

image-20230103131534639

性能分析

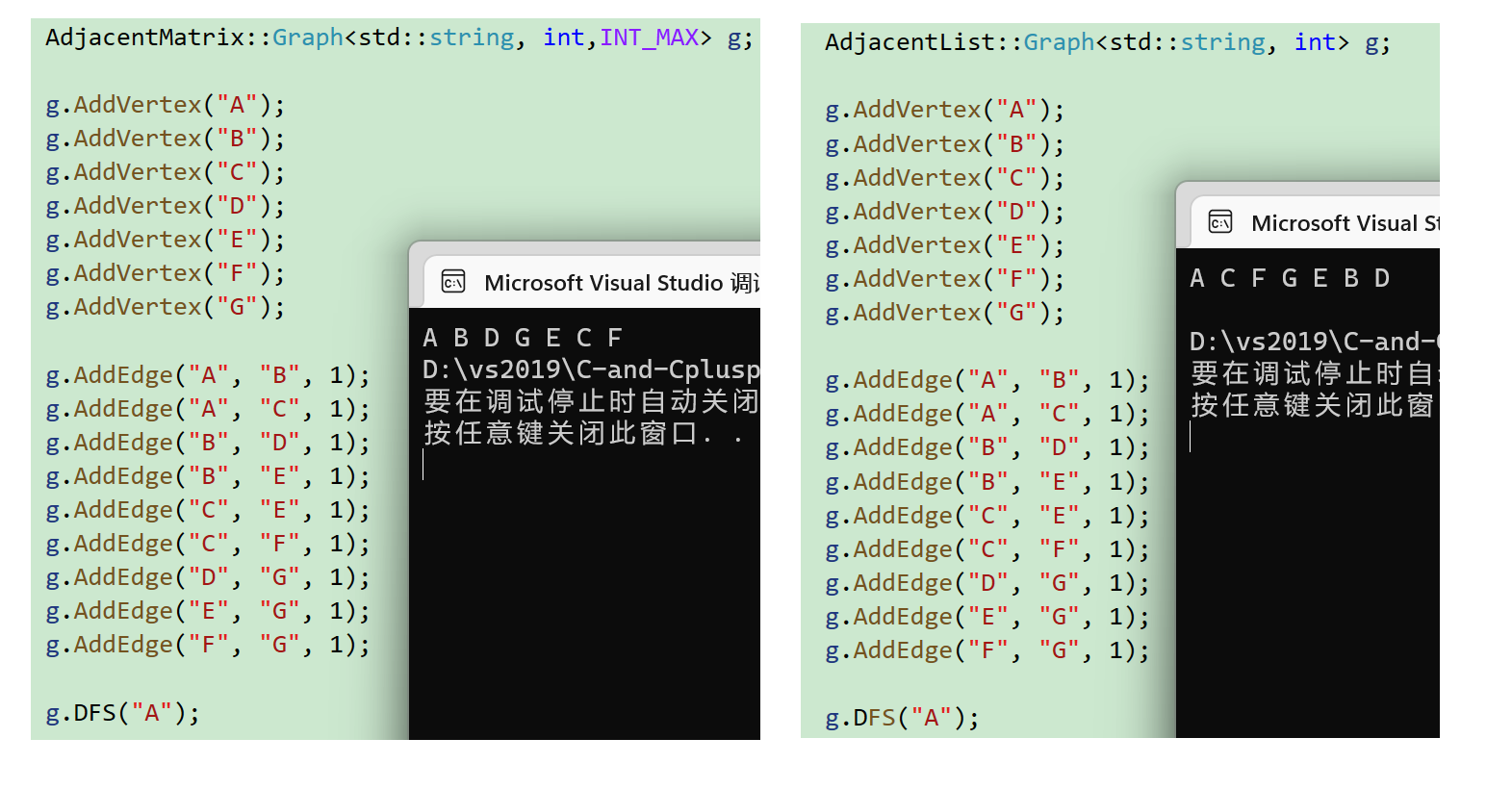
**设图G有n个顶点, e条边, 深度优先遍历算法将对图中所有的顶点和边进行访问, 因此它的时间代价和顶点数n及边弧数e是相关联的. **

若采用邻接表实现, 算法的时间复杂度为O(n+e).

若采用邻接矩阵实现, 算法的时间复杂度为O(n2).

image-20230103181306444

广度优先遍历

思路

图的广度优先遍历类似树的层次遍历, 算法思想如下:

  1. 首先选定一个未被访问过的顶点src, 访问此顶点并作已访问标志.
  2. 然后依次访问与顶点src邻接的未被访问的全部邻接点, 然后从这些访问过的邻接点出发依次访问它们各自未被访问的邻接点, 并使"先被访问的顶点的邻接点"先于"后被访问的顶点的邻接点"被访问.
  3. 重复上述过程, 直至图中所有与顶点src有路径相连的顶点都被访问到.
  4. 若图中还有其他顶点未访问到, 则任选其中一个做源点, 继续进行广度优先遍历搜索, 直到访问完图中的所有顶点为止.

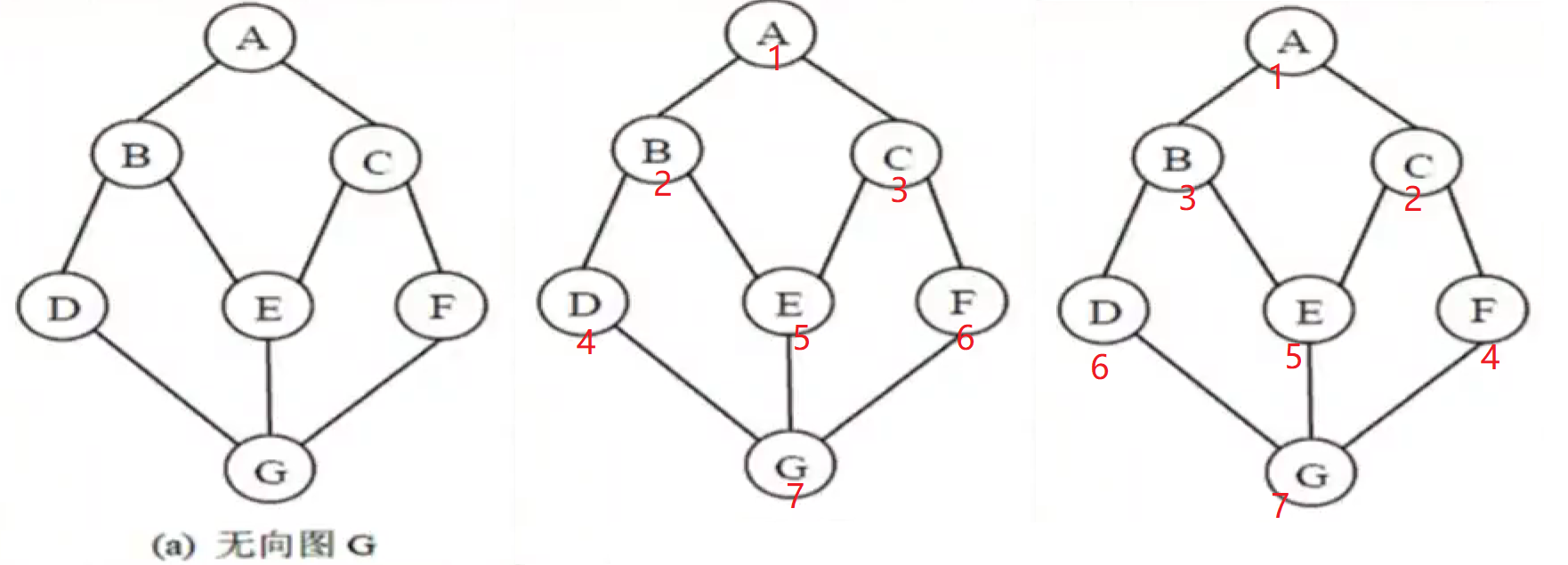
image-20230103170257332

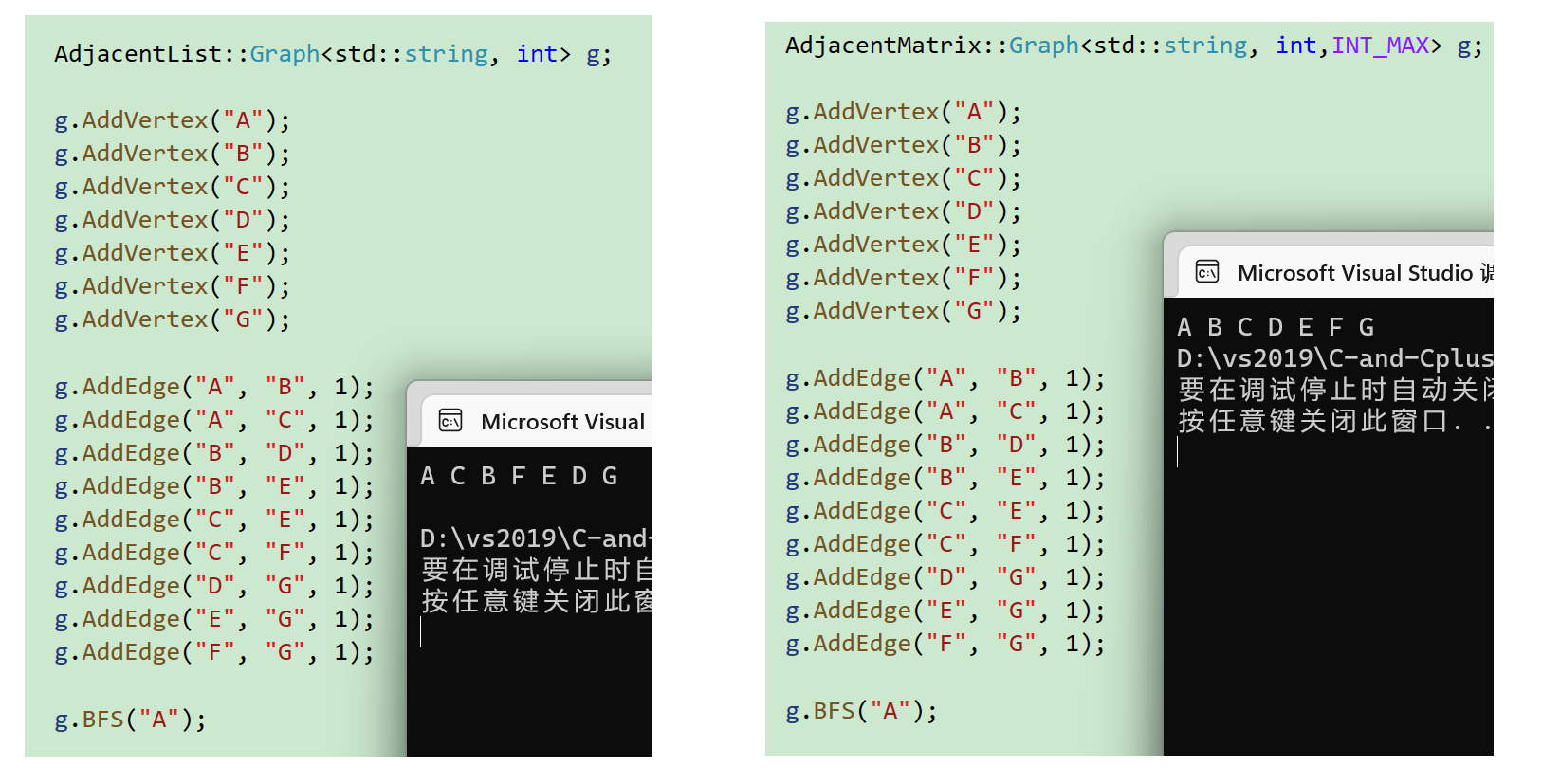
从顶点A出发一种可能的广度优先遍历序列: A,B,C,D,E,F,G.

从顶点A出发的另一种可能的广度优先遍历序列: A,C,B,F,E,D,G.

  • 那么, 怎样才能实现如步骤2所指定的顶点的访问顺序呢?

  • 这就需要借助队列来存放顶点的邻接点.

  1. 先将遍历的起始源点入队, 然后标记该顶点被访问过.
  2. 在队列不为空的情况下, 反复进行如下操作: 队头元素出队, 访问该队头元素顶点, 然后将该队头元素顶点的未被访问的邻接点入队, 并标记入队的顶点被访问过.直至队列为空.
  3. 如果图中还有未被访问的顶点, 说明图不是连通图, 则需要再选择任一未被访问过的顶点, 重复上述过程, 直到所有顶点都被访问过.

image-20230103183208730

邻接表

image-20230103173527359

邻接矩阵

image-20230103173832469

性能分析

**设图G有n个顶点, e条边, 在广度优先遍历算法中, 每一个顶点都会进一次队列且只进一次, 同时每次要遍历每个顶点对应的链表中所有边表顶点一次, 因此若采用邻接表作为存储结构, 广度优先遍历的时间为O(n+e).若采用邻接矩阵作为存储结构, 则时间为O(n2), 而空间复杂度均为O(n). **

image-20230103181030111

源代码

namespace AdjacentMatrix
{
	template<typename V, typename W, W W_MAX, bool Directed = false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
	public:

		Graph() = default;

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			// 顶点存在不需要继续增加
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);
			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			// 先在原有的行上一列
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].push_back(W_MAX);
			}

			// 增加一行
			_matrix.push_back(std::vector<W>(_vertexSet.size(), W_MAX));

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			_matrix[srci][dsti] = weight;

			// 如果为无向图,则需要再添加一条dst->src的边
			if (!Directed)
			{
				_matrix[dsti][srci] = weight;
			}

			return true;
		}

		void _BFS(int srci,vector<bool>& visited)
		{
			queue<int> q;
			q.push(srci);
			visited[srci] = true;

			while (!q.empty())
			{
				auto front = q.front();
				q.pop();

				std::cout << _vertexSet[front] << " ";

				for (int i = 0; i < static_cast<int>(_vertexSet.size()); i++)
				{
					if (_matrix[front][i] != W_MAX && !visited[i])
					{
						q.push(i);
						visited[i] = true;
					}
				}
			}
		}

		// 广度优先遍历
		void BFS(const V& src)
		{
			int srci = GetVertexIndex(src);

			// 遍历源点不存在,不能进行遍历
			if (srci == -1)
			{
				printf("输入的遍历源点不存在\n");
				return;
			}

			vector<bool> visited(_vertexSet.size(), false);

			_BFS(srci, visited);

			// 避免非连通图的出现
			for (int i = 0; i < static_cast<int>(_vertexSet.size()); i++)
			{
				if (!visited[i])
				{
					_BFS(i, visited);
				}
			}
		}

		void _DFS(int srci, vector<bool>& visited)
		{
			std::cout << _vertexSet[srci] << " ";
			visited[srci] = true;

			for (int i = 0; i < static_cast<int>(_vertexSet.size()); i++)
			{
				if (_matrix[srci][i] != W_MAX && !visited[i])
				{
					_DFS(i, visited);
				}
			}
		}

		// 深度优先遍历
		void DFS(const V& src)
		{
			int srci = GetVertexIndex(src);

			// 遍历源点不存在,不能进行遍历
			if (srci == -1)
			{
				printf("输入的遍历源点不存在\n");
				return;
			}

			vector<bool> visited(_vertexSet.size(), false);

			_DFS(srci, visited);

			for (int i = 0; i < static_cast<int>(_vertexSet.size()); i++)
			{
				if (!visited[i])
				{
					_DFS(i, visited);
				}
			}
		}
	};
}

int main(int, char**, char**)
{
	AdjacentMatrix::Graph<std::string, int,INT_MAX> g;

	g.AddVertex("A");
	g.AddVertex("B");
	g.AddVertex("C");
	g.AddVertex("D");
	g.AddVertex("E");
	g.AddVertex("F");
	g.AddVertex("G");

	g.AddEdge("A", "B", 1);
	g.AddEdge("A", "C", 1);
	g.AddEdge("B", "D", 1);
	g.AddEdge("B", "E", 1);
	g.AddEdge("C", "E", 1);
	g.AddEdge("C", "F", 1);
	g.AddEdge("D", "G", 1);
	g.AddEdge("E", "G", 1);
	g.AddEdge("F", "G", 1);

	g.DFS("A");
    g.BFS("A");

	return 0;
}

namespace AdjacentList
{
	template<typename W>
	struct Edge
	{
		int _dsti;
		W _weight;

		struct Edge<W>* _next;

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			, _weight(weight)
			, _next(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度边表
	public:
		Graph() = default;

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);

			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			_table.push_back(nullptr);

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			Edge* edge = new Edge(dsti, weight);

			// 头插
			edge->_next = _table[srci];
			_table[srci] = edge;

			// 无向图
			if (!Directed)
			{
				edge = new Edge(srci, weight);

				edge->_next = _table[dsti];
				_table[dsti] = edge;
			}

			return true;
		}

		void _DFS(int srci, vector<bool>& visited)
		{
			// 访问并标记已经访问过
			std::cout << _vertexSet[srci] << " ";
			visited[srci] = true;

			// 遍历与顶点src相连的顶点
			Edge* curr = _table[srci];
			while (curr != nullptr)
			{
				// 只有与src相连并且没有被访问过的顶点才可以进行访问
				if (!visited[curr->_dsti])
				{
					_DFS(curr->_dsti, visited);
				}
				curr = curr->_next;
			}
		}

		// 深度优先遍历
		void DFS(const V& src)
		{
			// err:
			/*static const int N = _vertexSet.size();
			bitset<_vertexSet.size()> bitMap;*/

			// 标记顶点是否被访问过 
			vector<bool> visited(_vertexSet.size(),false);

			this->_DFS(GetVertexIndex(src), visited);

			// 检查是否还有顶点没有遍历过
			for (int i = 0; i < static_cast<int>(visited.size()); i++)
			{
				if (!visited[i])
				{
					_DFS(i, visited);
				}
			}

			std::cout << std::endl;
		}
		
		void _BFS(int srci, vector<bool>& visited)
		{
			queue<int> q;
			// 只要入进队列了就可以标记访问过
			q.push(srci);
			visited[srci] = true;

			while (!q.empty())
			{
				auto front = q.front();
				q.pop();

				std::cout << _vertexSet[front] << " ";

				// 遍历与src顶点相连的边
				Edge* curr = _table[front];
				while (curr != nullptr)
				{
					// 只有与src相连并且没有被访问过的顶点才可以进行访问
					if (!visited[curr->_dsti])
					{
						q.push(curr->_dsti);
						visited[curr->_dsti] = true;
					}
					curr = curr->_next;
				}
			}
		}

		// 广度优先遍历
		void BFS(const V& src)
		{
			vector<bool> visited(_vertexSet.size(), false);

			_BFS(GetVertexIndex(src), visited);

			// 检查是否还有顶点没有遍历过
			for (int i = 0; i < static_cast<int>(visited.size()); i++)
			{
				if (!visited[i])
				{
					_BFS(i, visited);
				}
			}

			std::cout << std::endl;
		}
	};
}

int main(int, char**, char**)
{
	AdjacentList::Graph<std::string, int> g;
	
	g.AddVertex("A");
	g.AddVertex("B");
	g.AddVertex("C");
	g.AddVertex("D");
	g.AddVertex("E");
	g.AddVertex("F");
	g.AddVertex("G");

	g.AddEdge("A", "B", 1);
	g.AddEdge("A", "C", 1);
	g.AddEdge("B", "D", 1);
	g.AddEdge("B", "E", 1);
	g.AddEdge("C", "E", 1);
	g.AddEdge("C", "F", 1);
	g.AddEdge("D", "G", 1);
	g.AddEdge("E", "G", 1);
	g.AddEdge("F", "G", 1);

	g.DFS("A");
	g.BFS("A");

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/136471.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

实力总结四类Bean注入Spring的方式

实力总结四类Bean注入Spring的方式

xml 方式 注解方式 Configuration Bean Import FactoryBean BDRegistryPostProcessor 源码 实战 一提到Spring&#xff0c;大家最先想到的是啥&#xff1f;是AOP和IOC的两大特性&#xff1f;是Spring中Bean的初始化流程&#xff1f;还是基于Spring的Spring Cloud全家桶呢…
阅读更多...
Vue组件之间的通信

Vue组件之间的通信

1、组件&#xff1a;是vue的重要的特征之一&#xff0c;可以扩展html的功能&#xff0c;也可以封装代码实现重复使用 2、组件的创建 &#xff08;1&#xff09;非脚手架方式创建&#xff1a; 1️⃣使用vue.extend创建组件 2️⃣使用vue.component注册组件 3️⃣在html页面…
阅读更多...
一个平凡打工人在 CSDN 的 2022 与 2023

一个平凡打工人在 CSDN 的 2022 与 2023

平凡又不平凡的一年 2022 年是不平凡的一年&#xff0c;这一年经历了疫情的起起伏伏&#xff0c;随着身边好多同学的毕业离开&#xff0c;手头的工作也愈发的繁重&#xff0c;2022 年也顺理成章的成为了工作3年来最忙碌的一年&#xff0c;但却也是博客产出与自己收获最多的一年…
阅读更多...
大数据hadoop和spark怎么选择?

大数据hadoop和spark怎么选择?

Hadoop框架的主要模块包括如下&#xff1a; Hadoop Common Hadoop分布式文件系统(HDFS) Hadoop YARN Hadoop MapReduce 虽然上述四个模块构成了Hadoop的核心&#xff0c;不过还有其他几个模块。这些模块包括&#xff1a;Ambari、Avro、Cassandra、Hive、 Pig、Oozie、Flume…
阅读更多...
spring之静态代理

spring之静态代理

文章目录前言一、代理模式中的三大角色二、静态代理引入1.业务接口2.目标对象总结前言 在Java程序中代理模式的作用&#xff1a; 当一个对象需要收到保护的时候可以考虑使用代理对象去完成某个行为需要给某个对象的功能进行功能增强的时候&#xff0c;可以考虑找一个代理进行…
阅读更多...
Java内存模型(JMM)详解！

Java内存模型(JMM)详解！

文章目录什么是JMM?现代计算机内存模型缓存一致性JMM内存模型与计算机内存模型的关系线程间通信JMM三大问题原子性可见性有序性什么是JMM? JMM定义了Java 虚拟机(JVM)在计算机内存(RAM)中的工作方式。 JMM可以理解为是一个规范&#xff0c;一个抽象概念&#xff0c;并不真实…
阅读更多...
Java 单元测试

Java 单元测试

目录 一、Junit 1.1、单元测试初始化与清理资源 1.2、捕获异常 1.3、条件测试 1.4、标记失效测试方法 1.5、参数化测试 单元测试&#xff1a;是对最小功能单元编写的测试代码。 示例&#xff0c;当开发好一个 Java 阶乘的方法。 n&#xff01; 1 x 2 x 3 x ..…
阅读更多...
CRM软件哪个好？该如何选择？

CRM软件哪个好？该如何选择？

CRM软件哪个好&#xff1f;该如何选择&#xff1f; CRM是集营销、销售、服务为一体的围绕客户全生命周期管理的系统&#xff0c;在各行各业的数字化转型大潮中&#xff0c;作为以消费者、终端用户、客户为主导的企业经营管理核心系统&#xff0c;CRM选型的难度和复杂度也在不断…
阅读更多...
关于ETL的两种架构（ETL架构和ELT架构）

关于ETL的两种架构（ETL架构和ELT架构）

ETL&#xff0c;是英文 Extract-Transform-Load 的缩写&#xff0c;用来描述将数据从来源端经过抽取&#xff08;extract&#xff09;、转换&#xff08;transform&#xff09;、加载&#xff08;load&#xff09;至目的端的过程。ETL一词较常用在数据仓库&#xff0c;但其对象…
阅读更多...
Java的JVM垃圾回收机制GC概述

Java的JVM垃圾回收机制GC概述

JVM——GC机制1、什么是GC&#xff1f;2、GC算法的总体概述3、JVM所处的位置4、JVM整体结构5、JVM架构模型6、Java垃圾回收机制优缺点7、GC主要关注的区域垃圾回收算法&#xff1a;标记阶段&#xff0c;引用计数循环引用标记阶段&#xff1a;可达性分析算法GC root可以是哪些&a…
阅读更多...
JavaScript代码题--以及一些奇奇怪怪的发现

JavaScript代码题--以及一些奇奇怪怪的发现

解析 let a{b:10,c:{d:[11,12],e:13}}&#xff0c;实现 10111213 效果 解 const a{b:10,c:{d:[11,12],e:13}}function sum(obj) {let total 0;const value Object.values(obj)value.forEach(item>{total typeof item number ? item : sum(item)})return total }const …
阅读更多...
Java家教系统家教网站家教兼职系统

Java家教系统家教网站家教兼职系统

简介&#xff1a; 用户可以注册成为学员也可以是教员。教员发布家教信息&#xff0c;学员根据自己的要求查找符合自己的教员。学员预约教员的某一天去家教&#xff0c;教员可以在个人中心里查看&#xff0c;是否接受该预约。在教员接受或拒绝之前&#xff0c;学员随时可以取消…
阅读更多...
数据库，计算机网络、操作系统刷题笔记23

数据库，计算机网络、操作系统刷题笔记23

数据库&#xff0c;计算机网络、操作系统刷题笔记23 2022找工作是学历、能力和运气的超强结合体&#xff0c;遇到寒冬&#xff0c;大厂不招人&#xff0c;可能很多算法学生都得去找开发&#xff0c;测开 测开的话&#xff0c;你就得学数据库&#xff0c;sql&#xff0c;oracle…
阅读更多...
基于 Vue 制作一个猜拳小游戏

基于 Vue 制作一个猜拳小游戏

目录前言&#xff1a;项目效果展示&#xff1a;对应素材&#xff1a;代码实现思路&#xff1a;实现代码&#xff1a;总结&#xff1a;前言&#xff1a; 在工作学习之余玩一会游戏既能带来快乐&#xff0c;还能缓解生活压力&#xff0c;跟随此文一起制作一个小游戏吧。 描述&…
阅读更多...
【2042. 检查句子中的数字是否递增】

【2042. 检查句子中的数字是否递增】

来源&#xff1a;力扣&#xff08;LeetCode&#xff09; 描述&#xff1a; 句子是由若干 token 组成的一个列表&#xff0c;token 间用 单个 空格分隔&#xff0c;句子没有前导或尾随空格。每个 token 要么是一个由数字 0-9 组成的不含前导零的 正整数 &#xff0c;要么是一个…
阅读更多...
ORA-00600 kcratr_nab_less_than_odr 问题处理

ORA-00600 kcratr_nab_less_than_odr 问题处理

问题&#xff1a;ORA-00600: 内部错误代码, 参数: [kcratr_nab_less_than_odr], [1], [196495], [39399], [39460], [], [], [], [], [], [], []导致原因&#xff1a;可能是由于服务器宕机&#xff0c;控制文件的缺失&#xff0c;或者在线日志文件在实例恢复时不完整1、数据库未…
阅读更多...
5G边缘计算网关助力5G工业物联网智能化建设

5G边缘计算网关助力5G工业物联网智能化建设

5G边缘计算&#xff0c;凭借高带宽、高可靠、低时延、移动性等特性&#xff0c;推动工业生产物联网发展趋势&#xff0c;实现工业更快、更精准通信及数据共享。边缘计算网关下5G工业物联网远程感知生产一线&#xff0c;工控数字化、自动化、智能化&#xff0c;降低人物力资源成…
阅读更多...
LeetCode 2042. 检查句子中的数字是否递增

LeetCode 2042. 检查句子中的数字是否递增

【LetMeFly】2042.检查句子中的数字是否递增 力扣题目链接&#xff1a;https://leetcode.cn/problems/check-if-numbers-are-ascending-in-a-sentence/ 句子是由若干 token 组成的一个列表&#xff0c;token 间用 单个 空格分隔&#xff0c;句子没有前导或尾随空格。每个 tok…
阅读更多...
【计算机体系结构】指令集并行（ILP）动态调度算法：Tomasulo实现代码（Tomasulo Algorithm Implementation）

【计算机体系结构】指令集并行（ILP）动态调度算法：Tomasulo实现代码（Tomasulo Algorithm Implementation）

Tomasulo Algorithm Implementation &#xff08;本文章仅提供算法实现过程&#xff0c;具体算法思想请查阅教科书&#xff09; 如果觉得这篇文章有用&#xff0c;请记得点个赞并收藏哦&#xff01; 1.Introduction Tomasulo算法用于指令的动态调度&#xff0c;允许乱序执行…
阅读更多...
C C++内存对齐以及特殊类的大小

C C++内存对齐以及特殊类的大小

目录C语言内存对齐现象内存对齐规则为什么存在内存对齐如果struct or class中存在成员函数时的大小空类大小为1Cclass存在虚函数时的大小C语言 内存对齐现象 C语言中结构体的大小往往不是结构体中各种数据类型的加和&#xff0c;因为存在内存对齐; struct S {double d;//8字…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023