深层神经网络
前面一章我们简要介绍了神经网络的一些基本知识,同时也是示范了如何用神经网络构建一个复杂的非线性二分类器,更多的情况神经网络适合使用在更加复杂的情况,比如图像分类的问题,下面我们用深度学习的入门级数据集 MNIST 手写体分类来说明一下更深层神经网络的优良表现。
这里其实最有用的是看最后的画图是怎么画的。这里有篇文章:十分钟搞懂Pytorch如何读取MNIST数据集
MNIST 数据集
mnist 数据集是一个非常出名的数据集,基本上很多网络都将其作为一个测试的标准,其来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST)。 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员,一共有 60000 张图片。 测试集(test set) 也是同样比例的手写数字数据,一共有 10000 张图片。
每张图片大小是 28 x 28 的灰度图,如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ng8CYPRd-1672557766736)(null)]
所以我们的任务就是给出一张图片,我们希望区别出其到底属于 0 到 9 这 10 个数字中的哪一个。
多分类问题
前面我们讲过二分类问题,现在处理的问题更加复杂,是一个 10 分类问题,统称为多分类问题,对于多分类问题而言,我们的 loss 函数使用一个更加复杂的函数,叫交叉熵。
softmax
提到交叉熵,我们先讲一下 softmax 函数,前面我们见过了 sigmoid 函数,如下
s ( x ) = 1 1 + e − x s(x) = \frac{1}{1 + e^{-x}} s(x)=1+e−x1
可以将任何一个值转换到 0 ~ 1 之间,当然对于一个二分类问题,这样就足够了,因为对于二分类问题,如果不属于第一类,那么必定属于第二类,所以只需要用一个值来表示其属于其中一类概率,但是对于多分类问题,这样并不行,需要知道其属于每一类的概率,这个时候就需要 softmax 函数了。
softmax 函数示例如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-I5UEmkTm-1672557766723)(null)]
对于网络的输出 z 1 , z 2 , ⋯ z k z_1, z_2, \cdots z_k z1,z2,⋯zk,我们首先对他们每个都取指数变成 e z 1 , e z 2 , ⋯ , e z k e^{z_1}, e^{z_2}, \cdots, e^{z_k} ez1,ez2,⋯,ezk,那么每一项都除以他们的求和,也就是
z i → e z i ∑ j = 1 k e z j z_i \rightarrow \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}} zi→∑j=1kezjezi
如果对经过 softmax 函数的所有项求和就等于 1,所以他们每一项都分别表示属于其中某一类的概率。
交叉熵
交叉熵衡量两个分布相似性的一种度量方式,前面讲的二分类问题的 loss 函数就是交叉熵的一种特殊情况,交叉熵的一般公式为
c r o s s _ e n t r o p y ( p , q ) = E p [ − log q ] = − 1 m ∑ x p ( x ) log q ( x ) cross\_entropy(p, q) = E_{p}[-\log q] = - \frac{1}{m} \sum_{x} p(x) \log q(x) cross_entropy(p,q)=Ep[−logq]=−m1x∑p(x)logq(x)
对于二分类问题我们可以写成
− 1 m ∑ i = 1 m ( y i log s i g m o i d ( x i ) + ( 1 − y i ) log ( 1 − s i g m o i d ( x i ) ) -\frac{1}{m} \sum_{i=1}^m (y^{i} \log sigmoid(x^{i}) + (1 - y^{i}) \log (1 - sigmoid(x^{i})) −m1i=1∑m(yilogsigmoid(xi)+(1−yi)log(1−sigmoid(xi))
这就是我们之前讲的二分类问题的 loss,当时我们并没有解释原因,只是给出了公式,然后解释了其合理性,现在我们给出了公式去证明这样取 loss 函数是合理的
交叉熵是信息理论里面的内容,这里不再具体展开,更多的内容,可以看到下面的链接
下面我们直接用 mnist 举例,讲一讲深度神经网络
import numpy as np
import torch
from torchvision.datasets import mnist # 导入 pytorch 内置的 mnist 数据
from torch import nn
from torch.autograd import Variable
# 使用内置函数下载 mnist 数据集
train_set = mnist.MNIST('./data', train=True, download=True)
test_set = mnist.MNIST('./data', train=False, download=True)
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Processing...
Done!
我们可以看看其中的一个数据是什么样子的
a_data, a_label = train_set[0]
a_data

a_label
5
这里的读入的数据是 PIL 库中的格式,我们可以非常方便地将其转换为 numpy array
a_data = np.array(a_data, dtype='float32')
print(a_data.shape)
(28, 28)
这里我们可以看到这种图片的大小是 28 x 28
print(a_data)
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 3. 18.
18. 18. 126. 136. 175. 26. 166. 255. 247. 127. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 30. 36. 94. 154. 170. 253.
253. 253. 253. 253. 225. 172. 253. 242. 195. 64. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 49. 238. 253. 253. 253. 253. 253.
253. 253. 253. 251. 93. 82. 82. 56. 39. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 18. 219. 253. 253. 253. 253. 253.
198. 182. 247. 241. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 80. 156. 107. 253. 253. 205.
11. 0. 43. 154. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 14. 1. 154. 253. 90.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 139. 253. 190.
2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 11. 190. 253.
70. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 35. 241.
225. 160. 108. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 81.
240. 253. 253. 119. 25. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
45. 186. 253. 253. 150. 27. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 16. 93. 252. 253. 187. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 249. 253. 249. 64. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
46. 130. 183. 253. 253. 207. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 39. 148.
229. 253. 253. 253. 250. 182. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 24. 114. 221. 253.
253. 253. 253. 201. 78. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 23. 66. 213. 253. 253. 253.
253. 198. 81. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 18. 171. 219. 253. 253. 253. 253. 195.
80. 9. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 55. 172. 226. 253. 253. 253. 253. 244. 133. 11.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 136. 253. 253. 253. 212. 135. 132. 16. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
我们可以将数组展示出来,里面的 0 就表示黑色,255 表示白色
对于神经网络,我们第一层的输入就是 28 x 28 = 784,所以必须将得到的数据我们做一个变换,使用 reshape 将他们拉平成一个一维向量
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化,这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x
train_set = mnist.MNIST('./data', train=True, transform=data_tf, download=True) # 重新载入数据集,申明定义的数据变换
test_set = mnist.MNIST('./data', train=False, transform=data_tf, download=True)
a, a_label = train_set[0]
print(a.shape)
print(a_label)
torch.Size([784])
5
from torch.utils.data import DataLoader
# 使用 pytorch 自带的 DataLoader 定义一个数据迭代器
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
test_data = DataLoader(test_set, batch_size=128, shuffle=False)
使用这样的数据迭代器是非常有必要的,如果数据量太大,就无法一次将他们全部读入内存,所以需要使用 python 迭代器,每次生成一个批次的数据
a, a_label = next(iter(train_data))
# 打印出一个批次的数据大小
print(a.shape)
print(a_label.shape)
torch.Size([64, 784])
torch.Size([64])
# 使用 Sequential 定义 4 层神经网络
net = nn.Sequential(
nn.Linear(784, 400),
nn.ReLU(),
nn.Linear(400, 200),
nn.ReLU(),
nn.Linear(200, 100),
nn.ReLU(),
nn.Linear(100, 10)
)
net
Sequential(
(0): Linear(in_features=784, out_features=400)
(1): ReLU()
(2): Linear(in_features=400, out_features=200)
(3): ReLU()
(4): Linear(in_features=200, out_features=100)
(5): ReLU()
(6): Linear(in_features=100, out_features=10)
)
交叉熵在 pytorch 中已经内置了,交叉熵的数值稳定性更差,所以内置的函数已经帮我们解决了这个问题
# 定义 loss 函数
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), 1e-1) # 使用随机梯度下降,学习率 0.1
# 开始训练
losses = []
acces = []
eval_losses = []
eval_acces = []
for e in range(20):
train_loss = 0
train_acc = 0
net.train()
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.item()
# 计算分类的准确率
_, pred = out.max(1)
num_correct = (pred == label).sum().item()
acc = num_correct / im.shape[0]
train_acc += acc
losses.append(train_loss / len(train_data))
acces.append(train_acc / len(train_data))
# 在测试集上检验效果
eval_loss = 0
eval_acc = 0
net.eval() # 将模型改为预测模式
for im, label in test_data:
im = Variable(im)
label = Variable(label)
out = net(im)
loss = criterion(out, label)
# 记录误差
eval_loss += loss.item()
# 记录准确率
_, pred = out.max(1)
num_correct = (pred == label).sum().item()
acc = num_correct / im.shape[0]
eval_acc += acc
eval_losses.append(eval_loss / len(test_data))
eval_acces.append(eval_acc / len(test_data))
print('epoch: {}, Train Loss: {:.6f}, Train Acc: {:.6f}, Eval Loss: {:.6f}, Eval Acc: {:.6f}'
.format(e, train_loss / len(train_data), train_acc / len(train_data),
eval_loss / len(test_data), eval_acc / len(test_data)))
epoch: 0, Train Loss: 0.525527, Train Acc: 0.830690, Eval Loss: 0.214004, Eval Acc: 0.929292
epoch: 1, Train Loss: 0.169223, Train Acc: 0.948527, Eval Loss: 0.156571, Eval Acc: 0.951048
epoch: 2, Train Loss: 0.119509, Train Acc: 0.962537, Eval Loss: 0.141246, Eval Acc: 0.955301
epoch: 3, Train Loss: 0.093633, Train Acc: 0.970349, Eval Loss: 0.096926, Eval Acc: 0.970036
epoch: 4, Train Loss: 0.077827, Train Acc: 0.975413, Eval Loss: 0.088236, Eval Acc: 0.971025
epoch: 5, Train Loss: 0.062835, Train Acc: 0.980211, Eval Loss: 0.090155, Eval Acc: 0.973200
epoch: 6, Train Loss: 0.053678, Train Acc: 0.983109, Eval Loss: 0.084136, Eval Acc: 0.974189
epoch: 7, Train Loss: 0.056607, Train Acc: 0.982343, Eval Loss: 0.075727, Eval Acc: 0.976562
epoch: 8, Train Loss: 0.040552, Train Acc: 0.986774, Eval Loss: 0.065600, Eval Acc: 0.980024
epoch: 9, Train Loss: 0.034272, Train Acc: 0.989272, Eval Loss: 0.121962, Eval Acc: 0.963212
epoch: 10, Train Loss: 0.030490, Train Acc: 0.990005, Eval Loss: 0.067141, Eval Acc: 0.979233
epoch: 11, Train Loss: 0.027200, Train Acc: 0.991188, Eval Loss: 0.160441, Eval Acc: 0.953521
epoch: 12, Train Loss: 0.023948, Train Acc: 0.991904, Eval Loss: 0.076049, Eval Acc: 0.980123
epoch: 13, Train Loss: 0.018909, Train Acc: 0.993503, Eval Loss: 0.065272, Eval Acc: 0.980518
epoch: 14, Train Loss: 0.017229, Train Acc: 0.994386, Eval Loss: 0.067790, Eval Acc: 0.981309
epoch: 15, Train Loss: 0.014564, Train Acc: 0.995253, Eval Loss: 0.067104, Eval Acc: 0.981804
epoch: 16, Train Loss: 0.013621, Train Acc: 0.995819, Eval Loss: 0.076764, Eval Acc: 0.980716
epoch: 17, Train Loss: 0.012969, Train Acc: 0.995836, Eval Loss: 0.154731, Eval Acc: 0.963805
epoch: 18, Train Loss: 0.012531, Train Acc: 0.996202, Eval Loss: 0.098053, Eval Acc: 0.975574
epoch: 19, Train Loss: 0.010139, Train Acc: 0.996635, Eval Loss: 0.072089, Eval Acc: 0.982002
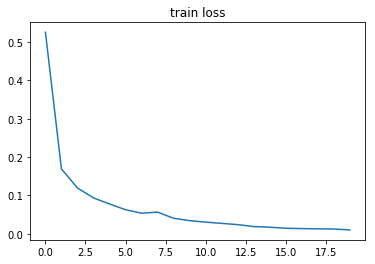
画出 loss 曲线和 准确率曲线
import matplotlib.pyplot as plt
%matplotlib inline
plt.title('train loss')
plt.plot(np.arange(len(losses)), losses)
[<matplotlib.lines.Line2D at 0x1132fb390>]
plt.plot(np.arange(len(acces)), acces)
plt.title('train acc')
<matplotlib.text.Text at 0x1134fad68>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SHuXVo5Q-1672557764360)(output_27_1.png)]](https://img-blog.csdnimg.cn/acace5d8040c4181b9a4078de93335cc.png)
plt.plot(np.arange(len(eval_losses)), eval_losses)
plt.title('test loss')
<matplotlib.text.Text at 0x1136d2860>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-R7g7QbCx-1672557764360)(output_28_1.png)]](https://img-blog.csdnimg.cn/81d4042094cd45f8819b0fb9e40ec330.png)
plt.plot(np.arange(len(eval_acces)), eval_acces)
plt.title('test acc')
<matplotlib.text.Text at 0x1137a9828>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Tvhm2M4t-1672557764360)(output_29_1.png)]](https://img-blog.csdnimg.cn/8bb9864163a74943b4e007adefa3c205.png)
可以看到我们的三层网络在训练集上能够达到 99.9% 的准确率,测试集上能够达到 98.20% 的准确率
下面是书中的代码的一部分
import torch
from torch import nn, optim
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import datasets,transforms
# MLP
class simpleNet(nn .Module):
def __init__(self, in_dim, n_hidden_1, n_hidden_2,out_dim): # 输入的维度,第一层网络的神经单元个数,第二层网络的神经单元个数,第三层……
super (simpleNet,self).__init__()
self.layer1 = nn.Linear(in_dim, n hidden_1)
self.layer2 = nn.Linear(n_hidden_1, n_hidden_2)
self.layer3 = nn.Linear(n_hidden_2,out_dim)
def forward(self, x) :
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
return x
# 激活函数
class Activation_Net(nn.Module) :
def __init__(self, in_dim, n_hidden_1, n_hidden_2,out_dim) :
super(NeuralNetwork, self).__init__()
self.layerl = nn.Sequential(nn.Linear(in_dim, n_hidden_1),nn.ReLU(True))
self.layer2 = nn.Sequential(nn.Linear(n_hidden_1, n_hidden_2), nn.ReLU(True))
self.layer3 = nn.Sequential(nn.Linear(n_hidden_2,out_dim)) # 最后一层不能添加激活函数
# nn.Sequential()是将网络的层组合到一起
def forward(self, x) :
x = self.layerl(x)
x = self.layer2(x)
x = self.layer3(x)
return x
# 添加批标准化
class Batch Net (nn .Module) :
def __init__(self, in_dim, n_hidden_1,n_hidden_2,out_dim) :
super(Batch_Net, self).__init__()
self.layerl = nn.Sequential (nn.Linear(in_dim, n_ hidden_1),nn. BatchNormld(n_hidden_1) ,nn.ReLU(True))
self.layer2 = nn.Sequential(nn.Linear(n_hidden_1, n_hidden_2),nn.BatchNorm1d(n_ hidden_2) ,nn.ReLU(True))
self.layer3 = nn.Sequential(nn.Linear(n_hidden_2,out_dim) )
def forward(self, x) :
x = self.layerl(x)
x = self.layer2(x)
x = self.layer3(x)
return x
'''
同样使用nn. Sequential()将nn. BatchNorm1d()组合到网络层中,注意批标
准化一般放在全连接层的后面、非线性层( 激活函数)的前面。
'''
# 这次的代码多了一个批标准化