简介

       kmeans算法又名k均值算法,K-means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。
        其算法思想大致为：先从样本集中随机选取 k个样本作为簇中心，并计算所有样本与这 k个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。

 数据链接

链接：https://pan.baidu.com/s/19HaKX9T5DXxqtTApqqEO1Q 
提取码：52xx

文末有代码文件。 

引用我们需要的包 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#Plot styling
import seaborn as sns; sns.set()  
%matplotlib inline

plt.rcParams['figure.figsize'] = (16, 9)    # 图像显示大小
plt.style.use('ggplot')    # 打印样式列表

读取文件 

 dataset=pd.read_csv('CLV.csv')
 dataset.head()  #查看表头

 

dataset.describe().transpose() #查看基本状况

plot_income = sns.distplot(dataset["INCOME"]) #绘制比较直方图
plot_spend = sns.distplot(dataset["SPEND"])
plt.xlabel('Income / spend')

看出看出收入和速度的分布关系： 

 绘制箱型线与核密度图的结合：

f, axes = plt.subplots(1,2, figsize=(12,6), sharex=True, sharey=True)
v1 = sns.violinplot(data=dataset, x='INCOME', color="skyblue",ax=axes[0])
v2 = sns.violinplot(data=dataset, x='SPEND',color="lightgreen", ax=axes[1])
v1.set(xlim=(0,420))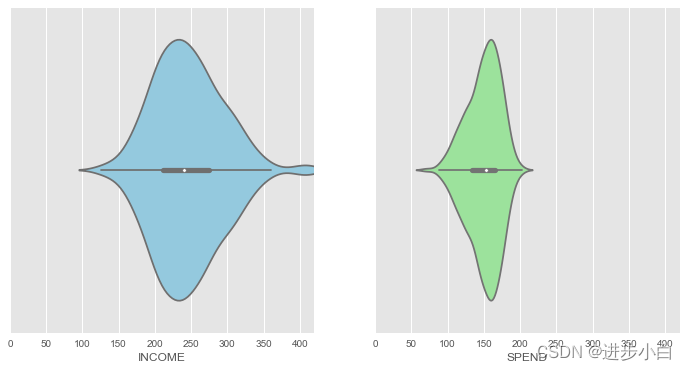

 绘制散点图

Income = dataset['INCOME'].values
Spend = dataset['SPEND'].values
X = np.array(list(zip(Income, Spend)))
plt.scatter(Income, Spend, c='black', s=100) #绘制散点图

 绘制3D图形

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1])

关于k-means的参数： 

参数	类型	解释
n_clusters	int, default=8	K-Means中的k，表示聚类数
init	{‘k-means++’, ‘random’}, default=‘k-means++’	'k-means++'用一种特殊的方法选定初始质心加速迭代过程收敛，'random’随机选取初始质心
n_init	int, default=10	用不同的聚类中心初始化值运行算法的次数，最后的解是inertial意义下选出的最优结果
max_iter	int, default=300	运行的最多迭代数
tol	float, default=1e-4	容忍的最小误差，当误差小于tol就会退出迭代
verbose	int, default=0	是否输出详细信息
random_state	int, RandomState instance or None, default=None	用于初始化质心得生成器(generator)。如果值为一个整数，则确定一个seed
copy_x	bool, default=True	如果为True，表示计算距离不会修改源数据
algorithm	{“auto”, “full”, “elkan”}, default=“auto”	优化算法，full表示一般的K-Means算法，elkan表示elkan K-Means算法，auto根据数据是否稀疏进行选择

我们选择运行最多的迭代数为300，选取运行次数为10 

from sklearn.cluster import KMeans
wcss = []
for i in range(1,11):
    km=KMeans(n_clusters=i,init='k-means++', max_iter=300, n_init=10, random_state=0)
    km.fit(X)
    wcss.append(km.inertia_)
plt.plot(range(1,11),wcss)
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('wcss')
plt.show()
    

结果如下 

 

计算轮轴系数：

轮廓系数用于计算每个样本的平均簇内距离a(样本i到同簇其他样本的平均距离，ai值越小说明该样本越应该被聚到该类，即簇内不相似度)和平均邻近簇距离b(样本i到其他相邻簇的所有样本的平均距离bi，bi越大说明样本i越不属于其他簇，即簇间不相似度)。每个样本的轮廓系数计算公式为：(b-a)/Max(a,b)，轮廓系数越接近1说明结果越好（聚类越准确），越接近-1说明结果越差，若值在0值附近，则说明样本在两个簇的边界上。 

from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans


for n_cluster in range(2, 11):
    kmeans = KMeans(n_clusters=n_cluster).fit(X)
    label = kmeans.labels_
    sil_coeff = silhouette_score(X, label, metric='euclidean')
    print("For n_clusters={}, The Silhouette Coefficient is {}".format(n_cluster, sil_coeff))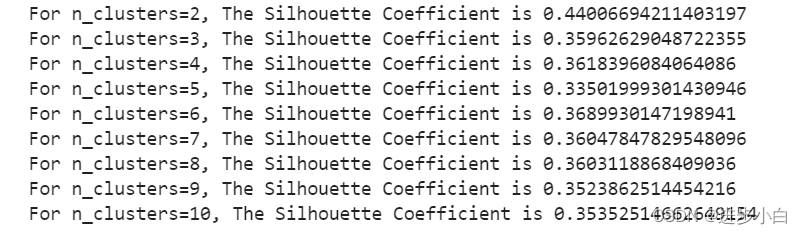

 肘部法则确定k值，score为指标

import pylab as pl
from sklearn.decomposition import PCA

Nc = range(1, 20)
kmeans = [KMeans(n_clusters=i) for i in Nc]
kmeans
score = [kmeans[i].fit(X).score(X) for i in range(len(kmeans))]
score
pl.plot(Nc,score)
pl.xlabel('Number of Clusters')
pl.ylabel('Score')
pl.title('Elbow Curve')
pl.show()

print(score)

 

 

for k in range (1, 11):
    kmeans_model = KMeans(n_clusters=k, random_state=1).fit(X)
    labels = kmeans_model.labels_    #保存标签
    interia = kmeans_model.inertia_     #保存每一个SSE的值
    print ("k:",k, " cost:", interia)
print()

 确定k为4，因为在k为4的时候，sse的变化已经缓和很多。

km4=KMeans(n_clusters=4,init='k-means++', max_iter=300, n_init=10, random_state=0)
y_means = km4.fit_predict(X)

开始聚类，配置不同的颜色。 

plt.scatter(X[y_means==0,0],X[y_means==0,1],s=50, c='purple',label='Cluster1')
plt.scatter(X[y_means==1,0],X[y_means==1,1],s=50, c='blue',label='Cluster2')
plt.scatter(X[y_means==2,0],X[y_means==2,1],s=50, c='green',label='Cluster3')
plt.scatter(X[y_means==3,0],X[y_means==3,1],s=50, c='cyan',label='Cluster4')

plt.scatter(km4.cluster_centers_[:,0], km4.cluster_centers_[:,1],s=200,marker='s', c='red', alpha=0.7, label='Centroids')
plt.title('Customer segments')
plt.xlabel('Annual income of customer')
plt.ylabel('Annual spend from customer on site')
plt.legend()
plt.show()

相关参数：

• 调用方法：plt.scatter(x, y, s, c, marker, cmap, norm, alpha, linewidths, edgecolorsl)
• 参数说明：
  • x: x轴数据
  • y: y轴数据
  • s: 散点大小
  • c: 散点颜色
  • marker: 散点形状
  • cmap: 指定特定颜色图，该参数一般不用，有默认值
  • alpha: 散点的透明度
  • linewidths: 散点边框的宽度
  • edgecolors: 设置散点边框的颜色

运行结果：

 

 

 上图可以发现，聚类的效果不是很好，接下来我们将k值定为6（0-5）：

plt.scatter(X[y_means==0,0],X[y_means==0,1],s=50, c='purple',label='Cluster1')
plt.scatter(X[y_means==1,0],X[y_means==1,1],s=50, c='blue',label='Cluster2')
plt.scatter(X[y_means==2,0],X[y_means==2,1],s=50, c='green',label='Cluster3')
plt.scatter(X[y_means==3,0],X[y_means==3,1],s=50, c='cyan',label='Cluster4')
plt.scatter(X[y_means==4,0],X[y_means==4,1],s=50, c='magenta',label='Cluster5')
plt.scatter(X[y_means==5,0],X[y_means==5,1],s=50, c='orange',label='Cluster6')

plt.scatter(km.cluster_centers_[:,0], km.cluster_centers_[:,1],s=200,marker='s', c='red', alpha=0.7, label='Centroids')
plt.title('Customer segments')
plt.xlabel('Annual income of customer')
plt.ylabel('Annual spend from customer on site')
plt.legend()
plt.show()

 

 这样结果就相对集中，效果相对较好。

在sch.dendrogram中传入一个参数sch.linkage(X, method = 'ward')，sch.linkage是数据之间的链条关系，其中的x是数据集，在进行聚类的时候，将每一个点作为一个分组，不断发现两个最近的分组，不断的进行组拼，参数method = 'ward'表示进行聚类的时候，差异最小的元素，也就是距离最近的元素，也可以使用其他的方法。在进行可视化的时候，plt自动完成了数据的显示过程。

import scipy.cluster.hierarchy as sch
dend=sch.dendrogram(sch.linkage(X, method='ward'))
plt.title("Dendrogram")
plt.xlabel('Customer')
plt.ylabel('euclidean')
plt.show()

from sklearn.cluster import AgglomerativeClustering
hc=AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward' )
y_hc = hc.fit_predict(X)

linkage 参数说明:

1. ward (默认值)：每一个类簇的方差最小化
2. average：每一个类簇之间的距离的平均值最小
3. complete：每一个类簇之间的距离最大
4. single：每一个类簇之间的距离最小

  

 完整代码参考公众号获取。