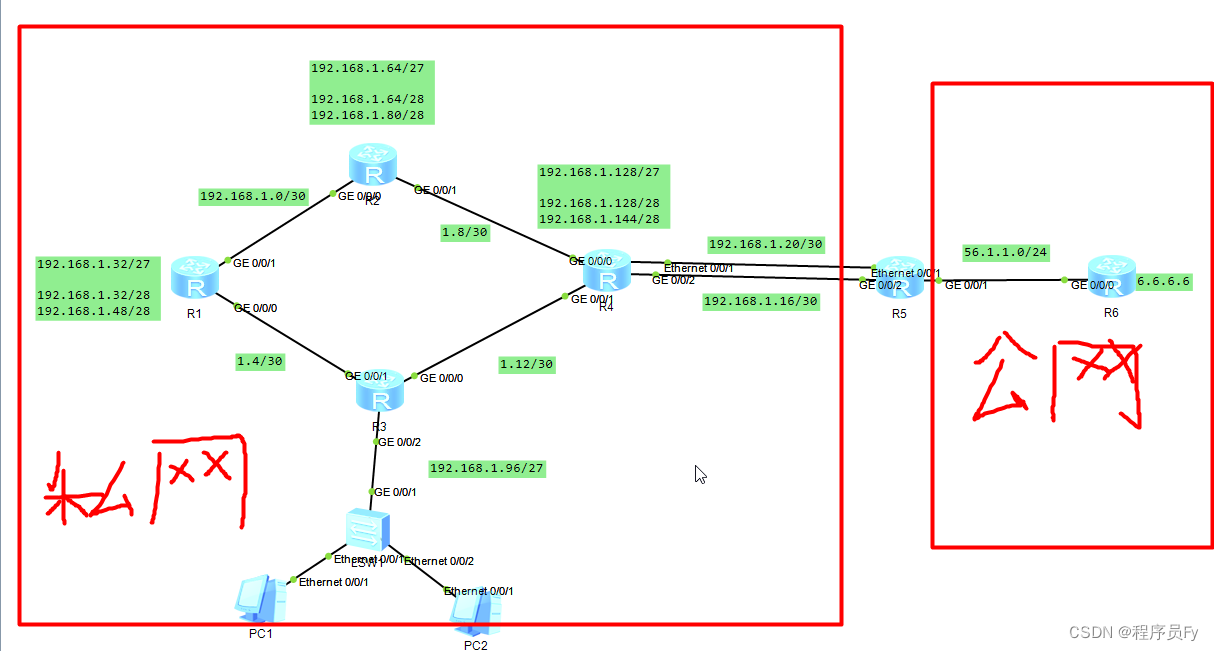
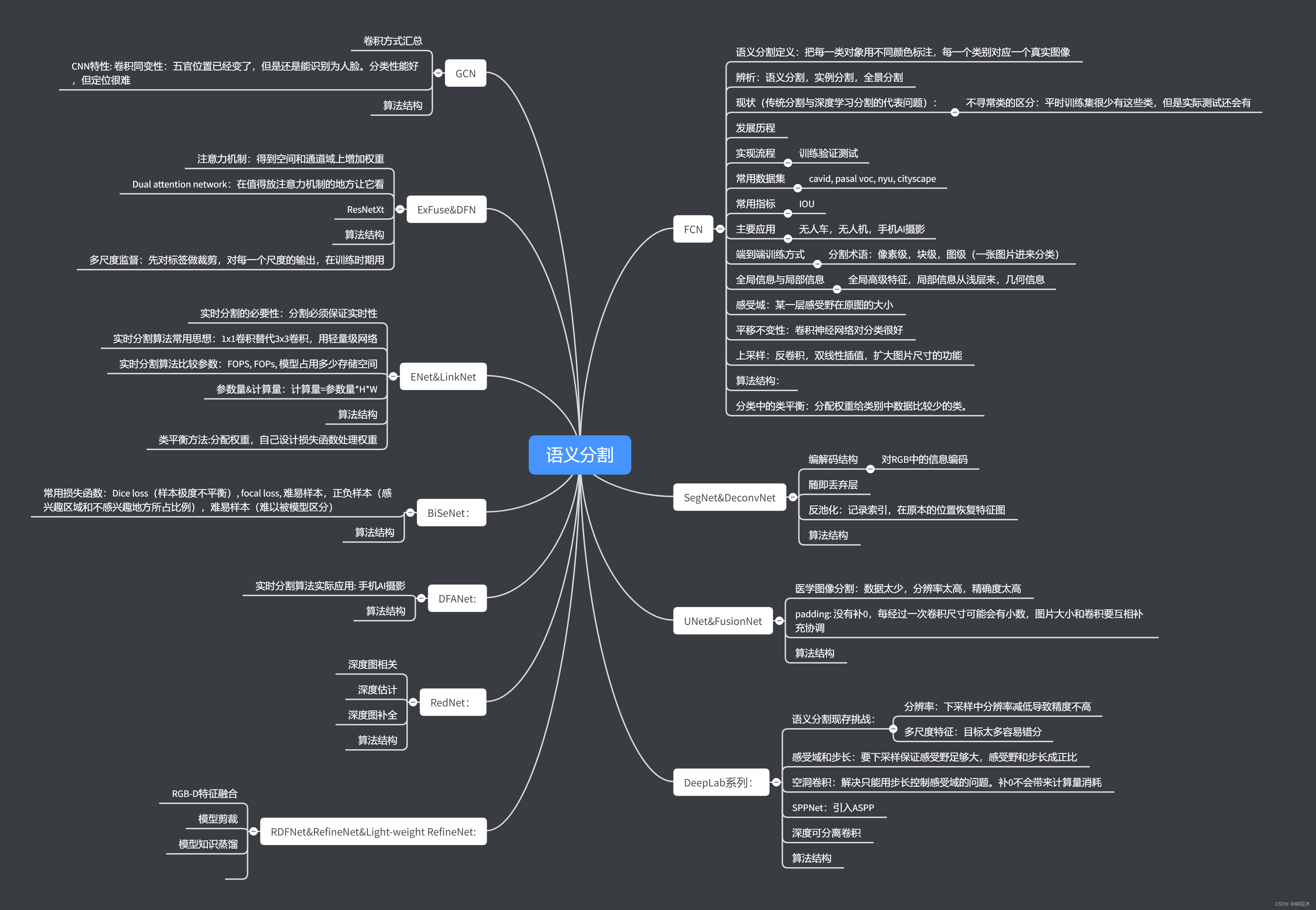
目录

1、隐性语义分析

2、奇异值分解

2.1 左奇异向量U

2.2 奇异值向量S

2.3 右奇异值向量V^T

2.4 SVD矩阵的方向

2.5 主题约简

---

1、隐性语义分析

        隐形语义分析基于最古老和最常用的降维技术–奇异值分解(SVD)。SVD将一个矩阵分解成3个方阵，其中一个是对角矩阵。SVD的一个应用是求逆矩阵。一个矩阵可以分解成3个更简单的方阵，然后对这些方阵求转置后再把它们相乘，就得到了原始矩阵的逆矩阵。

        利用SVD，LSA（Latent Semantic Analysis）可以将TF-IDF词频-文档矩阵分解成3个更简单的矩阵，揭示了原始TF-IDF矩阵的一些性质，可以利用这些性质来简化原始矩阵。可以在将这些矩阵相乘之前对它们进行截断处理（忽略一些行和列），这将减少在向量空间模型中需要处理的维数。这些截断的矩阵相乘并不能得到和原始TF-IDF矩阵完全一样的矩阵，然而它们却给出了一个更好的矩阵。文档的新表示方式包含了这些文档的本质，即隐性语义。

        隐性语义是一种数学上的技术，用于寻找对任意一组NLP向量进行最佳线性变换（旋转和拉伸）的方法，这些NLP向量包括TF-IDF向量和词袋向量。对许多应用来说，最好的变换方法是将坐标轴（维度）对齐到新向量中，使其在词频上具有最大的散度（spread）或方差（variance）。然后，我们可以在新的向量空间中去掉那些对不同文档的方差贡献不大的维度。

        LSA使用SVD查找导致数据中最大方差的词的组合。我们可以旋转TF-IDF向量，使旋转后的向量的新维度（基向量）与这些最大方差方向保持一致。“基向量”是新向量空间的坐标轴。每个维度（轴）都变成了词频的组合，而不是单个的词频，因此，可以把这些维度看作是构成语料库中各种“主题”词的加权组合。

        机器不能理解词的组合所表达的意义，只能理解这些词是在一起。当它看到像“dog”，“cat”，"love"这样的词总是出现在一起时，就会把它们放到一个主题中。机器并不知道这样的主题可能是关于“pets”的。这个主题可能包含很多词，包括“domesticated”和“feral”这种意义完全相反的词，如果它们经常一起出现在同一篇文档中，那么LSA会给它们赋予相同主题下的高分。

        LSA提供了另外一条有用的信息。类似于TF-IDF的IDF部分，LSA告诉我们向量中更多哪些维度对文档的语义（含义）很重要。于是，可以丢弃文档之间方差最小的维度（主题）。对于任何机器学习算法来说，这些小方差的主题通常是干扰因素和噪声。如果每篇文档都有大致相同含量的某个主题，而该主题却不能帮助我们区分这些文档，那么就可以删除这个主题。这将有助于泛化向量表示，因此当将LSA用于流水线上从没见过的新文档时，即使这篇文档来自完全不同的上下文，它也会工作得很好。

        LSA将更多的意义压缩到更少的维度中。我们只需要保留高方差维度，即语料库以各种方式（高方差）讨论的主要主题。留下来的每个维度都成为“主题”，包含所有捕捉到的词的某种加权组合。

2、奇异值分解

from nlpia.book.examples.ch04_catdog_lsa_sorted import lsa_models, prettify_tdm
bow_svd, tfidf_svd = lsa_models()
print(prettify_tdm(**bow_svd))

        上面是一个文档-词频矩阵，其中每一行都是文档对应的词袋向量。上述包含11（0~10）篇使用了词汇表中的6个词（cat, dog, apple, lion, nyc, love）的文档。遗憾的是，排序算法和大小有限的词汇表创建了几个完全相同的词袋向量（NYC,apple）。但是，SVD应该能够“看到”这一点，并将主题分配给这对词。

        下面将首先在词频-文档矩阵上使用SVD，代码为：

tdm = bow_svd['tdm']
print(tdm)

        无论是基于词袋的词项频-文档矩阵还是基于TF-IDF的词频-文档矩阵上运行SVD，SVD都会找到属于同类词的组合。SVD通过计算词频-文档矩阵的列（词项）之间的相关度来寻找那些同时出现的词。SVD能同时发现文档间词项使用的相关性和文档之间的相关性。利用这两条信息，SVD还可以计算出语料库中方差最大的词项的线性组合。这些词项频率的线性组合将成为主题。只保留那些在语料库中包含信息最多、方差最大的主题。SVD同时也提供了词频-文档向量的一个线性变换（旋转），它可以将每篇文档的向量转换为更短的主题向量。

        SVD将相关度高（因为它们经常一起出现在相同的文档中）的词项组合在一起，同时这一组合在一组文档中出现的差异很大。认为这些词的线性组合就是主题。这些主题会将词袋向量（或TF-IDF向量）转换为主题向量，这些主题向量会给出文档的主题。SVD（LSA的核心）用数学符号表示如下：

        m为词汇表中的词项数量，n为语料库中的文档数量，p为语料库中的主题数量。

2.1 左奇异向量U

        U矩阵包含词频-主题矩阵，它给出了词所具有的上下文信息。这是NLP中最重要的用于语义分析的矩阵。基于词在统一文档中的共现关系，U给出了词与主题之间的相互关联。在截断（删除列）之前，它是一个方阵，其行数和列数与词汇表中的词数（m）相同。

import numpy as np
import pandas as pd
U, s, Vt = np.linalg.svd(tdm)
print(pd.DataFrame(U, index=tdm.index).round(2))

        U矩阵包含所有的主题向量，其中每一列主题向量对应语料库中的每一个词。它可以用作一个转换因子，将词-文档向量（TF-IDF向量或词袋向量）转换为主题-文档向量。只需将U矩阵转置（主题-词项矩阵）乘以任何词项-文档列向量，就可以得到一个新的主题-文档向量，这是因为U矩阵中每个元素位置上的权重或得分，分别代表每个词对每个主题的重要程度。

2.2 奇异值向量S

        S矩阵是一个对角方阵，其对角线上的元素即为“奇异值”。奇异值给出了在新的语义（主题）向量空间中每个维度所代表的信息量。

print(s.round(1))
S = np.zeros((len(U), len(Vt)))
np.fill_diagonal(S, s)
print(pd.DataFrame(S).round(1))

 

        同U矩阵一样，6个词6个主题的语料库的S矩阵有6行（p），但是它有很多列是（n）都是0.每篇文档都需要一个列向量来表示，这样就可以将S乘以后面马上要用到的文档-文档矩阵V^T。因为目前还没有勇敢截断该对角矩阵来降维，所以词汇表中的词项数就是主题数。

        这里的维度（主题）是这样构造的：第一个维度包含关于语料库的最多信息（前面已经解释的方差）。这样，当想要截断主题模型时，可以一开始将右下角的维度归零，然后往左上角移动，当截断主题模型造成的错误开始对整个NLP流水线错误产生显著影响时，就可以停止将这些奇异值归零。

2.3 右奇异值向量V^T

        V^T是一个文档-文档矩阵，该矩阵将在文档之间提供共享语义，因为它度量了文档在新的文档语义模型中使用相同主题的频率。

print(pd.DataFrame(Vt).round(2))

        就像S矩阵，当把新的词频-文档向量转换成主题向量空间时，可以忽略VT矩阵。仅仅用VT矩阵来检查主题向量的准确性，以重建用于“训练”该矩阵的原始词项-文档向量。

2.4 SVD矩阵的方向

        机器学习训练集对应的样本-特征矩阵中的每一行都是一篇文档，而每一列都代表该文档的一个词或特性。但是要直接进行SVD线性代数运算时，矩阵需要转换成词频-文档格式。

        注意： 矩阵的命名和大小描述先由行开始，然后才是列。因此，词频-文档矩阵的行代表词，列代表文档。矩阵的维数（大小）描述也是如此。一个2*3矩阵有2行3列，这意味着np.shape()的结果为(2,3)，而len()的结果为2。在NLP训练集中，向量是行向量，而在传统的线性代数运算中，向量通常被认为是列向量。

        警告： 如果使用scikit-learn，必须将特征-文档矩阵转置，以创建一个文档-特征矩阵，然后将其传递到模型的.fit()和.predict()方法中。训练集矩阵中的每一行都应该是特定样本文本（通常是文档）的特征向量。

2.5 主题约简

        得到了一个主题模型，它可以将词频向量转换为主题权重向量。但是因为主题数和词数一样多，所以得到的向量空间模型的维数和原来的词袋向量一样多。到目前为止，还没有减少维数。

        这里可以忽略S矩阵，因为U矩阵的行和列已经排列妥当，以使最重要的主题（具有最大奇异值）都在左边。可以忽略S的另一个原因是，将在此模型中使用的大部分词-文档向量（如TF-IDF向量），都已经进行了归一化处理。最后，如果这样设置的话，它只会生成更好的主题模型。
因此，开始砍掉U右边的列。但是稍等一下，到底需要多少个主题才足以捕捉文档的本质呢？度量LSA精确率的一种方法是看看从主题-文档矩阵重构词项-文档矩阵的精确率如何。

err = []
for numdim in range(len(s), 0, -1):
    S[numdim - 1, numdim - 1] = 0
    reconstructed_tdm = U.dot(S).dot(Vt)
    err.append(np.sqrt(((reconstructed_tdm - tdm).values.flatten()**2).sum() / np.product(tdm.shape)))
print(np.array(err).round(2))

        Out[1]:[0.06 0.12 0.17 0.28 0.39 0.55]
        当使用奇异向量为11篇文档重构词频-文档矩阵时，截断的内容越多，误差就越大。如果大家使用前面的3个主题模型为每篇文档重构词袋向量，那么将有大约28%的均方根误差。随着主题模型丢弃的维度越来越多精确率不断下降。

        LSA背后的SVD算法会“注意”到某些词总在一起使用，并将它们放在一个主题中。这就是它可以“无偿”获得几个维度的原因。即使不打算在流水线中使用主题模型，LSA（SVD）也可以是为流水线压缩词频-文档矩阵以及识别潜在复合词或n-gram的一种好方法。