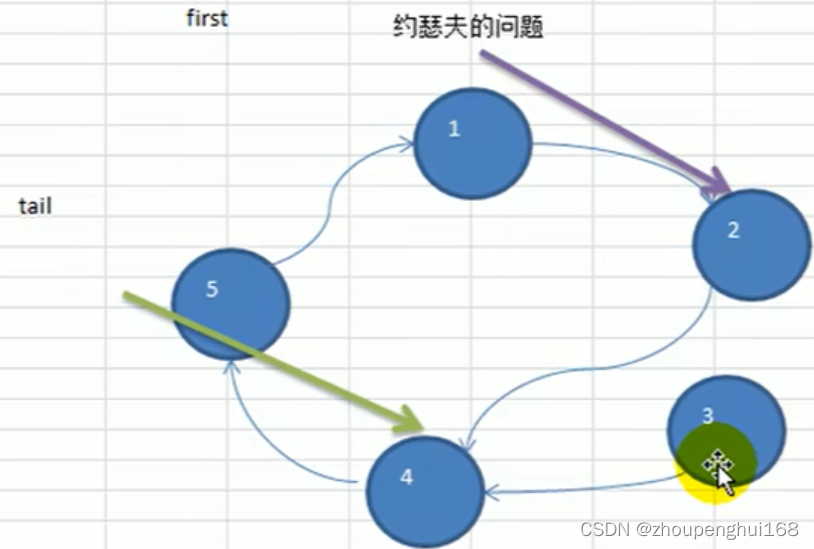
一.约瑟夫问题
josephu 问题:
设编号为1, 2 ,... n 的n个人围坐一圈, 约定编号为 k (1<=k<=n )的人从 1 开始报数,数到m的那个人出列,它的下一位又从1开始报数,数到 m 的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列
提示:
用一个不带头结点的循环链表来处理josephu问题,先构成一个有 n 个结点的单循环链表,然后由 k 结点起从1开始计数,计到 m 时,对应结点从链表中删除,然后再从被删除结点的下一个结点又从 1 开始计数,直到最后一个结点从链表中删除,算法结束

 代码如下:
代码如下:
package main
import (
"fmt"
)
//定义一个结构体
type Boy struct {
no int //编号
next *Boy // 指向下一个小孩的指针
}
//编写一个函数,构建一个单向环形链表
//num:表示要构建的小孩个数
//*Boy:返回环形链表的第一个小孩的指针
func AddBoy(num int) *Boy {
first := &Boy{} // 空指针
curBoy := &Boy{} // 空指针: 由逻辑分析得出,要构成一个循环单向链表,需要一个辅助指针
//判断num是否符合要求
if num < 1 {
fmt.Println("num不正确")
return first
}
//循环构建环形链表
for i := 1; i <= num; i++ {
boy := &Boy{
no: i,
}
//1.第一个小孩比较特殊
if i == 1 {
first = boy
curBoy = boy
curBoy.next = first // 形成一个环形链表
} else {
curBoy.next = boy
curBoy = boy
curBoy.next = first // 形成一个环形链表
}
}
return first
}
//显示单向环形链表
func ShowBoy(first *Boy) {
//处理环形链表为空的情况
if first.next == nil {
fmt.Println("链表为空")
return
}
//创建一个辅助指针,帮助遍历
curBoy := first
for {
fmt.Printf("小孩编号:%d\n", curBoy.no)
//退出条件: curBoy.next == first
if curBoy.next == first {
break
}
//下一个
curBoy = curBoy.next
}
}
//获取小孩总的个数
func GetNum(first *Boy) (num int) {
//处理环形链表为空的情况
if first.next == nil {
fmt.Println("链表为空")
return num
}
//创建一个辅助指针,帮助遍历
curBoy := first
for {
//退出条件: curBoy.next == first
if curBoy.next == first {
break
}
//下一个
curBoy = curBoy.next
num++
}
return num
}
/*
编号为1,2,...,n个小孩围坐在一圈,约定编号为k(1<=k<=n)的人从1开始报数,
数到m的那个人出列,它的下一位又从1开始报数,数到m的那个人又出列,依次类推,
直到所有人出列为止,由此产生一个出队编号的序列
*/
//分析:
//1.编写一个函数PlayGame(first *Boy, startNo int, countNum int)
//2.最后使用一个算法,按照要求,在环形链表中留下最后一个人
func PlayGame(first *Boy, startNo int, countNum int) {
//1.空的链表处理
if first.next == nil {
fmt.Println("空链表")
return
}
//2.判断startNo <= 小孩个数
num := GetNum(first)
if startNo > num {
fmt.Println("开始小孩个数不正确")
return
}
//定义一个辅助指针,帮助删除
tail := first
//3.让tail指向最后一个小孩,这个tail非常重要,因为在删除小孩的时候需要用到
for {
if tail.next == first { // 说明tail到了最后一个小孩了
break
}
tail = tail.next
}
//3.让first移动到startNo(后面删除时,就以first为准)
for i := 1; i <= startNo - 1; i++ {
first = first.next
tail = tail.next
}
//5.开始数countNum,然后删除first指向的小孩
for {
//开始数countNum -1 次
for i := 1; i <= countNum - 1; i++ {
first = first.next
tail = tail.next
}
fmt.Printf("小孩编号为%d 出圈 -> \n", first.no)
//删除first执行的小孩
first = first.next
tail.next = first
//判断 如果 tail == first 说明只有一个小孩了
if tail == first {
break
}
}
fmt.Printf("小孩编号为%d 最后出圈 -> \n", first.no)
}
func main() {
first := AddBoy(5)
ShowBoy(first)
PlayGame(first, 2, 3)
}二.排序
1.排序的基本介绍
排序是将一组数据,依照指定的顺序进行排列的过程,常见的排序有:
(1).冒泡排序
(2).选择排序
(3).插入排序
(4).快速排序
2.冒泡排序
见[go学习笔记.第八章.排序和查找] 1.排序,查找的基本介绍
3.选择排序
基本介绍
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,经过和其他元素重整,再依原则交换位置后达到排序的目的
选择排序思想
选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从 R[0]~R [ n - 1] 中选取最小值,与 R[0]交换,第二次从 R[1]~R[n - 1]中选取最小值,与 R[1]交换,第三次从 R[2]~R[n - 1]中选取最小值,与 R[2]交换, … ,第 i 次从 R[i - 1] ~ R [ n - 1]中选取最小值,与 R[i - 1]交换, … 第 n - 1 次从 R[n - 2]~ R[n ~ 1中选取最小值,与 R [ n - 2 ]交换,总共通过 n - 1 次,得到一个按排序码从小到大排列的有序序列

代码如下:
package main
import(
"fmt"
)
//编写一个函数SelectSort(arr *[5]int) 完成排序
func SelectSort(arr *[5]int) {
for j := 0; j < len(arr) - 1; j++ {
//1.假设arr[0]为最大值
max := arr[j] //最大值
maxIndex := j //最大值的下标
//2.遍历后面的1~len(arr) - 1
for i := j + 1; i < len(arr); i++ {
if max < arr[i] { //找到真正的最大值
max = arr[i]
maxIndex = i
}
}
//交换
if maxIndex != j {
arr[j], arr[maxIndex] = arr[maxIndex], arr[j]
}
fmt.Printf("第%d次交换后,arr = %v\n", j + 1, *arr)
}
}
func main() {
arr := [5]int{80, 12, 43, 24, 89}
SelectSort(&arr)
fmt.Println(arr)
}4.插入排序
基本介绍:
插入式排序属于内部排序法,是对干欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的
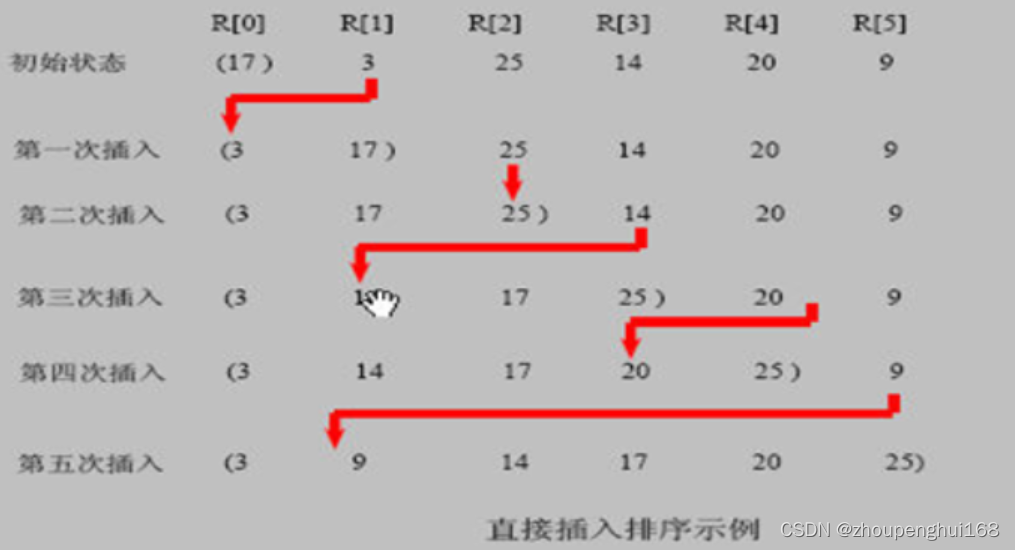
插入排序法思想:
插入排序(Insertion Sorting)的基本思想是:把 n 个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有 n - 1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表

package main
import(
"fmt"
)
//编写一个方法,实现插入排序
func insertSort(arr *[5]int) {
for i := 1; i < len(arr); i++ { //定义要比较的次数
//给第i个元素找到合适的位置
insertVal := arr[i]
insertIndex := i - 1 // 要比较元素的下标: 始终是当前元素下标的前一个元素下标
//从大到小
for insertIndex >= 0 && arr[insertIndex] < insertVal {
//数据后移
arr[insertIndex + 1] = arr[insertIndex]
insertIndex-- //要比较的下标前移
}
//比较完后插入
if insertIndex + 1 != i {
arr[insertIndex + 1] = insertVal
}
fmt.Printf("第%d次插入后数据:%v\n", i, *arr)
}
}
func main() {
arr := [5]int{11,79,45,7,90}
fmt.Println(arr)
insertSort(&arr)
fmt.Println(arr)
}5.快速排序
基本介绍
快速排序(Quicksort)是对冒泡排序的一种改进,基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
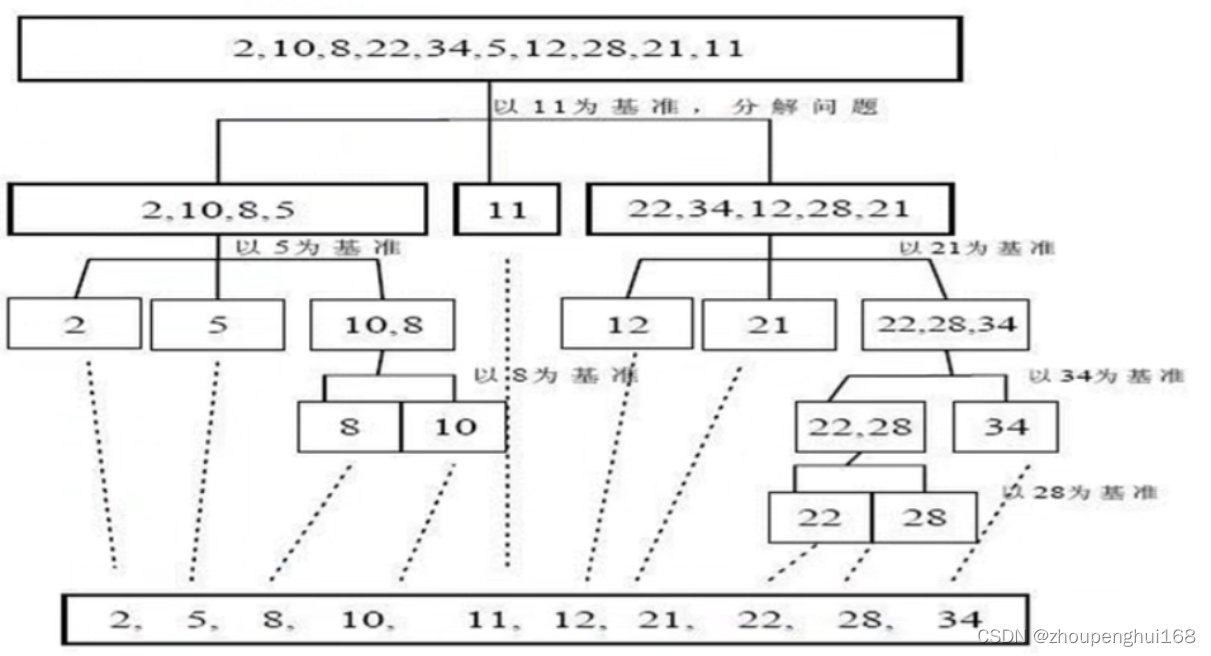
案例要求:
对[-9 , 78 , 0 , 23 ,-567 , 70]进行从小到大的排序,要求使用快速排序
说明:
(1).如果取消左右递归,结果是 -9 -567 0 23 78 70
(2).如果取消右递归,结果是 -567 -9 0 23 78 70
(3).如果取消左递归,结果是 -9 -567 0 23 70 78
package main
import(
"fmt"
)
//left: 表示数组左边的下标
//right: 表示数组右边的下标
//array: 表示要排序的数组
func QuickSort(left int, right int, array *[6]int) {
l := left
r := right
//pivot 是中轴,支点
pivot := array[(left + right) / 2]
//for循环目的是将比pivot小的数放到左边,比pivot大的数放到右边
for ;l < r; {
//从pivot的左边找到大于等于pivot的值
for ; array[l] < pivot; {
l++
}
//从pivot的右边找到小于等于pivot的值
for ; array[r] > pivot; {
r--
}
//说明找到了: 本次分解任务完成
if l >= r {
break
}
//交换
array[l], array[r] = array[r], array[l]
//优化
if array[l] == pivot {
l++
}
if array[r] == pivot {
r--
}
}
//如果l == r, 则再移动一下
if l == r {
l++
r--
}
//向左递归
if left < r {
QuickSort(left, r, array)
}
//向右递归
if right > l {
QuickSort(l, right, array)
}
}
func main() {
arr := [6]int{-8, 66, 0, 12, -37, 80}
fmt.Println(arr)
QuickSort(0, len(arr) - 1, &arr)
fmt.Println(arr)
}三.栈
1.看一个需求
请输入一个表达式计算式: [7 * 2 * 2 - 5 +1 - 5 + 3 - 3 ]点击计算
请问:计算机底层是如何运算得到结果的?注意不是简单的把算式列出运算,因为看这个算式 7 * 2 * 2 - 5 ,但是计算机怎么理解这个算式的 (对计算机而言,它接收到的就是一个字符串 )
2.栈的介绍
有些程序员也把栈称为堆栈:即栈和堆栈是同一个概念
(1).栈的英文为( stack)
(2).栈是一个先入后出(FILO-First In Last Out)的有序列表
(3).栈(stack)是限制线性表中元素的插入和删除,只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)
(4).根据堆栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
3.栈的入栈和出栈示意图
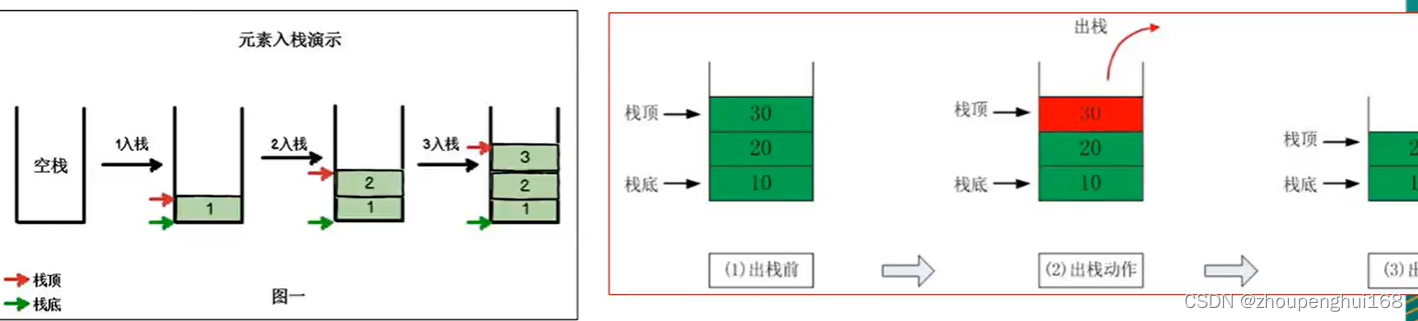
4.栈的应用场景
(1).子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中
(2).处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中
(3).表达式的转换与求值
(4).二叉树的遍历
(5).图形的深度优先(depth-first)搜索法
5.栈的案例
用数组模拟栈的使用,由于堆栈是一种有序列表,当然可以使用数组的结构来储存栈的数据内容,数组模拟栈的出栈,入栈等操作
package main
import(
"fmt"
"errors"
)
//使用数组模拟一个栈的作用
type Stack struct {
MaxTop int //栈最大可以存放数个数
Top int //表示栈顶,因为栈顶固定,因此直接使用Top
arr [5]int //数组模拟栈
}
func (this *Stack) Push(val int) (err error) {
//先判断栈是否满了
if this.Top == this.MaxTop - 1 {
fmt.Println("栈满了")
return errors.New("栈满了")
}
this.Top++
//放入数据
this.arr[this.Top] = val
return
}
func (this *Stack) Pop() (val int, err error) {
//先判断栈是否为空
if this.Top == - 1 {
fmt.Println("栈空了")
return 0, errors.New("栈空了")
}
//先取值,再top--
val = this.arr[this.Top]
this.Top--
return val, nil
}
//遍历栈,注意需要从栈顶开始遍历
func (this *Stack) List() {
//先判断栈是否满了
if this.Top == - 1 {
fmt.Println("栈空了")
return
}
for i := this.Top; i >= 0; i-- {
fmt.Printf("arr[%d] = %d\n", i, this.arr[i])
}
}
func main() {
//初始化一个栈
stack := &Stack {
MaxTop: 5, //表示最多存放5个数到栈中
Top: -1, //当栈顶为-1,表示栈为空
}
//入栈
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(4)
stack.Push(5)
//遍历
stack.List()
//出栈
val, _ := stack.Pop()
fmt.Printf("出栈:%d\n", val)
stack.List()
//出栈
val, _ = stack.Pop()
fmt.Printf("出栈:%d\n", val)
stack.List()
//出栈
val, _ = stack.Pop()
fmt.Printf("出栈:%d\n", val)
stack.List()
//出栈
val, _ = stack.Pop()
fmt.Printf("出栈:%d\n", val)
stack.List()
//出栈
val, _ = stack.Pop()
fmt.Printf("出栈:%d\n", val)
stack.List()
//出栈
val, _ = stack.Pop()
if val == 0 {
fmt.Println("栈空了")
}
}6.栈实现综合计算器

package main
import(
"fmt"
"errors"
"strconv"
)
//使用数组模拟一个栈的作用
type Stack struct {
MaxTop int //栈最大可以存放数个数
Top int //表示栈顶,因为栈顶固定,因此直接使用Top
arr [20]int //数组模拟栈
}
func (this *Stack) Push(val int) (err error) {
//先判断栈是否满了
if this.Top == this.MaxTop - 1 {
fmt.Println("栈满了")
return errors.New("栈满了")
}
this.Top++
//放入数据
this.arr[this.Top] = val
return
}
func (this *Stack) Pop() (val int, err error) {
//先判断栈是否为空
if this.Top == - 1 {
fmt.Println("栈空了")
return 0, errors.New("栈空了")
}
//先取值,再top--
val = this.arr[this.Top]
this.Top--
return val, nil
}
//遍历栈,注意需要从栈顶开始遍历
func (this *Stack) List() {
//先判断栈是否满了
if this.Top == - 1 {
fmt.Println("栈空了")
return
}
for i := this.Top; i >= 0; i-- {
fmt.Printf("arr[%d] = %d\n", i, this.arr[i])
}
}
//判断一个字符是不是一个运算符(+,-,*,/),利用ASCII
func (this *Stack) IsOper(val int) bool {
if val == 42 || val == 43 || val == 45 || val == 47 {
return true
} else {
return false
}
}
//运算的方法
func (this *Stack) Cal(num1 int, num2 int, oper int) int {
res := 0
switch oper {
case 42:
res = num2 * num1
case 43:
res = num2 + num1
case 45:
res = num2 - num1
case 47:
res = num2 / num1
default:
fmt.Println("运算符错误")
}
return res
}
//编写方法,返回某个运算符的优先级[程序员规定]
//*,/ ==> 1, +,- ==> 0
func (this *Stack) Priority(oper int) int {
res := 0
if oper == 42 || oper == 47 {
res = 1
} else if oper == 43 || oper == 45 {
res = 0
}
return res
}
func main() {
//初始化栈
//数栈
numStack := &Stack {
MaxTop: 20, //表示最多存放5个数到栈中
Top: -1, //当栈顶为-1,表示栈为空
}
//符号栈
operStack := &Stack {
MaxTop: 20, //表示最多存放5个数到栈中
Top: -1, //当栈顶为-1,表示栈为空
}
exp := "30+20*6-21"
//定义一个index,帮助扫描
index := 0
//为了配合运算,定义需要的变量
num1 := 0
num2 := 0
oper := 0
result := 0
keepNum := "" // 处理多位数问题: 目的是用来做拼接的
for {
ch := exp[index:index+1] // 字符串
temp := int([]byte(ch)[0]) // 这个就是字符串对应的ASCII值
if operStack.IsOper(temp) { // 说明是符号
//如果operStack是一个空栈,直接入栈
if operStack.Top == -1 {
operStack.Push(temp)
} else {
//如果发现operStack栈顶的运算符的优先级大于等于当前准备入栈的运算符的优先级,
//就从符号栈Pop出,并从数栈也Pop两个数,进行运算,运算后的结果再重新入栈到数栈,
//符号再入符号栈
if operStack.Priority(operStack.arr[operStack.Top]) >=
operStack.Priority(temp) {
num1, _ = numStack.Pop()
num2, _ = numStack.Pop()
oper, _ = operStack.Pop()
result = operStack.Cal(num1, num2, oper)
//将计算的结果重新入栈
numStack.Push(result)
//将当前的符号压入符号栈
operStack.Push(temp)
} else {
operStack.Push(temp)
}
}
} else { // 说明是数字
//处理多位数问题,思路:
//1.定义一个变量keepNum string, 做拼接
keepNum += ch
//2.每次要向index的后面字符测试一下,看看是不是运算符,然后处理
//如果已经到表达式的最后了,则直接把keepNum Push
if index == len(exp) - 1 {
val, _ := strconv.ParseInt(keepNum, 10, 64)
numStack.Push(int(val))
} else {
// 向index后面测试看看是不是运算符
if operStack.IsOper(int([]byte(exp[index + 1: index + 2])[0])) {
val, _ := strconv.ParseInt(keepNum, 10, 64)
numStack.Push(int(val))
keepNum = ""
}
}
}
//继续扫描
//先判断index是否扫描到计算表达式的最后
if index + 1 == len(exp) {
break
} else {
index++
}
}
//如果扫描表达式完毕,依次从符号栈取出符号,然后从数栈取出两个数,
//运算后的结果,入数栈,直到符号栈为空
for {
if operStack.Top == -1 { //退出条件
break
}
num1, _ = numStack.Pop()
num2, _ = numStack.Pop()
oper, _ = operStack.Pop()
result = operStack.Cal(num1, num2, oper)
//将计算的结果重新入栈
numStack.Push(result)
}
//如果以上逻辑没有问题,那么结果就是数栈的最后一个数
res, _ := numStack.Pop()
fmt.Printf("表达式%s = %v\n", exp, res)
}四.递归
1.递归的一个应用场景
迷宫回溯问题
2.递归的概念
递归就是函数/方法自己调用自己,每次调用时传入不同的变量,递归有助于编程者解决复杂的问题,同时可以让代码变得简洁
3.快速入门
(1).打印问题
(2).阶乘问题
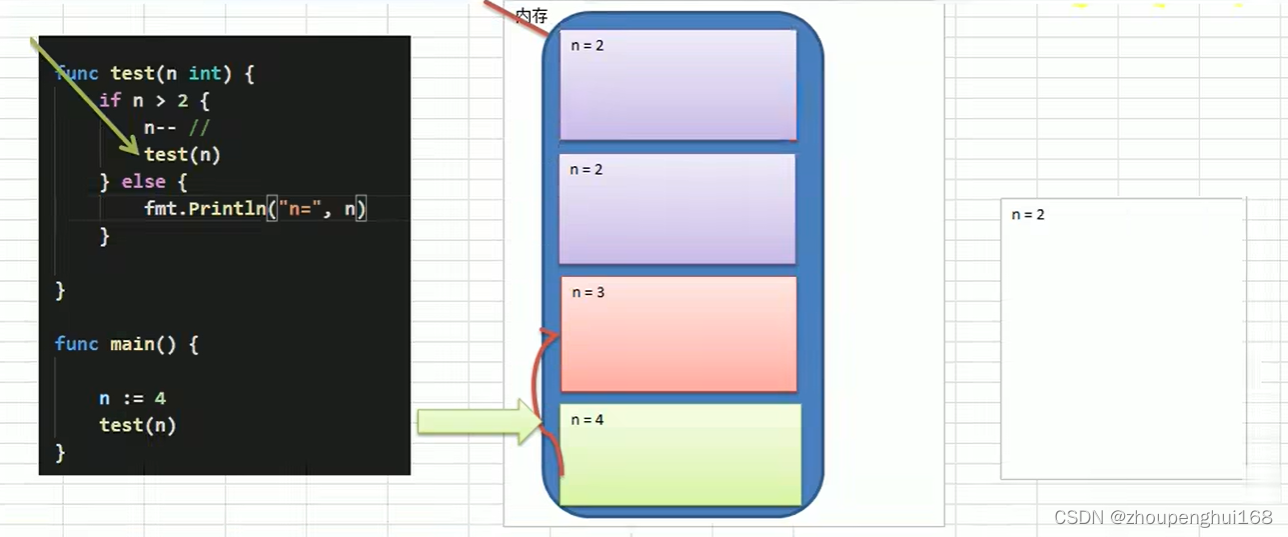
4.递归用于解决什么问题
(1).各种数学问题,如:皇后问题,汉诺塔,阶乘问题,迷宫问题,球和蓝子问题
(2).将用栈解决的问题
5.递归需要遵守的重要原则
(1).执行一个函数时,就创建一个新的受保护的独立空间(新函数栈
(2).函数的局部变量是独立的,不会相互影响,如果希望各个函数栈使用同一个数据,使用引用传递
(3).递归必须向退出递归的条件逼近 【 程序员自己必须分析 】 ,否则就是无限递归
(4).当一个函数执行完毕,或者遇到return ,就会返回,遵守谁调用,就将结果返回给谁,同时当函数执行完毕或者返回时,该函数本身也会被系统销毁
6.案例展示
package main
import(
"fmt"
)
//编写一个函数,完成找路
//myMap *[8][7]int:地图, 保证是同一个地图,故使用引用
//i, j :表示对地图的哪个点进行测试
func Setway(myMap *[8][7]int, i int, j int) bool {
//分析出什么情况下找到出路
//myMap[6][5]
if myMap[6][5] == 2 { //说明找到出路了
return true
} else { //说明要继续找
if myMap[i][j] == 0 { //如果这个点是可以探测的
//假设这个点是可以通的, 但是需要探测, 探测策略:上下左右
myMap[i][j] = 2
// if Setway(myMap, i - 1, j) { //上
// return true
// } else if Setway(myMap, i + 1, j) { // 下
// return true
// }else if Setway(myMap, i, j - 1) { //左
// return true
// }else if Setway(myMap, i, j + 1) { //右
// return true
// } else {
// myMap[i][j] = 3
// return false
// }
// 探测策略:下右上左
if Setway(myMap, i + 1, j) { //下
return true
} else if Setway(myMap, i, j + 1) { //右
return true
}else if Setway(myMap, i - 1, j) { //上
return true
}else if Setway(myMap, i, j - 1) { //左
return true
} else {
myMap[i][j] = 3
return false
}
} else { //说明这个点不能探测, 为1,是墙
return false
}
}
}
func main() {
//先创建一个二维数组,模拟迷宫
//规则:
//1.如果元素的值为1,表示一堵墙
//2.如果元素的值为0,表示没有走过的点
//3.如果元素的值为2,表示一个通路
//3.如果元素的值为3,表示走过的点,但是走不通
var myMap [8][7]int
//设置墙
//先把地图的最上和最下设置为1
for i := 0; i < 7; i++ {
myMap[0][i] = 1
myMap[7][i] = 1
}//先把地图的最左和最右设置为1
for i := 0; i < 8; i++ {
myMap[i][0] = 1
myMap[i][6] = 1
}
//加墙
myMap[3][1] = 1
myMap[3][2] = 1
//输出地图
for i := 0; i < 8; i++ {
for j := 0; j < 7; j++ {
fmt.Print(myMap[i][j], " ")
}
fmt.Println()
}
//探测
Setway(&myMap, 1, 1)
fmt.Println("探测完毕后的地图:")
for i := 0; i < 8; i++ {
for j := 0; j < 7; j++ {
fmt.Print(myMap[i][j], " ")
}
fmt.Println()
}
}五.哈希表(散列)
1.实际需求
有一个公司,当有新的员工来报道时,要求将该员工的信息加入(id,性别,年龄,住址,...),当输入该员工的id时,要求查找到该员工的所有信息
要求:
不使用数据库,尽量节省内存,速度越快越好=>哈希表(散列)
2.基本介绍
散列表( Hash table ,也叫哈希表),是根据关键码值(key value)而直接进行访问的数据结构,也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度,这个映射函数叫做散列函数,存放记录的数组叫做散列表
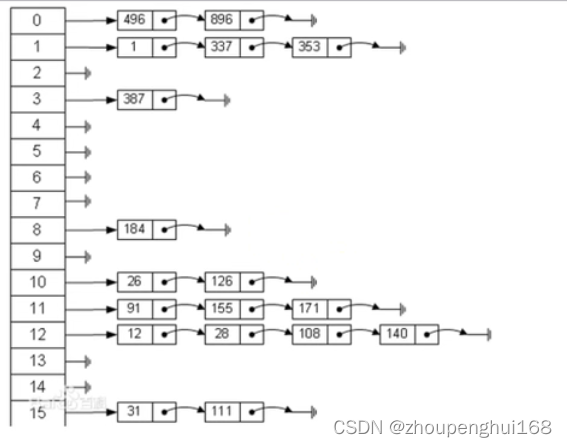
3.使用hash table来实现一个雇员的管理系统[增删改查]
应用实例google公司的一个上机题
有一个公司,当有新的员工来报道时,要求将该员工的信息加入( id ,性别,年龄,住址,...),当输入该员工的 id 时,要求查找到该员工的所有信息
要求:
(1).不使用数据库,尽量节省内存速度越快越好=>哈希表(散列)
(2).添加时,保证按照雇员的 id 从低到高插入
思路分析:
(1).使用链表来实现哈希表,该链表不带表头, 即:链表的第一个结点就存放雇员信息
(2).思路分析并画出示意图
(3).代码实现[增删改查],显示所有员工,按照id查询
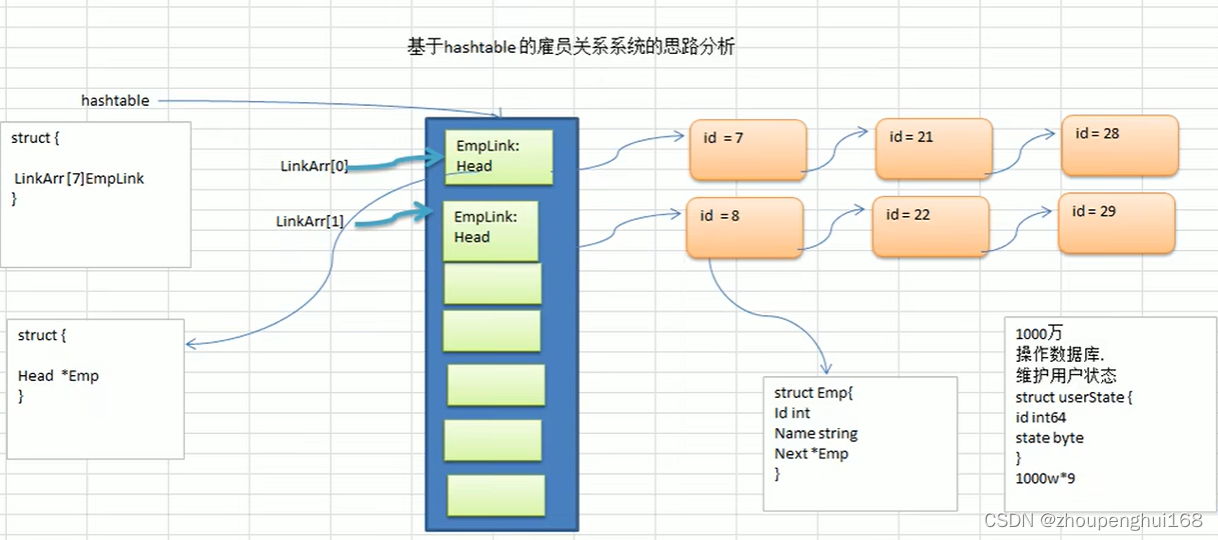
package main
import(
"fmt"
"os"
)
//定义emp
type Emp struct {
Id int
Name string
Next *Emp
}
//方法
func (this *Emp) ShowMe() {
fmt.Printf("链表%d对应的雇员编号%d信息为:id=%d,姓名:%v\n", this.Id % 7, this.Id, this.Id, this.Name)
}
//定义EmpLink
//EmpLink 不带表头,即第一个结点就存放雇员
type EmpLink struct {
Head *Emp
}
//显示链表的数据信息
func (this *EmpLink) ShowLink(no int) {
cur := this.Head // 辅助结点
if cur == nil {
fmt.Printf("链表%d没有雇员\n", no)
return
}
//遍历当前链表
fmt.Printf("链表%d对应的雇员信息\n", no)
for {
if cur != nil {
fmt.Printf("雇员信息:id=%d,姓名=%v => ", cur.Id, cur.Name)
cur = cur.Next
} else {
break
}
}
fmt.Println()
}
//添加雇员的方法
//要保证添加时,编号从小到大
func (this *EmpLink) Insert(emp *Emp) {
cur := this.Head //辅助指针
var pre *Emp = nil //辅助指针, 在cur前面
//如果当前的EmpLink是一个空链表
if cur == nil {
this.Head = emp
return
}
//如果不是一个空链表,给emp找到对应的位置并插入
//思路: 让cur和emp比较,然后让pre保持在cur前面
for {
if cur != nil {
//比较
if cur.Id >= emp.Id {
//找到位置
break
}
pre = cur
cur = cur.Next
} else {
break
}
}
//退出时,是否将emp加入到链表最后还是插入
pre.Next = emp
emp.Next = cur
}
//根据雇员id查找雇员
func (this *EmpLink) FindById(id int) *Emp {
cur := this.Head
for {
if cur != nil && cur.Id == id { // 找到了
return cur
} else if cur == nil {
break
}
cur = cur.Next
}
return nil
}
//定义HasTable,含有一个链表数组
type HashTable struct {
LinkArr [7]EmpLink
}
//给HaseTable编写一个ShowAll显示雇员的方法
func (this *HashTable) ShowAll() {
for i := 0; i < len(this.LinkArr); i++ {
this.LinkArr[i].ShowLink(i)
}
}
//给HaseTable编写一个Insert雇员的方法
func (this *HashTable) Insert(emp *Emp) {
//使用散列函数,确定将该雇员添加到哪条链表
linkNo := this.HashFun(emp.Id)
//使用对应的链表添加
this.LinkArr[linkNo].Insert(emp)
}
//给HaseTable编写一个Find雇员的方法
func (this *HashTable) FindById(id int) *Emp {
//使用散列函数,确定将该雇员属于哪条链表
linkNo := this.HashFun(id)
//使用对应的链表添加
return this.LinkArr[linkNo].FindById(id)
}
//编写一个散列方法
func (this *HashTable) HashFun(id int) int {
return id % 7 //得到一个值,就是对应的链表的下标
}
func main() {
key := ""
id := 0
name := ""
var hashtable HashTable
for {
fmt.Println("==============雇员菜单=============")
fmt.Println("==============input 表示添加雇员==============")
fmt.Println("==============show 表示展示雇员==============")
fmt.Println("==============find 表示查找雇员==============")
fmt.Println("==============exit 表示退出==============")
fmt.Println("请输入你的选择:")
fmt.Scanln(&key)
switch key {
case "input":
fmt.Println("请输入雇员id:")
fmt.Scanln(&id)
fmt.Println("请输入雇员名字:")
fmt.Scanln(&name)
emp := &Emp{
Id: id,
Name: name,
}
hashtable.Insert(emp)
case "show":
hashtable.ShowAll()
case "find":
fmt.Println("请输入雇员id:")
fmt.Scanln(&id)
emp := hashtable.FindById(id)
if emp != nil {
//编写一个方法,显示雇员信息
emp.ShowMe()
} else {
fmt.Println("没找到雇员")
}
case "exit":
os.Exit(0)
default:
fmt.Println("输入有误")
}
}
}六.二叉树的三种遍历方式
package main
import(
"fmt"
)
type Hero struct {
No int
Name string
Left *Hero
Right *Hero
}
//前序遍历: 先输出root根节点,然后输出左子树,然后输出右子树
func PreOrder(node *Hero) {
if node != nil {
fmt.Printf("no=%d,name=%v\n", node.No, node.Name)
PreOrder(node.Left)
PreOrder(node.Right)
}
}
//中序遍历: 先输出root的左子树,然后输出右子树,然后输出root根节点
func InfixOrder(node *Hero) {
if node != nil {
InfixOrder(node.Left)
fmt.Printf("no=%d,name=%v\n", node.No, node.Name)
InfixOrder(node.Right)
}
}
//后序遍历: 先输出root的右子树,然后输出root根节点,然后输出左子树
func PostOrder(node *Hero) {
if node != nil {
InfixOrder(node.Left)
InfixOrder(node.Right)
fmt.Printf("no=%d,name=%v\n", node.No, node.Name)
}
}
func main(){
//构建二叉树
root := &Hero {
No: 1,
Name: "及时雨",
}
left1 := &Hero {
No: 2,
Name: "智多星",
}
right1 := &Hero {
No: 3,
Name: "玉麒麟",
}
root.Left = left1
root.Right = right1
right2 := &Hero {
No: 4,
Name: "豹子头",
}
right1.Right = right2
PreOrder(root)
InfixOrder(root)
}[上一节][go学习笔记.第十八章.数据结构] 1.基本介绍,稀疏数组,队列(数组实现),链表