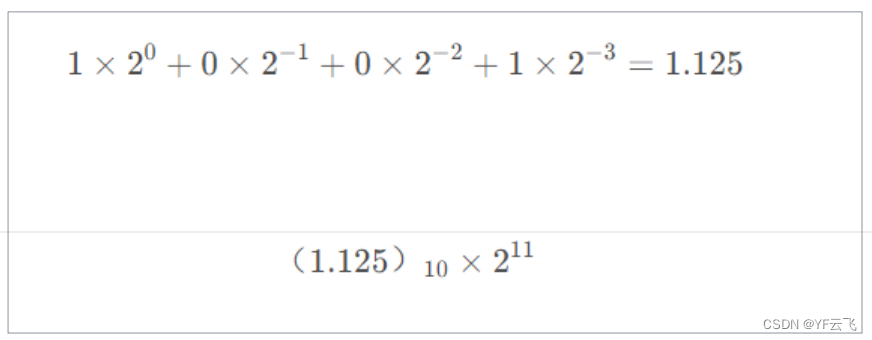计算机组成原理“上分秘籍”——数据的表示和运算

news2025/1/7 6:25:27

前言

上分地图

前言

上分地图

猜你想问

Q1：为何要研究数据表示问题？

Q2：什么叫数据表示？计算机中又有哪些方法？

正文

上分突破口1：进位计数法

例：二进制转为十进制

例：二进制转换为八进制和十六进制

各种进制的常见书写方式

⭐十进制数转换为任意进制数

上分突破口2：BCD码

上分突破口3：定点数的表示形式

定点小数

定点整数

原码

反码

补码

上分突破口4：IEEE754浮点数

两种格式：

猜你想问

Q1：为何要研究数据表示问题？

数据表示是计算机硬件与软件之间的接口，了解计算机中数据表示是了解各主要部件工作原理的重要前提。

Q2：什么叫数据表示？计算机中又有哪些方法？

数据表示指能由计算机硬件直接识别出来的数据类型，既可以用计算机硬件直接表示出来，并能由计算机指令直接调用该数据类型。

计算机中常用的数值数据表示方法有：定点数、浮点数。

接下来，速速与笔者一起双排上分吧！

正文

在计算机系统内部 , 所有的信息 都是用 二进制进行编码的。

上分突破口1：进位计数法

常用的进位计数法有十进制、二进制、八进制、十六进制等。

基数: 每个数码位所用到的不同符号的个数, r进制的基数为r。

十进制的基数为10(0~9),每个数位记满10就向高位进位, 即"逢十进一"。

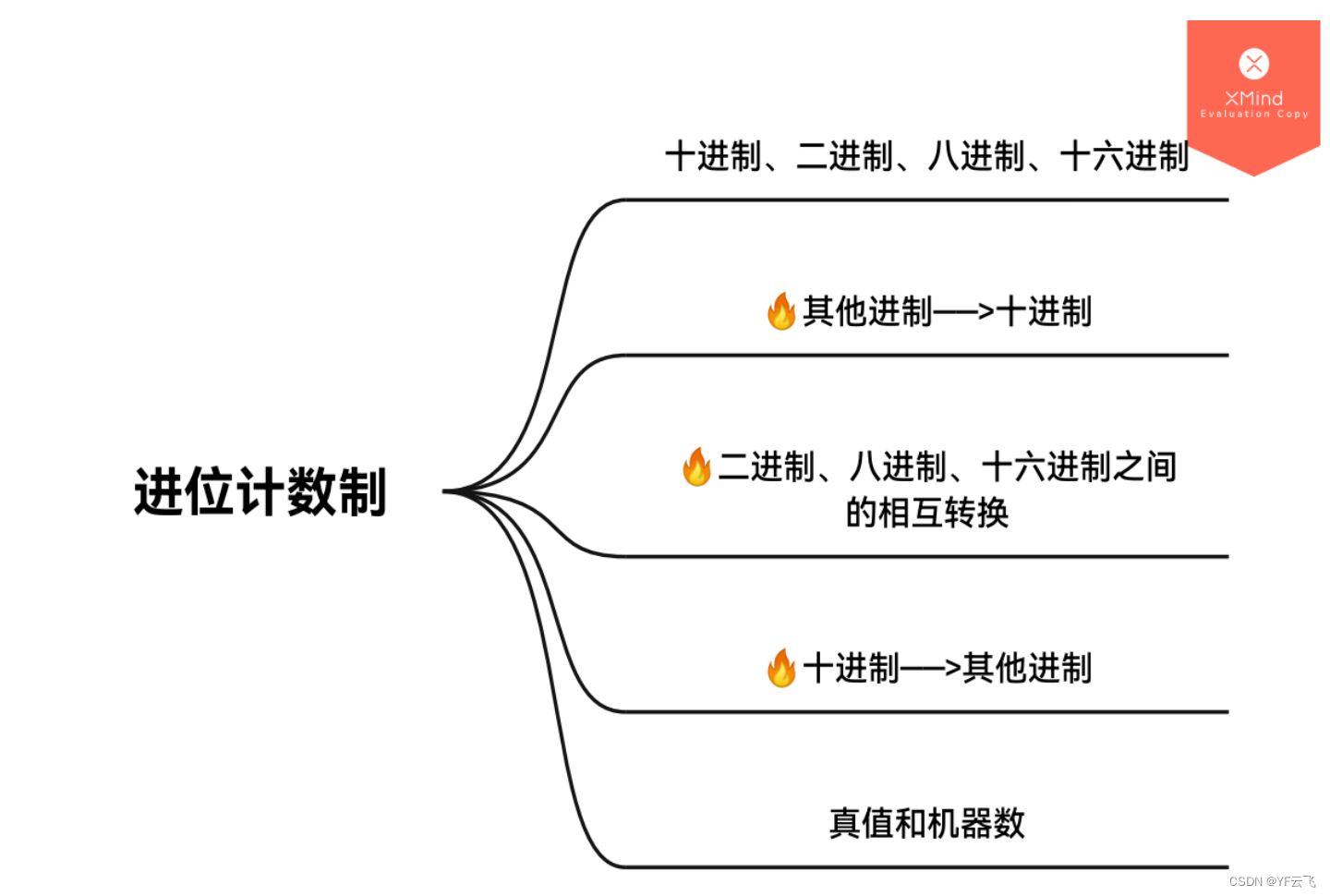
二进制： 0, 1

八进制： 0, 1, 2, 3, 4, 5, 6, 7

十进制： 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

十六进制： 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

例：二进制转为十进制

将二进制数转换成对应的十进制数的方法是“按权展开求和”。

例：二进制转换为八进制和十六进制

对于一个二进制混合数 ( 即包含整数部分 , 又包含小数部分 ), 在转换时应以小数点为界。

其整数部分 , 从小数点开始往左数 , 在数的最左边可根据需要加 "0 补齐 ";

对于小数部分 , 从小数点开始往右数 , 在数的最右边可根据需要加 "0" 补齐。

最终使总的位数为 3 或 4 的整数倍 , 然后分别用对应的八进制数或十六进制数取代。

二进制 👉 八进制

1111000101.01101

3 位一组 , 每组转换成对应的八进制符号

001 111 000 101 . 011 010

1 7 0 5 . 3 2 八进制（ 1705 . 32 ） 8

二进制 👉十六进制

1111000010.011010

4 位一组 , 每组转换成对应的十六进制符号

0011 1100 0010 . 0110 1000

3 C 2 . 6 8 十六进制（ 3C2 . 68 ) 16

各种进制的常见书写方式

二进制（ 1010001010010)2 1010001010010B

八进制 (1652)8

十六进制 (1652)16 1652H 0x1652

十进制 (1652)10 1652D

⭐十进制数转换为任意进制数

两种对应方法：

1、除基取余法(整数部分的转换): 整数部分除基取余, 最先取得的余数为数的最低位, 最后取得的余数为数的。

最高位, 商为0时结束。

2、乘基取整法(小数部分的转换): 小数部分乘基取整, 最先取得的整数为数的最高位, 最后取得的整数为数的。

最高位, 乘积为1.0时(或者满足精确位数)结束。

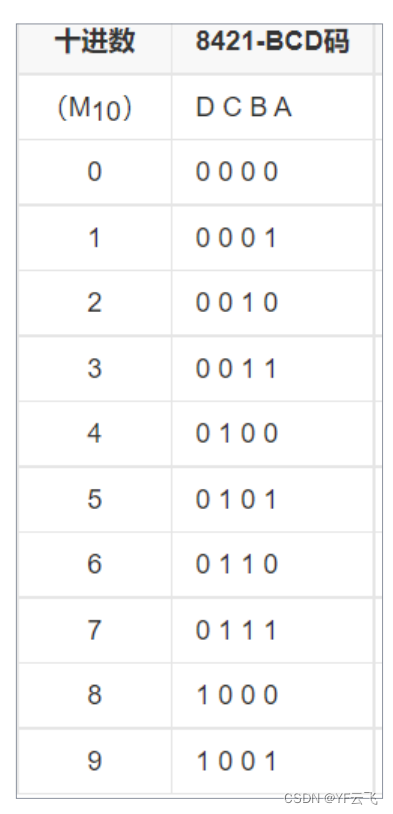
上分突破口2：BCD码

十进制数转换成二进制数 就要用到一种转换码， BCD 码就是其中的一种 , 每位 BCD 码用 四个二进制位 来表示。

8421码又称为BCD码，是十进制代码中最常用的一种,因为代码中从左至右看每一位“1”分别代表数字“8” “4”“2”“1”，故得名8421码。

比如： 29 对应的 BCD 时（ 0010 1001 ） BCD

上分突破口3：定点数的表示形式

定点数指 小数点在数中位置固定不变的数 。定点数分为定点整数和定点小数，由于小数点位置固定

不变，所以存储时小数点不进行存储。

定点小数

定点整数

而定点数有 3 种表示法：原码、反码和补码。

原码

原码是计算机机器数中最简单的一种形式， 数值位就是真值的绝对值，符号位为“0”时表示正数，符号位为“1”时表示负数 。

11000 表示 -8

01000 表示 8

反码

反码通常是用来由原码求补码或者由补码求原码的过渡码。

规则：

原码是正数时，反码就是跟原码一样；

原码是负数时，反码就是原码符号位除外，其他位按位取反。

例子：

整数的 “+0” 原码为 0,0000000 ，反码为 0,0000000；

整数的 “-0” 原码为 1,0000000 ，反码为 1,1111111 。

补码

补码是计算机把减法运算转化为加法运算的关键编码。

规则：

正数的补码等于反码

负数的补码等于反码加一

例子：

+9 的补码是 00001001

原码是： 00001001

反码是： 00001001

-9 的补码是 11110111

原码是： 10001001

反码是： 11110110

上分突破口4：IEEE754浮点数

IEEE 浮点数标准是从逻辑上用三元组{S，E，M}来表示一个数 V 的，即：

V=（-1）S×M×2E

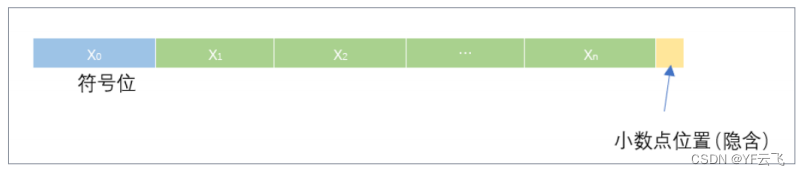
如下图所示：

其中：

符号位 s（Sign）决定数是正数（s＝0）还是负数（s＝1），而对于数值 0 的符号位解释则作为特殊情况处理。

有效数字位 M（Significand）是二进制小数，它的取值范围为 1~2-ε，或者为 0~1-ε。它也被称为尾数位（Mantissa）、系数位（Coefficient），甚至还被称作“小数”。

指数位 E（Exponent）是 2 的幂（可能是负数），它的作用是对浮点数加权。

浮点数格式是一种数据结构，它规定了构成浮点数的各个字段、这些字段的布局及算术解释。IEEE 754 浮点数的数据位被划分为三个段，从而对以上这些值进行编码。数据结构https://baike.baidu.com/item/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/1450

两种格式：

例子：

假定采用IEEE754单精度浮点数格式表示一个数为45100000H，则该数的值是( B )。

A ． (+1.125)10×210

B ． (+1.125)10×211

C ． (+0.125)10×211

D ． (+0.125)10×210